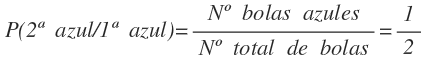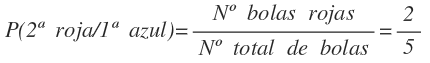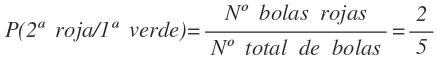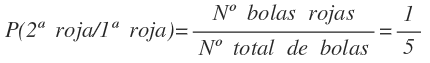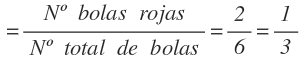A continuación te voy a explicar qué es la probabilidad condicionada, con ejercicios resueltos paso a paso. Entender qué es la probabilidad condicionada es fundamental y te servirá para resolver ejercicios de probabilidad más complejos.
¡Empezamos!
Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Qué es la probabilidad condicionada
La probabilidad de un suceso se dice que está condicionada cuando su probabilidad depende de un suceso anterior, es decir, la probabilidad del segundo suceso está condicionada al resultado del primer suceso.
Probabilidad condicionada en sucesos dependientes
La probabilidad condicionada de dos sucesos dependientes A y B se escribe P(B/A) y se lee como la probabilidad de que se realice el suceso B, habiéndose realizado el suceso A:
Por ejemplo:
Colocamos en una bolsa dos bolas azules y una bola verde. Extraemos una bola y sin devolverla a la bolsa extraemos una segunda bola (extracción sin devolución). ¿Cuál es la probabilidad de que la segunda bola extraída sea azul?
Veamos todos los casos posibles. Partimos de tener 3 bolas en la bolsa: 2 azules y 1 verde.
Si la primera bola es verde, en la bolsa nos quedan 2 bolas azules, por lo que en la segunda extracción, siempre sacaremos una bola azul. La probabilidad de que la segunda bola sea azul en este caso es de 1, ya que el número de casos favorables es el mismo que el número de casos posibles:
Si la primera bola es azul, en la bolsa nos queda 1 bola verde y 1 bola azul. En este caso, el número total de bolas es 2, pero el número de bolas azules es 1, por lo que la probabilidad es 1/2:
Como ves, en este ejemplo, la probabilidad de que la segunda bola sea azul depende del resultado de la primera extracción, por lo que la probabilidad está condicionada.
Probabilidad condicionada en sucesos independientes
Si los sucesos son independientes no existe la probabilidad condicionada.
Por ejemplo, vamos a considerar el experimento de lanzar una moneda 2 veces. La probabilidad de que salga cara (C) o de que salga cruz (X) la primera vez es de 1/2:
El resultado de lanzar otra vez la moneda, no depende para nada del resultado del primer lanzamiento, por tanto, la probabilidad de que salga cara o cruz en el segundo lanzamiento vuelve a ser de 1/2, ya que volvemos a tener 2 sucesos posibles donde solo uno de ellos es el caso favorable.
Teniendo en cuenta también el primer lanzamiento en el resultado final, las probabilidades son:
En este caso la probabilidad no está condicionada por la realización del primer suceso. En este caso, la probabilidad condicionada del segundo suceso es igual a la probabilidad del segundo suceso (independientemente de lo que pase en el primero):
Ejercicios resueltos de probabilidad condicionada
Vamos a resolver un par de ejercicios sobre probabilidad condicionada para que quede todo mucho más claro.
Ejercicio 1
Una urna contiene 2 bolas rojas, 2 verdes y 2 azules. Se saca una bola y sin devolverla a la bolsa se saca otra bola. ¿Cuál es la probabilidad de que la segunda bola sea roja…
a) …si la primera es azul?
b)… si la primera es verde?
c)… si la primera es roja?
Apartado a:
Si sacamos la primera bola azul, en la segunda extracción nos quedan 5 bolas en total, de las cuales 2 son rojas, por lo que la probabilidad es:
Apartado b:
Si la primera bola es verde, para la segunda extracción tenemos 5 bolas en total, de las cuales 2 son rojas y su probabilidad es:
Apartado c:
Si la primer bola es roja, nos quedan 5 bolas para la segunda extracción, pero esta vez sólo nos queda una bola roja. En este caso la probabilidad es:
Ejercicio 2
Una urna contiene 2 bolas rojas, 2 verdes y 2 azules. Sacamos una bola, vemos que es roja y la devolvemos a la urna antes de extraer la segunda bola. Calcula las siguientes probabilidades:
a) La segunda bola sea roja
b) La segunda bola sea verde
c) La segunda bola sea azul
En los tres casos, tenemos en primer lugar una extracción con devolución, así que no importa de qué color es la primera bola, ya que para la segunda extracción, volveremos a tener todas las bolas dentro.
En este caso los sucesos son independientes y por tanto la probabilidad de extraer al segunda bola no está condicionada por el resultado de la primera extracción.
Apartado a:
La probabilidad de que la segunda bola sea roja es igual a la probabilidad de sacar una bola roja:
Y tenemos las 6 bolas dentro de la bolsa, de las cuales 2 son rojas:
Apartado b:
Con la bola verde pasa lo mismo:
Apartado c:
Y lo mismo ocurre con la bola azul:
¿Necesitas ayuda en matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: