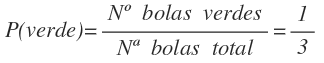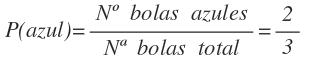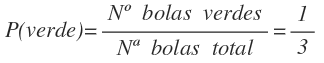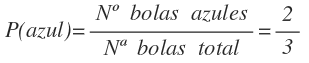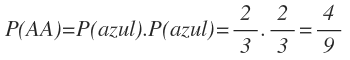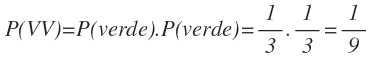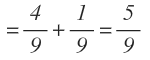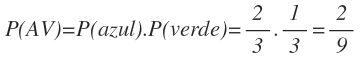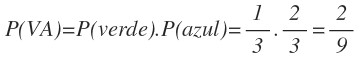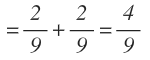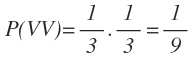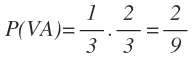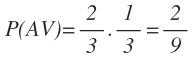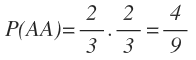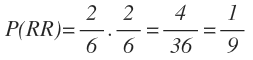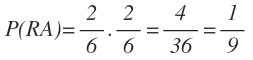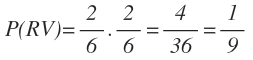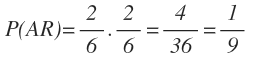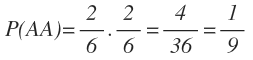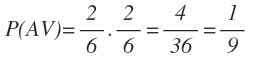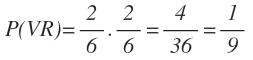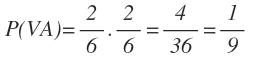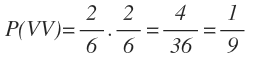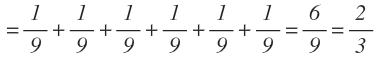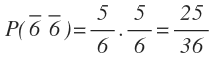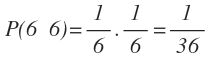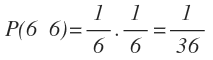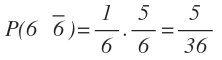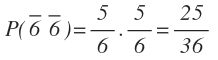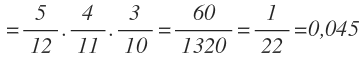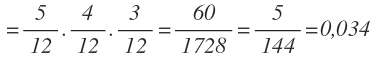En esta lección te voy a explicar qué son los sucesos compuestos independientes y cómo calcular la probabilidad de sucesos compuestos independientes, utilizando diagramas de árbol, con ejemplos y ejercicios resueltos paso a paso.
¡Empezamos!
Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Qué son sucesos compuestos independientes
Dos sucesos A y B son independientes cuando el resultado obtenido en el primer suceso A no influye en el resultado del segundo suceso B.
Por ejemplo:
En una urna tenemos 2 bolas azules y 1 verde. Extraemos una bola, anotamos el color, la devolvemos a la urna y extraemos una nueva bola.
Estos sucesos de sacar bolas con devolución son sucesos compuestos independientes, ya que el resultado de la primera extracción no influye para nada en el resultado de la segunda extracción, al devolver la bola a la urna y tener siempre las mismas bolas.
Otros ejemplos de sucesos compuestos independientes pueden ser lanzar una moneda varias veces (o varias monedas a la vez), lanzar un dado varias veces (o varios dados a la vez) y todas las extracciones con devolución o con reemplazamiento. En todos esos casos, el resultado del segundo suceso no depende del primer suceso.
Cómo calcular la probabilidad de sucesos compuestos independientes
La probabilidad de que se realicen dos sucesos independientes A y B es igual a la probabilidad que se realice el primero (A) por la probabilidad de que se realice el segundo (B), cada uno independientemente:
Si en lugar de dos sucesos independientes tenemos tres, A, B y C, entonces la probabilidad de que se realicen los tres es:
Vamos a ver un ejemplo para saber cómo calcular la probabilidad de sucesos compuestos independientes:
Vamos a utilizar el ejemplo anterior: En una urna tenemos 2 bolas azules y 1 verde. Extraemos una bola, anotamos el color, la devolvemos a la urna y extraemos una nueva bola.
a) Calcular la probabilidad de que las dos bolas sean del mismo color
b) Calcular la probabilidad de que una bola sea azul y otra verde
En la primera extracción, en la urna tenemos 2 bolas azules y 1 verde (3 bolas en total).
La probabilidad de sacar una bola verde es:
La probabilidad de sacar una bola azul es:
Para la segunda extracción, como las extracciones son con devolución, volvemos a tener las mismas bolas en la urna, por tanto, las probabilidades de sacar una bola verde o azul son las mismas que en la primera extracción.
La probabilidad de sacar una bola verde es:
La probabilidad de sacar una bola azul es:
La probabilidad de sacar dos bolas azules es igual a la probabilidad de sacar una bola azul en la primera extracción por la probabilidad de sacar otra bola azul en la segunda extracción:
De la misma forma, la probabilidad de sacar dos bolas verdes es igual a la probabilidad de sacar una bola verde en la primera extracción por la probabilidad de sacar otra bola verde en la segunda extracción:
Por tanto, la probabilidad de sacar dos bolas del mismo color será el resultado de sumar la probabilidad de sacar dos bolas azules más la probabilidad de sacar dos bolas verdes:
La probabilidad de sacar la primera bola azul y la segunda verde la calculamos multiplicando la probabilidad de sacar una bola azul en la primera extracción por la probabilidad de sacar una verde en la segunda extracción:
La probabilidad de sacar la primera bola verde y la segunda azul la calculamos multiplicando la probabilidad de sacar una bola verde en la primera extracción por la probabilidad de sacar una azul en la segunda extracción:
La probabilidad de sacar dos bolas de distinto color será igual a la probabilidad de sacar la primera bola azul y la segunda bola verde más la probabilidad de sacar la primera bola verde y la segunda azul:
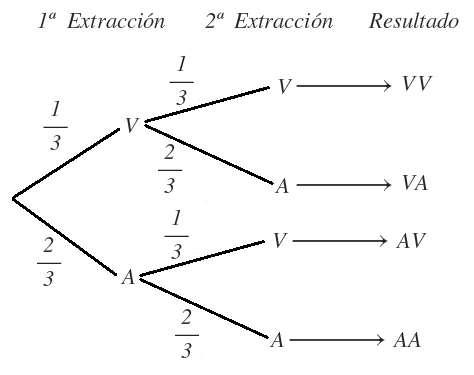
Cómo resolver problemas de problemas de probabilidad de sucesos compuestos independientes con diagrama de árbol
Vamos a ver ahora cómo resolver el ejercicio anterior con un diagrama de árbol.
Recordamos el enunciado:
En una urna tenemos 2 bolas azules y 1 verde. Extraemos una bola, anotamos el color, la devolvemos a la urna y extraemos una nueva bola.
a) Calcular la probabilidad de que las dos bolas sean del mismo color
b) Calcular la probabilidad de que una bola sea azul y otra verde
Vamos a ir construyendo el diagrama de árbol paso a paso.
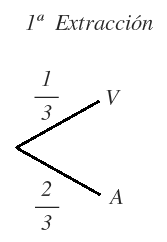
Para la primera extracción, tengo 3 bolas en total, la probabilidad de sacar una bola verde es 1/3, y la probabilidad de sacar una bola azul es 2/3 y eso lo representamos así:
Devolvemos la bola a la urna y seguimos con la segunda extracción.
Tanto si la bola fue verde o azul en la primera extracción, tengo las mismas posibilidades que al principio de sacar una bola verde o una bola azul en la segunda extracción:
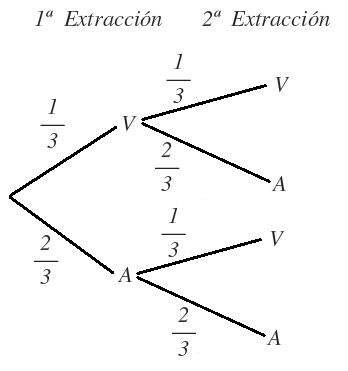
Por último, añadimos una parte más al diagrama de árbol donde recogemos todos los posibles resultados, siguiendo cada uno de los caminos:
La probabilidad de cada resultado se calcula multiplicando las probabilidades de las ramas del camino que se recorre hasta llegar hasta él.
La probabilidad de sacar dos bolas verdes la obtenemos multiplicando 1/3 de la primera rama y 1/3 de la segunda rama:
La probabilidad de sacar una primero una bola verde y después una azul la obtenemos multiplicando 1/3 de la primera rama y 2/3 de la segunda rama
La probabilidad de sacar una primero una bola azul y después una verde la obtenemos multiplicando 2/3 de la primera rama y 1/3 de la segunda rama:
La probabilidad de sacar dos bolas azules la obtenemos multiplicando 2/3 de la primera rama y 2/3 de la segunda rama:
Una vez tenemos las probabilidades de los resultados, terminamos el ejercicio igual que en el ejemplo anterior.
La probabilidad de sacar dos bolas del mismo color es:
La probabilidad de sacar dos bolas de distinto color es:
Ejercicios resueltos de probabilidad de sucesos compuestos independientes
Vamos a resolver unos ejercicios de probabilidad de sucesos compuestos independientes utilizando el diagrama de árbol.
Ejercicio 1
En una urna hay 2 bolas rojas, 2 azules y 2 verdes. Se extraen 2 bolas con reemplazamiento:
a) ¿Cuál es la probabilidad de que sean del mismo color?
b) ¿Cuál es la probabilidad de que sean de distinto color?
Realizamos el diagrama de árbol, teniendo en cuenta que para la segunda extracción tenemos las mismas probabilidades que en la primera extracción, ya que tenemos las mismas bolas en la urna:
Las probabilidades de cada resultado son:
La probabilidad de que las dos bolas sean del mismo color es:
La probabilidad de que las dos bolas sean de distinto color es:
Ejercicio 2
Se lanzan dos dados:
a) Calcula la probabilidad de que no salga ningún 6
Llamaremos 6 al suceso de sacar un 6 y un «6 con una barra encima» al suceso contrario, es decir, el suceso de no sacar un 6. Al haber 6 números en el dado, la probabilidad de sacar un 6 es 1/6 y la de no sacarlo es 5/6.
Por tanto, la probabilidad de que no salga ningún 6 es:
Siguiendo el mismo razonamiento resolvemos el resto de apartados.
b) Calcula la probabilidad de que salga un 6 en cada dado
c) Calcula la probabilidad de que el segundo sea 6, siendo 6 el primer resultado
d) Calcula la probabilidad de que el segundo no sea 6, siendo 6 el primero
e) Calcula la probabilidad de que el segundo no sea 6, no siendo 6 el primero
Ejercicio 3
En una bolsa hay 5 bolas rojas, 4 blancas y 3 negras ¿Cuál es la probabilidad de sacar la primera roja, la segunda blanca y la tercera negra?
a) Sin devolución
Para resolver este apartado, debes entender cómo calcular probabilidades de sucesos compuestos dependientes. Si lo deseas, puedes realizar previamente un diagrama de árbol para entender mejor de dónde sale cada probabilidad.
La probabilidad de que salga primero una bola roja, luego una blanca y luego una negra es:
b) Con devolución
Al hacer devolución, el número total de bolas es siempre el mismo en cada extracción. La probabilidad de sacar una bola de cada color depende del número de bolas que hay de ese color en la urna:
Al hacer la extracción con devolución, la probabilidad es menor, ya que tenemos más bolas en la urna en cada extracción que al hacerlo sin devolución.
¿Necesitas ayuda en matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: