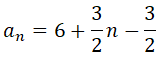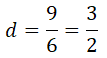A continuación veremos en que consisten las progresiones aritméticas y las fórmulas para calcular tanto su término general, su diferencia, así como la suma de los n primeros términos de una progresión aritmética.
¡Empezamos!
Si has llegado hasta aquí es porque seguramente necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolver algún ejercicio que se te resista o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Qué es una progresión aritmética
Una progresión aritmética es una sucesión donde cada término se obtiene sumando un determinado número fijo al término anterior. Ese número fijo que vamos sumando para obtener el término siguiente se llama diferencia y se representa con la letra d.
Un ejemplo de progresión aritmética es el siguiente:
Donde, si te das cuenta, cada término se obtiene sumando 2 al término anterior. Por tanto, en esta progresión aritmética, la diferencia es 2: d=2.
Aquí tenemos otra progresión aritmética:
En este caso, puede pensarse que no es una progresión aritmética, ya que los términos son cada vez menores y por tanto lo que estamos haciendo es restar en vez de sumar, pero lo cierto es que sí es una progresión aritmética, en la cual, estamos sumando un número negativo. La diferencia es -3: d=-3.
Así que, en una progresión aritmética, la diferencia puede ser tanto positiva, como negativa.
Fórmula del término general de una progresión aritmética
Como acabamos de ver, si tenemos algunos términos de una progresión aritmética, podemos conocer la diferencia y por tanto, podemos ir obteniendo los términos siguientes.
Pero, ¿qué pasa si queremos obtener un término muy elevado, como por ejemplo el término 50, de una progresión aritmética?
Sería bastante tedioso ir calculando la progresión hasta llegar al término deseado y todavía más cuando más elevado sea el término que queremos calcular.
Para evitar esto, en las progresiones aritméticas, podemos calcular el término general, que es el término en una posición n, con la siguiente fórmula:
Vamos a ver de dónde se obtiene esta fórmula para que la entiendas mejor.
Partimos de la siguiente progresión aritmética:
Para calcular el término a2, a a1 le sumamos la diferencia
Es decir, partiendo de a1, le sumamos la diferencia una vez para llegar hasta a2:
Para calcular a3, podemos sumarle a a2 la diferencia una vez:
O también podemos partir de a1 y sumarle la diferencia dos veces:
Para calcular a4 lo podemos hacer igual, es decir, podemos sumarle a a3 la diferencia:
O podemos partir desde a1 y sumar la diferencia tres veces:
Podríamos seguir así infinitas veces.
Si te das cuenta, el número por el que queda multiplicado la d cuando partimos de a1 es siempre una unidad menor que el término que queremos calcular, por ejemplo, para calcular a3, multiplicamos la d por 2, para calcular a4, multiplicamos la d por 3…
Por tanto, para calcular el término en la posición n, a a1 le sumamos la diferencia multiplicada por (n-1) veces y así es como llegamos a la fórmula del término general de una progresión aritmética:
Cómo calcular el término general de una progresión aritmética
Vamos a ver un ejemplo donde aplicar la fórmula anterior y saber cómo calcular el término general de una progresión aritmética:
Calcular el término general de la siguiente progresión geométrica:
En este caso, el primer término es igual a 2 y la diferencia también es igual a 2:
Vamos a calcular su término general aplicando la fórmula:
En primer lugar, sustituimos el término a1 y la diferencia, que son los datos que conocemos:
Ahora multiplicamos el 2 por cada uno de los términos que hay dentro del paréntesis:
Y operamos, quedándonos el término general, que va siempre en función de n:
Una vez conociendo el término general, podemos por ejemplo calcular el término que está en la posición 88, tan solo sustituyendo la n por 88 y operando:
Cómo calcular el término general de una progresión aritmética si no conocemos el primer término
Si no conocemos el primer término de una progresión aritmética, pero conocemos el valor de otro término de la progresión y la diferencia, podemos utilizar la siguiente fórmula:
donde k es la posición del término que conocemos.
Por ejemplo, en la serie anterior:
Vamos a calcular el término general, suponiendo que no conocemos el primer término y conocemos el valor del tercer término y la diferencia:
Partimos de la fórmula anterior:
Sustituimos k por 3 que es la posición que conocemos y la diferencia por 2:
Ahora sustituimos a3 por su valor:
Multiplicamos el 2 por los términos del paréntesis:
Y finalmente operamos:
Como ves, hemos llegado al mismo término general que en el caso de conocer a1.
Cómo calcular la diferencia de una progresión aritmética
Cuando conocemos dos o más términos seguidos de una progresión aritmética es bastante sencillo calcular la diferencia. Solo tenemos que restarle a un término el término anterior, o lo que es lo mismo al término en posición n, restarle el término en posición (n-1):
Pero, ¿cómo calculamos la diferencia de una progresión aritmética si no conocemos dos términos seguidos, si no que conocemos dos términos que están alternos?
Partimos de la fórmula para calcular el término general de una progresión aritmética:
De esta fórmula, podemos despejar la diferencia. Primero pasamos a1 restando al miembro contrario:
Ahora (n-1) que está multiplicando a la d, lo pasamos dividiendo al miembro contrario:
Nos queda por tanto la diferencia en función de dos términos y de la posición del termino que conocemos.
Vamos a ver un ejemplo:
Conocidos los dos términos siguientes de una progresión aritmética:
calcular el valor de la diferencia y del término general:
Partimos de la fórmula del término general de una progresión aritmética:
Sustituimos la n por 3, que es la posición que conocemos:
Ahora sustituimos a1 y a3 por sus valores:
Pasamos el 6 restando al miembro contrario:
Operamos en ambos miembros:
Despejamos d, pasando el 2 dividiendo al miembro contrario y operamos:
La diferencia es igual a 1,5.
Ahora vamos a calcular el término general:
Sustituimos a1 y d por sus valores:
Multiplicamos 3/2 por los términos del paréntesis:
Obtenemos denominador común y operamos en el numerador:
Fórmula para calcular la suma de los n primeros términos de una progresión aritmética
Vamos a ver ahora cómo sumar los términos de una progresión aritmética.
Si tenemos la siguiente progresión:
Y nos piden sumar los cuatro primeros términos, sería algo bastante sencillo:
Sin embargo, si nos piden por ejemplos sumar los 35 primeros términos, la cosa ya se complica un poco y no podemos hacer la suma de forma manual.
Para sumar los n primeros términos de una progresión aritmética, se utiliza la siguiente fórmula:
Donde n es la posición del término hasta el que queremos sumar.
Esta fórmula nos dará el resultado de sumar desde el primer término hasta el término que se encuentre en la posición n.
Por ejemplo, vamos a realizar la suma de los 35 primeros términos de la progresión anterior, es decir, la suma desde el primer término hasta el término que está en la posición 35.
Para ello aplicamos la fórmula:
Sustituimos n por 35, que es la posición hasta la que queremos calcular la suma:
Ahora en la fórmula, nos falta calcular el término a35. Para calcular este término, obtenemos primero el término general con la fórmula:
Lo hemos calculado más arriba, cuyo resultado es:
Ahora sustituimos n por 35 y obtenemos el valor de a35:
Finalmente, sustituimos el valor de a35 en la fórmula de la suma y operamos:
La suma de los 35 primeros términos es igual a 2450.
Si calculamos la suma de los cuatro primeros términos con la fórmula, verás que el resultado es el mismo que cuando lo hicimos a mano:
Ejercicios resueltos de progresiones aritméticas
Ejercicio 1
¿Qué lugar ocupa un término cuyo valor es 42 en la progresión aritmética definida por los siguientes términos?
En primer lugar, necesitamos calcular la diferencia d de al progresión aritmética.
Calcularemos la diferencia a partir de la fórmula de cómo calcular el término general de una progresión aritmética si no conocemos el primer término:
El término an debe ser mayor que el término ak:
Por lo que n debe ser mayor que k:
Por tanto, en este caso, n=9 y k=3:
Sustituimos los valores de n y k en la fórmula:
Y ahora los valores de a3 y a9 y operamos dentro del paréntesis:
Llegados a este punto vamos a despejar d. Para ello, pasamos el 6 como positivo en el segundo miembro restando al miembro contrario:
Operamos en el primer miembro:
Finalmente, pasamos el 6 que multiplica a la d, dividiendo al miembro contrario y simplificamos:
Ya conocemos cuál es la diferencia de la progresión aritmética, así como los dos términos que nos da el enunciado.
Ahora vamos a calcular la posición que ocupa un término cuyo valor es 42 en la progresión.
Para ello, volvemos a utilizar la fórmula anterior:
donde ahora, el término el cual desconocemos su posición, an, es igual a 42:
Y utilizaremos el término a3, por lo que k=3:
y por tanto, ak, será a3, que es igual a 6:
Sustituimos estos valores, así como el valor antes calculado de la diferencia en la fórmula, donde nos queda n, que es la posición que queremos calcular:
Ahora vamos a despejar n.
Empezamos multiplicando 3/2 por los dos términos del paréntesis:
Obtenemos denominador común en toda la ecuación:
Eliminamos denominadores:
Pasamos los números al primer miembro y dejamos el término con n sólo en el segundo término:
Operamos en el primer miembro:
Despejamos n pasando el 3 dividiendo al miembro contrario y operamos:
n=27, por lo que 42 corresponde al término a42 de la progresión aritmética:
Ejercicio 2
Halla la suma de todos los números impares menores que 100
Los números impares menores que 100 forman la siguiente progresión aritmética:
en la que el primer término es el 1:
Para hallar el siguiente término vamos sumando de 2 en 2, por lo que la diferencia es 2:
y el último término es 99, que es el menor número impar menor que 100.
Para hallar la suma de los números impares menores que 100, utilizaremos la fórmula:
En este caso, no sabemos a qué posición corresponde el término 99, ¿está en la posición 49? ¿en la 50?
Es decir, no conocemos n, ni en qué posición está el número 99, así que lo vamos a calcular con la fórmula del término general:
Sustituimos el término a sub n por 99, que es el término al que queremos calcular la posición n y la diferencia por su valor que es 2:
Multiplicamos en el segundo miembro para eliminar el paréntesis:
Y operamos en el segundo miembro:
Ahora vamos a despejar la n,
Empezamos pasando el -1 sumando al miembro contrario:
Sumamos en el primer miembro:
Y finalmente despejamos la pasando el 2 dividiendo al miembro contrario:
Por tanto, como n=50, ya sabemos que 99 corresponde al término que se encuentra en la posición 50, es decir, que 99 es el término a50:
Ahora, en la fórmula de la suma:
Ya podemos sustituir n por su valor:
Ya sabemos que estamos realizando la suma de los 50 primeros términos de la progresión.
Sustituimos a50 por su valor:
Y operamos:
Así que, la suma de los números impares menores que 100 es igual a 2500.
¿Necesitas ayuda en matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: