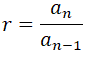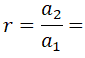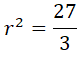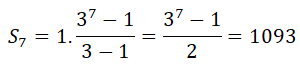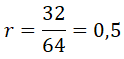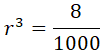A continuación vamos a ver en que consisten las progresiones geométricas y las fórmulas para calcular tanto su término general, su razón, la suma de los n primeros términos de una progresión geométrica, así como la suma de todos los términos de una progresión geométrica decreciente.
¡Empezamos!
Si has llegado hasta aquí es porque quieres aprender cómo resolver algún ejercicio que no entiendes. ¿Has pensado en apuntarte a clases de matemáticas online?. Si después de leer esto, quieres que te ayude a entender las matemáticas de verdad, puedes hacer dos cosas: o seguir buscando por Internet o suscribirte e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Qué es una progresión geométrica
Una progresión geométrica es una sucesión donde cada término se obtiene multiplicando un determinado número fijo al término anterior. Ese número fijo por el que vamos multiplicando para obtener el término siguiente se llama razón y se representa con la letra r.
Aquí tienes un ejemplo de progresión geométrica:
Si observas la progresión geométrica, cada término se obtiene multiplicando por 3 el término anterior. La razón en esta progresión geométrica es r=2.
Vamos a ver otro ejemplo:
En este caso, la progresión geométrica es decreciente. Si te fijas, cada término se obtiene dividiendo entre 2 el término anterior.
Según la definición de progresión geométrica, para obtener sus términos hay que multiplicar por un número fijo y en el ejemplo anterior estamos dividiendo, ¿es entonces una progresión geométrica?
La respuesta es que sí.
Dividir entre un número es lo mismo que multiplicar por su inverso, es decir, dividir entre 2 es lo mismo que multiplicar por 1/2, así que en el ejemplo anterior, realmente estamos multiplicando cada término por 1/2, por lo que su razón es r=1/2. También puede considerarse que r=0,5.
Por lo tanto, hay que tener en cuenta que la razón r no tiene por que ser un número positivo entero. En realidad, r puede tomar cualquier valor, tanto positivo como negativo, así como ser un número decimal.
Como consecuencia, las progresiones geométricas pueden ser crecientes o decrecientes, dependiendo del valor de r.
Fórmula del término general de una progresión aritmética
Para obtener los términos de una progresión geométrica podemos ir multiplicando por la razón hasta obtener el valor del término que queramos conocer.
Pero, si lo que queremos es saber el valor de un término cualquiera, existe una fórmula para no tener que ir calculando uno a uno y calcular el término general directamente. La fórmula a utilizar dependerá de estos dos casos:
- Cuando conocemos el primer término y la razón
- Cuando no conocemos el primer término
Veamos cada uno de ellos:
Fórmula del término general cuando conocemos el primer término y la razón
Cuando conocemos el primer término y la razón de la progresión geométrica, la fórmula para obtener su término general es la siguiente:
donde n es la posición del término que queremos calcular, an es el valor del término buscado, a1 es el valor del primer término y r es la razón de la progresión geométrica.
Para que entiendas mejor esta fórmula, vamos a ver de dónde surge.
Vamos a partir de la siguiente progresión geométrica:
Tal y como hemos visto antes, el segundo término a2, se obtiene multiplicando el primer término por la razón:
O lo que es lo mismo, partiendo de a1, multiplicamos por la razón para llegar a a2:
El tercer término, lo podemos calcular multiplicando el segundo término por la razón:
O también podemos partir de a1 y multiplicar 2 veces por la razón:
Para calcular el cuarto término, podemos multiplicar el tercer término por la razón:
O partir del primer término y multiplicar por la razón 3 veces:
Y podríamos seguir así hasta el infinito.
Si te fijas, el número por el que se eleva la r cuando partimos de a1 es siempre una unidad menor que el término que queremos calcular, por ejemplo, para calcular a3, elevamos la r a 2, para calcular a4, elevamos la r a 3…
Por tanto, para calcular el término en la posición n, multiplicamos a1 por r elevado a (n-1) veces y así es como llegamos a la fórmula del término general de una progresión aritmética:
Vamos a ver un ejemplo:
Vamos a calcular el término general de la siguiente progresión geométrica:
donde el primer término es 1 y la razón es 3:
Aplicamos la fórmula anterior:
Sustituimos a1 y r por su valores:
Una vez conocemos el término general, podemos calcular directamente cualquier término de la progresión.
Por ejemplo, vamos a obtener el valor del término que se encuentra en la posición 10. Para ello, sólo tenemos que sustituir n por 10 en la fórmula del termino general y calcular:
Fórmula del término general cuando no conocemos el primer término
Si no conocemos el primer término de la progresión geométrica, pero conocemos el valor de otro término de la progresión, así como la razón, se utiliza la siguiente fórmula:
donde k es la posición del término que conocemos.
Por ejemplo, en la progresión anterior:
Vamos a suponer que sólo conocemos el cuarto termino y la razón:
Vamos a calcular el término general partiendo de esta fórmula:
Sustituimos k por 4, que es la posición que conocemos y r por 3:
Y finalmente sustituimos a4 por su valor:
Puede parecer que el término general obtenido es distinto al del apartado anterior siendo la misma progresión, lo cual no es posible, ya que tiene que ser el mismo, pero realmente es el mismo término general.
Puedes comprobarlo obteniendo cualquier término con ambas fórmulas o también si aplicamos las propiedades de las potencias y operamos llegamos a la misma expresión del apartado anterior, es decir, expresando el 27 como 3 al cubo y luego multiplicando las potencias manteniendo la base y sumando los exponentes:
Cómo calcular la razón de una progresión geométrica
Cómo calcular la razón si conocemos dos o más términos seguidos
Si conocemos dos o más términos seguidos de una progresión geométrica, para calcular la razón, tan solo tenemos que dividir el término de una posición entre el término de la posición anterior:
Por ejemplo, en la progresión:
Para calcular la razón dividimos el segundo término entre el primero:
Cómo calcular la razón si conocemos dos términos alternos
¿Cómo calculamos la razón de una progresión geométrica si no conocemos dos términos seguidos, si no que conocemos dos términos que están alternos?
Vamos a verlo con un ejemplo.
Supongamos que solo conocemos el segundo y el cuarto término de la progresión anterior:
En este caso, para calcular la razón partimos de la fórmula del término general cuando no conocemos el primer término:
Donde siempre n debe ser mayor que k:
En nuestro caso:
Sustituimos n y k en la fórmula:
Y ahora sustituimos los valores de a2 y a4:
Me queda una ecuación en la que tengo que despejar r.
Primero paso el 3 dividiendo al miembro contrario:
Opero en el segundo miembro:
Y finalmente paso el cuadrado como raíz al miembro contrario y opero:
Fórmula para calcular la suma de los n primeros términos de una progresión geométrica
Es posible sumar directamente los n primeros términos de una progresión geométrica sin necesidad de realizar la suma manualmente, cosa que puede resultar muy tediosa si la suma de términos es muy grande.
Esta suma se realiza de con la siguiente fórmula:
donde n es la posición del término hasta el que queremos sumar, a1 es el primer término y r es la razón.
Por ejemplo, vamos a sumar los 7 primeros términos de la siguiente progresión geométrica:
Aplicamos la fórmula anterior:
donde en este caso, n=7, a1=1 y r=3:
Fórmula para calcular la suma de todos los términos de una progresión geométrica decreciente
Si la progresión geométrica es decreciente, es posible calcular la suma de todos los términos de la progresión, siempre y cuando el valor de la razón esté comprendido entre -1 y 1:
En este caso, la suma de todos los términos de la progresión geométrica es:
donde a1 es el primer término de la progresión y r es la razón,
Vamos a ver un ejemplo: Calcular la suma de todos los términos de la siguiente progresión
En primer lugar obtenemos la razón dividiendo el segundo término entre el primero:
El valor de r está entre -1 y 1 por lo que se puede realizar la suma.
Sustituimos a1 y r por sus valores y operamos:
Todos los términos de la progresión suman 128.
Ejercicios resueltos de progresiones geométricas
Ejercicio 1
Calcula la suma de los cinco primeros términos de una progresión geométrica en la que tenemos los siguientes términos:
¿Se puede hallar la suma de sus infinitos términos?
Para calcular la suma de los cinco primeros términos utilizamos la siguiente fórmula:
pero antes, para poder calcular la suma, antes debemos obtener la razón de la progresión geométrica.
La razón la obtenemos a partir de la fórmula para calcular el término general:
Donde en nuestro caso, a1 lo conocemos y como también conocemos que el término a4, podemos sustituir n por 4:
La fórmula nos queda:
Ahora sustituimos a1, a4 por sus valores y operamos en el exponente:
Ahora ya podemos despejar r. Primero pasamos el 1000 dividiendo al miembro contrario:
Después pasamos el cubo como raíz cúbica el miembro contrario:
Resolvemos la raíz cúbica mediante las propiedades de las raíces, expresando la raíz cúbica de la fracción como un cociente de raíces cúbicas, resolviendo las raíces y operando el cociente que nos queda:
Por tanto, la razón de la progresión geométrica es igual a 0,2.
Ahora ya podemos calcular la suma de los cinco primeros términos.
Sustituimos n por 5 en la fórmula de la suma:
Sustituimos a1 y r por sus valores y operamos:
Como la progresión es decreciente y r es mayor que -1 y menor que 1, es posible sumar los infinitos términos de la progresión geométrica con la siguiente fórmula:
Sustituimos a1 y r por sus valores y operamos:
¿Necesitas ayuda en matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: