A continuación te voy a explicar cómo representar puntos, rectas y planos en el sistema diédrico cuando estos elementos están definidos por coordenadas. Lo veremos con ejercicios resueltos paso a paso.
¡Empezamos!
Si has llegado hasta aquí es no entiendes el sistema diédrico y es muy probable que necesites clases de sistema diédrico online. Si después de leer esto, quieres seguir aprendiendo paso a paso y desde cero, en una plataforma donde tengas todo explicado, con ejercicios resueltos y alguien que te resuelva tus dudas, solo tienes que apuntarte al Curso de Sistema Diédrico Online:
VER CURSO DE SISTEMA DIÉDRICO ONLINE
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar sistema diédrico. Puedo explicarte paso a paso cualquier duda que no entiendas.
Sólo tienes que dejarte guiar y verás como vas a aprendiendo poco a poco a resolver tus ejercicios de sistema diédrico.
Representación de puntos por coordenadas en el sistema diédrico
En el sistema diédrico, podemos representar un punto el cual, esté definido por coordenadas, de la forma P (x,y,z), donde x, «y» y z son las coordenadas del punto.
Para saber cómo representar un punto definido por coordenadas en el sistema diédrico, debemos conocer dónde se encuentran los ejes de coordenadas y a qué corresponde cada una de las coordenadas del punto en el sistema diédrico.
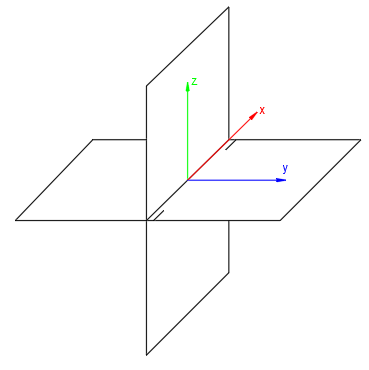
Como vemos en este esquema, el eje x se encuentra en línea de tierra, el eje y está en el plano de proyección horizontal y el eje z en el plano de proyección vertical.
Coordenadas de un punto en el sistema diédrico
Para poder situar cada una de las coordenadas en el sistema diédrico, antes necesitamos un punto de origen O, que puede estar situado en un extremo de la línea de tierra o en cualquiera de sus puntos. Este punto de origen, no lo puede dar el ejercicio o podemos definirlo nosotros.
En este caso, lo vamos a situar por ejemplo en el centro de la línea de tierra:
Una vez tenemos el origen, ya podemos situar cada una de las coordenadas del punto x, y, z. Vamos a ver a qué corresponde cada una de ellas.
La coordenada x hace referencia al desplazamiento en la línea de tierra. Si es positivo nos movemos a la derecha del origen y si es negativo nos movemos hacia la izquierda:
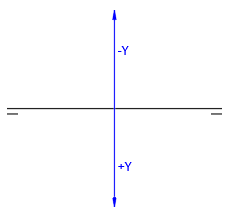
La coordenada y hace referencia al alejamiento del punto. Los alejamientos son positivos por debajo de la línea de tierra y negativos por encima de la línea de tierra. En esta coordenada es donde se coloca la proyección horizontal del punto:
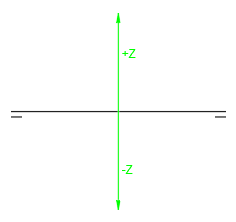
Por último, la coordenada z corresponde a la cota del punto, siendo positiva cuando está por encima de la línea de tierra y negativa cuando está por debajo. En esta coordenada es donde se coloca la proyección vertical del punto:
Ejercicios resueltos de representación de puntos por coordenadas en diédrico
Vamos a resolver algunos ejercicios de representar puntos que están definidos por coordenadas en el sistema diédrico.
Ejercicio 1
Por ejemplo, vamos a representar el punto A (2, 5, 1).
En primer lugar, definimos el origen, que en mi caso lo situaré en el centro de la línea de tierra:
Empezamos situando la coordenada x, que es igual a 2. Recordamos que esta coordenada se mueve en la dirección de la línea de tierra. Como es positivo, nos movemos 2 unidades hacia la derecha:
La amplitud de las unidades puedes ser cualquiera. Pueden ser centímetros o cualquier otra unidad que estimes oportuna. Eso sí, debe ser la misma para los tres ejes. En vez de dibujar unidades como estoy haciendo yo, también puedes medir las unidades directamente con el compás o con la regla. Yo lo hago así para que se vean bien y entiendas lo que voy haciendo.
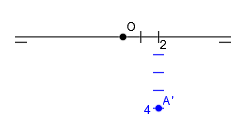
Seguimos con la coordenada y, que en este caso es igual a 4. Como es positiva, nos movemos 4 unidades hacia abajo desde el punto x=2 de la línea de tierra. En este punto situamos la proyección horizontal del punto A’:
Para situar la coordenada z, igual a 1, como es positiva, nos movemos 1 unidad hacia arriba desde el punto x=2 de la línea de tierra. En este punto situamos la proyección vertical del punto A’ ‘:
Por tanto, el punto A (2,4,1) queda representado de la siguiente manera, donde 4 es el alejamiento del punto y 1 su cota:
Ejercicio 2
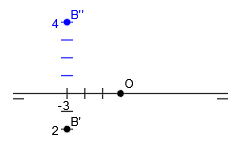
Vamos a ver otro ejemplo. Vamos a representar el punto B (-3, 2, 4).
Empezamos situando el punto de origen:
En este caso, x es igual a -3, luego nos movemos 3 unidades a la izquierda del origen en la línea de tierra:
Seguimos con la coordenada y, que es igual a 2, luego nos movemos 2 unidades hacia abajo desde el punto x=-3 y situamos la proyección B’:
Por último, z=4. Nos movemos 4 unidades hacia arriba desde x=-3 en la línea de tierra, situando aquí la proyección vertical del punto B’ ‘:
Por tanto, el punto B (-3, 2, 4) nos queda:
Ejercicio 3
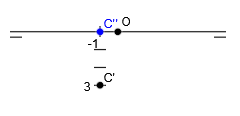
Representar el punto C (-1, 3, 0).
Situamos el origen:
x=-1, luego nos movemos 1 unidad hacia la izquierda del origen en la línea de tierra:
Para situar la coordenada y, que es igual a 3, nos movemos 3 unidades hacia abajo de la línea de tierra desde x=-1 y es aquí donde colocamos X’:
La coordenada z es 0, luego quiere decir que la proyección vertical del punto se queda en la línea de tierra:
El punto C (-1, 3, 0) queda representado de la siguiente forma:
Ejercicio 4
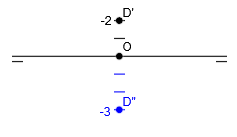
Representar el punto D (0, -2, -3)
Situamos el origen en la línea de tierra. Como x=0, coincide con el origen:
En este caso y=-2, luego nos movemos 2 unidades hacia arriba y situamos la proyección horizontal D’:
z=-3, que al ser negativa, nos movemos 3 unidades hacia abajo desde la línea de tierra y es donde colocamos D’ ‘:
El punto D (0, -2, -3) nos queda:
Representación de rectas por coordenadas en el sistema diédrico
Vamos a ver ahora cómo representar rectas definidas por coordenadas en el sistema diédrico.
Para definir una recta por coordenadas, debemos definir por coordenadas dos puntos que pertenezcan a la recta y después unir dichos puntos.
Vamos a ver un ejemplo.
Vamos a representar la recta que pasa por los puntos A (2,4,1) y B (-3, 2, 4).
En primer lugar definimos el origen:
Representamos ambos puntos (que ya los hemos representado más arriba):
Finalmente, unimos A’ y B’ para obtener r’ y A’ ‘ y B’ ‘ para obtener r’ ‘:
Representación de rectas por coordenadas a partir de sus trazas
También podemos representar una recta si tenemos las coordenadas de sus trazas.
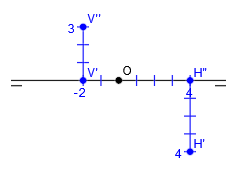
Por ejemplo vamos a representar la recta que pasa por la traza horizontal H (4,4,0) y por la traza vertical V (-2,0,3).
Empezamos situando el origen:
Representamos H y V siguiendo los pasos que he explicado más arriba:
Y por último, unimos H’ y V’ para obtener r’ y H’ ‘ y V’ ‘ para obtener r’ ‘:
Cómo representar planos por coordenadas en el sistema diédrico
Por último, te voy a explicar cómo representar planos que estén definidos por coordenadas en el sistema diédrico, es decir planos definidos de la forma α (x, y, z), donde x, «y» y z son las coordenadas del plano.
La correspondencia de cada coordenada coincide con las coordenadas del punto:
- La coordenada x hace referencia al desplazamiento en la línea de tierra. Si es positivo nos movemos a la derecha del origen y si es negativo nos movemos hacia la izquierda. En este punto se encontrará el vértice del plano.
- La coordenada y hace referencia al alejamiento. Es positiva hacia abajo desde la línea de tierra y negativa por encima de la línea de tierra. La traza horizontal del plano pasa por este punto y por el vértice (coordenada x).
- La coordenada z corresponde a la cota, siendo positiva cuando está por encima de la línea de tierra y negativa cuando está por debajo. La traza vertical del plano pasa por este punto y por el vértice (coordenada x).
A diferencia con la representación de los puntos, en los planos, las coordenadas «y» y z se representan siempre desde el origen, no desde la coordenada x como se hace en los puntos.
Por tanto, una vez que tenemos representadas las tres coordenadas, sólo tenemos que unir la coordenada x con las otras dos coordenadas para obtener las trazas del plano.
Vamos a ver cómo representar un plano por coordenadas en diédrico paso a paso con un ejemplo resuelto. Vamos a representar el plano α (2, 4, 3).
Primero definimos el origen:
Ahora situamos la coordenada x, que como es positiva, se encuentra a 2 unidades a la derecha del origen:
Este punto será el vértice del plano.
Para situar la coordenada «y», desde el origen de coordenadas, nos movemos 4 unidades hacia abajo, ya que es positiva:

La coordenada z, la situamos moviéndonos hacia arriba 3 unidades, también desde el origen:
Para terminar dibujamos la traza vertical del plano α2, uniendo el vértice, que está en x=2 en la línea de tierra, con la coordenada «z»:
Representación de planos con alguna coordenada negativa
Vamos a ver otro ejemplo, en el que alguna de las coordenadas sea negativa. Vamos a representar el plano α (2,-3,1).
Situamos el origen:
Representamos la coordenada x:
La coordenada «y», como es negativa, la situamos 3 unidades por encima de la línea de tierra:
En este caso, para representar la traza horizontal α1, unimos el vértice que está en x=2, con y=-3 y después prolongamos la traza por debajo de la línea de tierra. La parte que queda por encima de la línea de tierra se representa en discontinuo, ya que no se encuentra en el primer cuadrante:
Representamos la coordenada z:
Y unimos x=2 con z=1 para representar la traza vertical α2:
Si la coordenada z fuera negativa, se procedería de forma análoga que con la coordenada «y». Si la coordenada x fuera negativa, solo influye en que el vértice se encontraría a la izquierda del origen.
Representación de planos con alguna coordenada igual a infinito
Vamos a ver cómo representar planos cuando alguna de su coordenada es igual a infinito.
Si la coordenada x es la que vale infinito, las dos trazas del plano serán paralelas la línea de tierra. La coordenada «y» marca la distancia entre α1 y la línea de tierra y la coordenada «z» marca la distancia entre α2 y la línea de tierra.
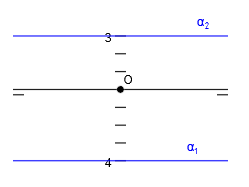
Por ejemplo, si representamos el plano α (∞, 4, 3), nos queda de la siguiente forma, donde desde α1 a la línea de tierra hay 4 unidades y desde α2 hasta la línea de tierra hay 3 unidades:
Si la coordenada «y» es la que vale infinito, entonces la traza horizontal del plano es perpendicular a la línea de tierra, o dicho de otra forma, será un plano proyectante de plano vertical.
Por ejemplo, si representamos el plano α (2, ∞, 3), nos queda de la siguiente manera:
Si la coordenada «z» es la que vale infinito, entonces la traza vertical del plano es perpendicular a la línea de tierra, es decir, representaremos un plano proyectante de plano horizontal.
Por ejemplo, el plano α (2, 4, ∞) queda representado de la siguiente manera:
¿Necesitas clases de sistema diédrico? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para entender cualquier concepto de sistema diédrico.
He diseñado un método práctico y efectivo que te ayudará a entender cómo resolver ejercicios de sistema diédrico, paso a paso, explicándote justo lo que necesitas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios de sistema diédrico y lo más importante, sabrás por qué se dan esos pasos.
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando información por Internet si puedes aprenderlo en menos de 20 minutos?
Te explicaré lo que necesitas aprender para entender el sistema diédrico. ¿Quieres informarte de como puedes aprender sistema diédrico? Pulsa el botón para saber más:
VER CURSO DE SISTEMA DIÉDRICO ONLINE