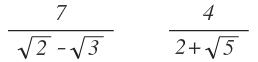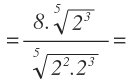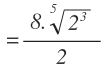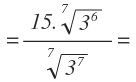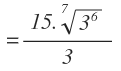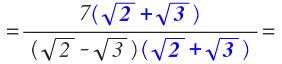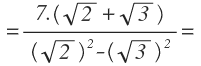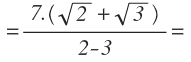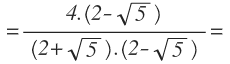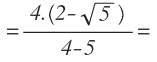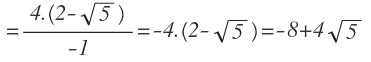¿Sabes qué es racionalizar? RACIONALIZAR RADICALES consiste en eliminar las raíces del denominador.
Para deshacernos de las raíces del denominador, evidentemente no basta con quitarlas de ahí, ya que modificaríamos el resultado de la expresión. Hay que encontrar una expresión equivalente a la original pero sin raíces en el denominador.
¿Y eso como hacemos eso? Pues vamos a verlo
Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Cómo racionalizar radicales en expresiones con radicales en el denominador
Tenemos dos casos en los que podemos racionalizar radicales, es decir, eliminar los radicales del denominador:
1- Cuando en el denominador tenemos una sola raíz (no importa el índice), como por ejemplo éstas expresiones:
2- Cuando en el denominador hay una suma o resta en el que un término o los dos sea una raíz CUADRADA, como por ejemplo:
Vamos a ver con todo detalle y paso a paso, cómo racionalizar radicales en cada uno de ellos.
Cómo racionalizar radicales en expresiones con una raíz en el denominador
Para racionalizar radicales cuando sólo tengamos una raíz en el denominador, vamos a eliminarla aplicando la siguiente propiedad:
Es decir, tenemos que conseguir que la raíz se anule y para ello debemos hacer que el exponente sea igual que el índice.
Para conseguirlo, tenemos que multiplicar la raíz del denominador, por otra raíz, tal que al multiplicarlas, su resultado sea otra raíz que se anule. Y para no modificar el resultado, se multiplica el numerador por la misma raíz.
Para ello, debes tener en cuenta que:
- Las raíces deben tener el mismo índice para poderlas multiplicar
- Al multiplicar dos potencias con la misma base, se suman los exponentes
- El exponente del radicando de la nueva raíz, debe complementarse con el exponente del radicando de la raíz actual, para que su suma sea igual al índice de las raíces
Vamos a verlo más despacio con un ejemplo:
Para empezar a eliminar la raíz del denominador, la multiplicamos por otra que tenga el mismo índice:
El radicando de la nueva raíz, debe ser una potencia con la misma base que la raíz actual:
Y su exponente, debe ser tal, que al sumarlo con el exponente de la raíz actual, su resultado sea igual al índice. Es decir, el exponente del radicando de la raíz actual es 2 y queremos otro exponente (x) que al sumarlo, el resultado sea 5, por tanto, ese exponente será 3:
Y lo colocamos en la nueva raíz:
Ahora que hemos obtenido la raíz por la que tenemos que multiplicar el denominador, para no modificar el resultado de la expresión, debemos multiplicar también el numerador:
Y a partir de aquí, empezamos a realizar la multiplicación en el denominador. En primer lugar, unimos las dos raíces en una:
Multiplicamos las potencias, manteniendo la base y sumando los exponentes:
Y finalmente, la raíz se anula con el exponente del radicando, que era lo que estábamos buscando desde el principio:
Vamos a ver otro ejemplo de racionalizar radicales, para que te quede aún más claro:
En primer lugar, multiplicamos por una raíz con el mismo índice:
Dentro de la nueva raíz, la potencia debe tener la misma base:
Y su exponente resulta de restar el índice menos el exponente del radicando de la raíz actual:
Multiplicamos también el numerador por la raíz obtenida:
Y empezamos a multiplicar las raíces en el denominador, unificándolas en una sola raíz:
Ahora multiplicamos las potencias que tenemos dentro de la nueva raíz, manteniendo la base y sumando los exponentes:
Y finalmente se anula la raíz del denominador:
Voy a pasar a explicarte ahora el segundo caso de racionalizar radicales.
Cómo racionalizar radicales en expresiones con una suma o resta de raíces en el denominador
El segundo caso de racionalizar radicales consiste, como te he indicado al principio de la lección, en que en el denominador tenemos una suma o una resta de dos términos, donde al menos uno de ellos es una raíz cuadrada.
Es muy importante remarcar que sea raíz cuadrada, ya que si tiene otro índice, este procedimiento no sería válido y no podría racionalizarse.
Como en el caso anterior, tenemos que eliminar las raíces, pero esta vez lo haremos con la ayuda de la propiedad de que una suma por una diferencia es igual a la diferencia de cuadrados:
Para ello, tenemos que multiplicar el numerador y el denominador por el conjugado del denominador.
Para obtener el conjugado de una suma o de una resta (de un binomio), tan sólo tenemos que cambiar el signo central. Por ejemplo, el conjugado de:
Sería respectivamente:
Como ves, sólo hemos cambiado el signo central.
Sabiendo esto, vamos a explicar un ejemplo paso a paso:
Para racionalizar radicales en esta expresión, multiplicamos el numerador y el denominador por el conjugado del denominador, que lo hemos obtenido cambiándole el signo menos por un signo más:
Ahora aplicamos la propiedad de la diferencia de cuadrados en el denominador:
Y resolvemos los cuadrados:
Como has visto, al elevar las raíces al cuadrado, se han anulado, que era lo que buscábamos, por eso, este procedimiento sólo es válido con raíces cuadradas.
Ahora sin raíces, seguimos operando para simplificar la expresión:
Vamos con otro ejemplo:
Empezamos multiplicando el numerador y el denominador por el conjugado del denominador:
Aplicamos el producto notable de la diferencia de cuadrados en el denominador;
Resolvemos los cuadrados y se anula el término que tenía la raíz:
Y ahora operamos para simplificar la expresión:
¿Necesitas ayuda con las matemáticas? ¿Quieres que te explique cualquier duda que te surja paso a paso?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: