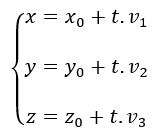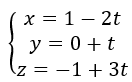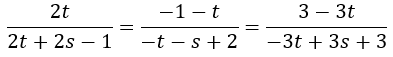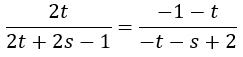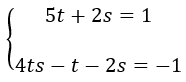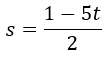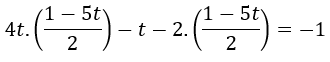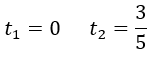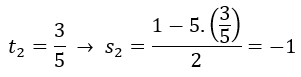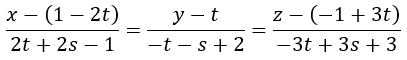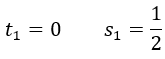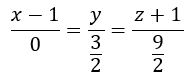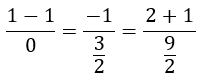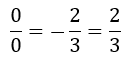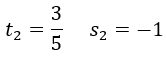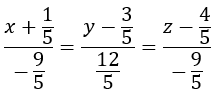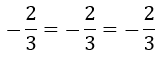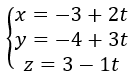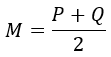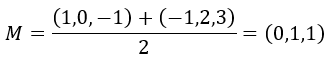Vamos a ver cómo obtener una recta que se apoya en otras dos rectas dadas y que pase por un punto punto fijo, con ejercicios y ejemplos resueltos paso a paso.
¡Empezamos!
Si has llegado hasta aquí es porque necesitas un profesor de matemáticas online. Si después de leer esto, quieres que te ayude a entenderlas de verdad, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Cómo obtener una recta que se apoye en otras dos rectas dadas
Antes de empezar a explicar cómo calcular la ecuación de una recta que se apoye sobre otras dos rectas dadas, debemos saber qué es una recta que se apoya sobre otras dos rectas.
Así que, ¿qué es una recta que se apoya sobre otras dos rectas? Pues es una recta que corta al mismo tiempo a otras dos rectas, de las cuales conocemos su ecuación.
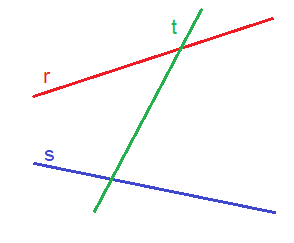
Por ejemplo, la recta t, se apoya en las rectas r y s, ya que corta a las rectas r y s:
Para obtener la ecuación de una recta que se apoye sobre otras dos rectas dadas, debemos tomar un punto genérico de cada recta, que tendrá por coordenadas las mismas que las ecuaciones paramétricas de la recta.
Sabemos que si conocemos un punto P0 perteneciente a la recta y su vector de dirección:
Las ecuaciones paramétricas de la recta en el espacio son:
Y por tanto, las coordenadas de un punto genérico de la recta son:
Una vez hallados los puntos genericos de cada recta, P1 y P2, obtenemos el vector formado por dichos puntos:
La recta que se apoya sobre otras dos, tendrá como punto perteneciente a ella P1 (o P2 también podria ser) y su vector de dirección será el vector formado por los puntos genéricos P1 y P2:
Ejemplo de cómo calcular la ecuación de una recta que se apoye en otras dos rectas dadas
Vamos a ver un ejemplo de cómo calcular la ecuación de una recta que se apoye en otras dos rectas dadas, aplicando lo explicado en el apartado anterior.
Tenemos las ecuaciones de las rectas r1 y r2:
A partir de la ecuación de la recta r1:
Obtenemos las coordenadas del punto por donde pasa y de su vector de dirección:
Sus ecuaciones paramétricas son:
Las coordenadas de un punto genérico de la recta r1 son:
A partir de la ecuación de la recta r2:
Obtenemos también las coordenadas del punto por donde pasa y de su vector de dirección:
Las ecuaciones paramétricas de la recta r2 son:
Siendo las coordenadas de un punto genérico de la recta r2:
Una vez tenemos las coordenadas de los puntos genéricos P1 y P2, obtenemos el vector formado por dichos puntos, restando las coordenadas del origen (P1) a las coordenadas del extremo (P2):
Operamos y nos queda:
La recta que se apoya sobre r1 y r2, pasa por el punto P1 y su vector de dirección es el vector formado por los puntos genéricos P1 y P2:
Su ecuación continua queda de la siguiente forma:
Ésta es la ecuación de la recta que se apoya sobre las rectas dadas r1 y r2, que queda en función de los parámetros t y s.
Cómo obtener la ecuación de una recta que se apoya en otras dos y pasa por un punto
Vamos a ver ahora cómo obtener la ecuación de una recta que se apoya en otras dos y pasa por un punto P. Para ello, obligaremos a que el punto P pertenezca a la recta que se apoya, obteniendo los valores de t y s que hagan posible esta condición.
Vamos a verlo paso a paso.
Tenemos las ecuaciones de las rectas r1 y r2, las mismas que en el apartado anterior:
La ecuación continua de la recta que se apoya sobre r1 y r2, obtenida en el aparatado anterior, en función de los parámetros t y s es:
Ahora vamos a obligar que esta recta pase por el punto P:
Para ello, en la ecuación anterior, sustituimos x, y y z por las coordenadas del punto P:
Operamos y nos queda:
Ahora vamos a obtener los valores de t y s que verifican esta ecuación.
Para ello, igualamos los miembros de la ecuación dos a dos y obtenemos un sistema de ecuaciones cuyas incógnitas son t y s:
Para resolver este sistema, antes vamos a simplificar las ecuaciones.
Simplificamos la primera ecuación:
Multiplicamos en cruz:
Eliminamos paréntesis:
Agrupamos términos semejantes y reordenamos:
Simplificamos la segunda ecuación:
Multiplicamos en cruz:
Eliminamos paréntesis:
Agrupamos términos semejantes y reordenamos:
Simplificamos dividiendo toda la ecuación entre 3:
El sistema nos queda, el cual pasamos a resolver:
De la primera ecuación:
Despejamos s:
En la segunda ecuación:
Sustituimos s por la expresión obtenida anteriormente:
Operamos para eliminar paréntesis:
Eliminamos denominadores:
Agrupamos términos semejantes y reordenamos:
Simplificamos dividiendo la ecuación entre 4:
Las soluciones de esta ecuación son:
Para cada valor de t, obtenemos su correspondiente valor de s, sustituyendo el valor de t en la expresión donde despejamos la s:
Hemos obtenido dos pares de soluciones de t y s, los cuales sustituiremos en la ecuación de la recta en función de t y s, para obtener la ecuación de la recta final.
Recordamos sa ecuación continua de la recta que se apoya sobre r1 y r2, expresada en función de los parámetros t y s:
Sustituimos el primer par de soluciones en la ecuación:
Operamos y nos queda una ecuación de la recta que se apoya en r1 y r2 y pasa por el punto P:
Vamos a comprobar que el punto P pertenece a la recta:
Sustituimos x, y y z por las coordenadas del punto P:
Operamos y nos queda:
En el primer miembro nos queda una indeterminación y en el segundo y tercer miembro no se cumple la igualdad. Entonces, el punto P no pertenece a la recta y por tanto, la ecuación anterior no es solución del problema.
Sustituimos ahora el segundo par de soluciones en la ecuación:
Operamos y nos queda una ecuación de la recta que se apoya en r1 y r2 y pasa por el punto P:
Comprobamos que el punto P pertenece a la recta, sustituyendo las coordenadas del punto en la ecuación:
Operamos y nos queda:
En este caso, el punto P sí pertenece a la recta. Por tanto, la ecuación de la recta que se apoya en r1 y r2 y pasa por el punto P es:
Ejercicio resuelto sobre una recta que se apoya en otras dos y pasa por un punto
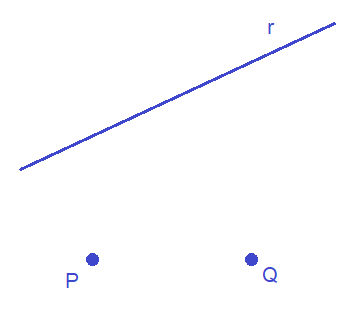
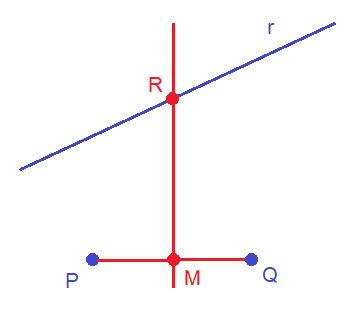
Dados los puntos P y Q:
encuentra un punto R de la recta r cuya ecuación es:
que verifique que el triángulo de vértices P, Q y R sea isósceles, siendo PQ la base.
Antes de empezar a hacer cálculo, vamos a realizar un esquema de lo que vamos a hacer. Tenemos los puntos P y Q y la recta r:
Vamos a obtener las coordenadas del punto R, perteneciente a la recta r, como punto genérico de la recta que se apoya sobre r y por la recta que pasa por P y Q, cuyo punto genérico sobre esa recta coincidirá con el punto medio M de esos dos puntos:
Como la recta que pasa por M y R es perpendicular a la recta que pasa por P y Q, se tiene que cumplir que el producto escalar de sus vectores de dirección tiene que se igual a cero:
condición que nos servirá para obtener el valor del parámetro t y encontrar así las coordenadas del punto R.
Empezmoa obteniendo las coordenadas del punto R, como punto genérico de la recta r. Para ello, obtenemos las ecuaciones paramétricas de la recta r:
Las coordenadas del punto genérico R son:
Obtenemos ahora las coordenadas del punto M, como punto medio de los puntos P y Q:
Como las rectas PQ y MR son perpendiculares, el producto escalar de sus vectores de dirección tiene que se igual a cero:
Obtenemos el vector PQ:
Obtenemos el vector MR:
Realizamos el producto escalar de los vectores PQ y MR y lo igualamos a cero:
Eliminamos paréntesis:
Agrupamos términos semejantes y reordenamos:
Y despejamos t:
Finalmente, en las coordenadas del punto genérico R:
Sustituimos t por su valor:
Y operamos, obteniendo las coordenadas de R que cumplen las condiciones del enunciado:
¿Necesitas ayuda en matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: