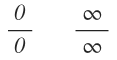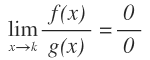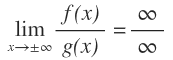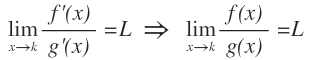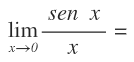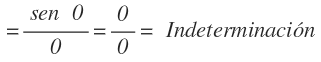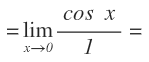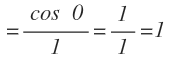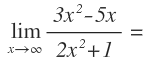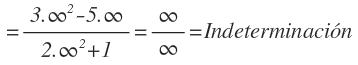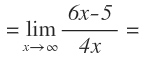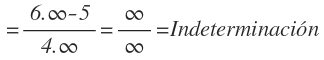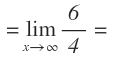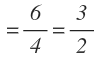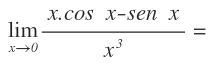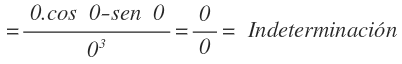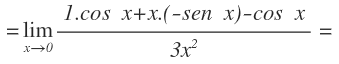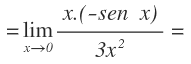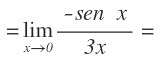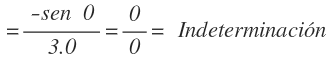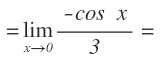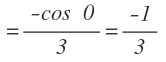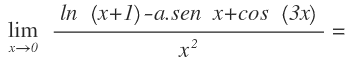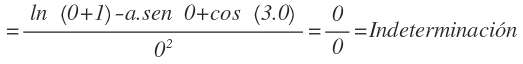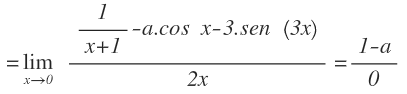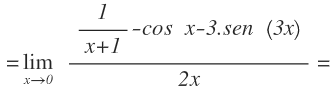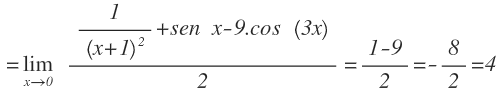A continuación voy a explicarte cómo resolver límites con la regla de L’Hôpital. Veremos en qué casos se utiliza y cómo aplicarla con ejercicios resueltos paso a paso.
Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Cuándo se usa la regla de L’Hôpital
La regla de L’Hôpital se usa directamente para resolver las indeterminaciones cero entre cero e infinito entre infinito:
Utilizamos esta regla cuando no es posible resolver los límites con otros métodos o para simplificar los cálculos.
Indirectamente podemos utilizar la regla de L’Hôpital con estos tipos de indeterminaciones: infinito menos infinito, cero por infinito, cero elevado a cero, uno elevado a infinito e infinito elevado a cero, ya que durante su método de resolución se reducen a las dos indeterminaciones anteriores (cero entre cero e infinito entre infinito):
Nos vamos a centrar sólo en resolver límites con indeterminaciones cero entre cero e infinito entre infinito para resolverlas mediante la regla de L’Hôpital.
En qué consiste la regla de L’Hôpital
La regla de L’Hôpital consiste en que si tenemos el límite de una función racional, donde tanto el numerador como el denominador son funciones, es decir, funciones que tengan esta forma:
podemos derivar la función del numerador por un lado y el denominador por otro, con lo que eliminaremos la indeterminación y obtendremos una nueva función racional, cuyo límite será igual al límite de la función original:
Es decir, para aplicar la regla de L’Hôpital, tan sólo tenemos que derivar en el numerador y en el denominador hasta que al sustituir por el número al que tiende el límite, tengamos una solución finita.
Mucho cuidado, ya que la función del numerador y la función del denominador se derivan como si fueran funciones independientes la una de la otra. No es correcto derivar la función como una división de funciones.
Si necesitas repasar cómo derivar, lo tienes explicado en el Curso de Derivadas.
Vamos a verlo con unos cuantos ejercicios resueltos para que te quede todo más claro.
Ejercicios resueltos de límites por la regla de L’Hôpital
Vamos a resolver límites de funciones con la regla de L’Hôpital paso a paso para que aprendas cómo es el procedimiento.
Ejercicio 1
Empezamos como cualquier límite, sustituyendo la x por el 0 y llegamos a la indeterminación cero entre cero:
Aplicamos L’Hôpital, derivando en el numerador por un lado y derivando en el denominador por otro y nos queda:
Volvemos a sustituir la x por el cero y obtenemos la solución final:
Ejercicio 2
Sustituimos la x por infinito y llegamos a la indeterminación infinito entre infinito:
Lo podríamos resolver por el método para resolver límites con la indeterminación infinito entre infinito, pero lo vamos a resolver aplicando L’Hôpital. Para ello, derivamos las funciones que tenemos en el numerador y en el denominador:
Volvemos a sustituir la x por infinito y nos vuelve a queda la indeterminación infinito entre infinito:
Volvemos a aplicar la regla de L’Hôpital y derivamos el numerador y el denominador:
Ahora las x han desaparecido, por lo que directamente el resultado es la función del límite, que pasamos a simplificar:
Como ves, no siempre tenemos el resultado del límite aplicando una vez la regla de L’Hôpital. Hay aplicarla y sustituir la x por el número al que tiende hasta que desaparezca la indeterminación.
Ejercicio 3
Empezamos sustituyendo la x por el cero y llegamos a la indeterminación cero entre cero:
Aplicamos la regla de L’Hôpital. Para ello, derivamos el numerador y derivamos el denominador:
Operamos en el numerador y desaparece el coseno de x:
Ahora, seguimos operando, ya que podemos eliminar una x del numerador y del denominador:
Volvemos a sustituir la x por el cero y nos vuelve a quedar la indeterminación cero entre cero:
Aplicamos otra vez la regla de L’Hôpital:
Sustituimos la x por el cero y esta vez sí que llegamos a la solución:
Ejercicio 4
Sabiendo que el siguiente límite es finito, calcula «a» y el valor del límite:
En primer lugar sustituimos la x por 0, llegando a la indeterminación 0/0:
Aplicamos la regla de L’Hôpital y volvemos a sustituir la x por 0
El enunciado nos dice que este límite es finito, por lo que deberíamos llegar al resultado siguiendo aplicando la regla de L’Hôpital. Para ello, al sustituir la x por 0, debemos llegar a la indeterminación 0/0, por lo que el numerador debe ser igual a 0:
Sabiendo esto despejamos «a», que es igual a 1.
Una vez sabemos el valor de «a», lo sustituimos en el límite:
Y seguimos resolviendo aplicando la regla de L’Hôpital:
Hay veces que no queda más remedio que utilizar la regla de L’Hôpital para resolver límites con estos tipos de indeterminaciones y otras podrás elegir el método. Puede que simplifiques los cálculos o puede que el tiempo en desarrollar los cálculos sea similar. En cualquier caso, si puedes elegir el método, elige aquel con el que te sientas más cómodo.
Te dejo ahora que practiques con los siguientes ejercicios propuestos.
Ejercicios propuestos
Calcula los siguientes límites aplicando la regla de L’Hôpital:
Si quieres aprender a resolver todos los límites sin dudar ni un momento, te recomiendo el Curso de Límites, en el que tienes lecciones explicadas desde el principio paso a paso, con muchos ejercicios resueltos y propuestos para practicar.
¿Necesitas ayuda con las matemáticas? ¿Quieres que te explique cualquier duda que te surja paso a paso?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más:
Exámenes resueltos de Matemáticas II Selectividad (PBAU) Baleares
Exámenes resueltos de Matemáticas II Selectividad (ABAU) Galicia
Exámenes resueltos de Matemáticas II Selectividad (EBAU) Castilla y León
Exámenes resueltos de Matemáticas II Selectividad (EBAU) Cantabria
Exámenes resueltos de Matemáticas II Selectividad (EvAU) Castilla-La Mancha
Exámenes resueltos de Matemáticas II Selectividad (EBAU) Canarias
Exámenes resueltos de Matemáticas II Selectividad (EAU) País Vasco