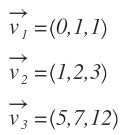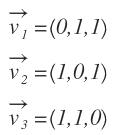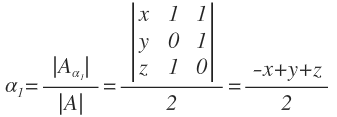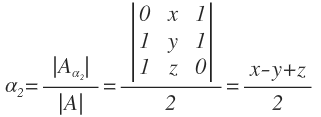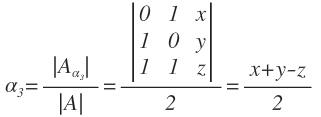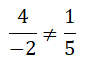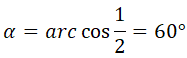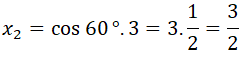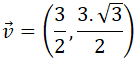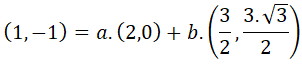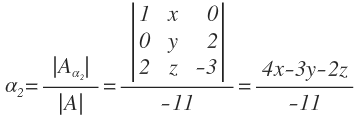A continuación te voy a explicar qué es un sistema generador de vectores y una base vectorial. Veremos también un concepto fundamental como son los vectores linealmente independientes. Todo ello con ejemplos y ejercicios resueltos paso a paso.
Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Vectores linealmente independientes
Decimos que n vectores son linealmente independientes si cuando al multiplicarlos por un coeficiente, su suma es igual a cero:
Por tanto, cuando los vectores son linealmente independientes, para que se cumpla la condición anterior, todos los coeficientes deben ser iguales a cero:
Si alguno de esos coeficientes es distinto de cero, los vectores serán linealmente dependientes:
Si los vectores son linealmente dependientes significa que algún vector se puede expresar como combinación lineal de otros vectores que forman el sistema.
Ejemplo de vectores linealmente independientes
Vamos a comprobar si los siguientes vectores son linealmente independientes o no:
En primer lugar, aplicamos la condición de multiplicar cada vector por un coeficiente, sumarlos e igualar la suma a cero:
Sustituimos cada vector por sus coordenadas, así como el 0, que lo ponemos también en forma de vector:
Ahora multiplicamos cada coeficiente por las coordenadas del vector:
En el primer miembro, sumamos cada una de las coordenadas y las expresamos en un solo vector:
Finalmente igualamos cada coordenada del primer miembro, con la misma coordenada del segundo miembro, que en este caso es igual a cero:
Nos queda un sistema de tres ecuaciones lineales con tres incógnitas que debemos resolver, cuyas incógnitas son los coeficientes que multiplican a los vectores.
Para que los vectores sean linealmente independientes, el sistema debe tener una única solución, es decir, debe ser un sistema compatible determinado, con los coeficientes igual a cero como solución.
En este caso, la matriz de los coeficientes queda:
Cuyo determinante es igual a cero:
Al ser el determinante igual a cero, el rango es menor que 3. En este caso, tanto el rango de la matriz de los coeficientes como el rango de la matriz ampliada es igual a 2, lo que significa que el sistema es compatible indeterminado:
Un sistema compatible indeterminado tiene infinitas soluciones, luego no tiene una única solución como estamos buscando, lo que significa que los vectores son linealmente dependientes.
Sistema de generadores
Diremos que un conjunto de vectores es un sistema generador del espacio vectorial V, si se puede expresar cualquier vector como la suma del producto de un coeficiente por cada uno de los vectores que forman el sistema de generadores, es decir:
Los coeficientes α1, α2, α3, …, αn son las coordenadas del vector V respecto del sistema de generadores
Ejemplo de sistema de generadores
Tenemos el siguiente conjunto de vectores, los cuales forman un sistema de generadores:
Por tanto, podemos expresar cualquier vector como combinación lineal de esos vectores. Vamos a obtener las coordenadas de un vector genérico respecto del sistema generadores, cuyas coordenadas iniciales son x, y y z:
Tenemos que expresar este vector como combinación lineal de los vectores del sistema de generadores:
En primer lugar sustituimos cada vector por sus coordenadas:
Multiplicamos los vectores del segundo miembro por sus coeficientes:
Sumamos cada una de las coordenadas y las expresamos en un solo vector:
Igualamos cada coordenada del primer miembro con la misma coordenada del segundo miembro, quedándonos el siguiente sistema de ecuaciones, que debemos resolver y hallar el valor de los coeficientes α1, α2 y α3 en función de x, y y z:
La matriz de los coeficientes es:
Cuyo determinante es igual a 2:
El determinante de la matriz de los coeficientes es distinto de cero, luego su rango es igual a 3, igual al rango de la matriz ampliada, por lo que el sistema es compatible determinado:
Al ser el sistema compatible determinado, el sistema tiene solución y pasamos a resolverlo mediante la regla de Cramer y nos queda:
Por tanto, para expresar cualquier vector respecto de este sistema de generadores, tan solo tenemos que sustituir x, y y z por las coordenadas del vector en estas expresiones, que es lo mismo que repetir todo el proceso con unas coordenadas concretas del vector v.
Base vectorial
Vamos a ver primero en qué es una base vectorial en R2.
Dos vectores forman una base vectorial, si se puede expresar cualquier vector como combinación lineal de esos dos vectores.
Si los vectores v1 y v2 forman una base vectorial se designa de la siguiente manera:
Y cualquier vector v puede expresarse como combinación lineal de los vectores v1 y v2:
donde los coeficientes a y b son las coordenadas del vector v con respecto a la base B:
Vamos a verlo gráficamente para que se entienda mejor.
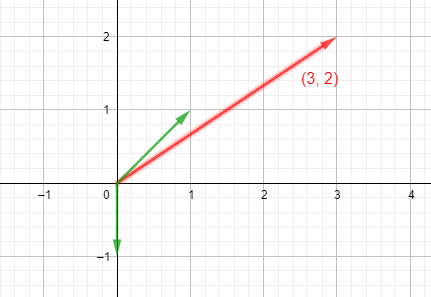
Tenemos el siguiente vector:
Para representarlo en los ejes de coordenadas, fijamos el extremo en el (0,0) y su extremo lo representamos avanzando 3 unidades a la derecha y 2 hacia arriba. Nos queda:
Hasta aquí todo es como siempre, ¿no?
Pues sin saberlo, estamos representando el vector con respecto a esta base:
llamada base canónica (la veremos más abajo con más detalle).
Si representamos los vectores de la base nos queda:
Lo que hacemos inconscientemente es una combinación lineal de los vectores de la base, ya que el vector (3,2) lo podemos formar como la suma de 3 vectores (1,0) más 2 vectores (0,1):
Es decir, el vector (3,2) lo podemos expresar como una combinación lineal de los vectores de la base canónica:
donde los coeficientes 3 y 2 son la coordenada x y la coordenada «y» del vector en la base canónica, que es en la base que están todos los vectores si no nos dicen nada.
Cualquier vector podrías expresarlo como combinación lineal de los vectores de la base canónica, siguiendo el mismo razonamiento.
Ahora bien, el mismo vector puede representarse con respecto a las coordenadas de otra base distinta.
Por ejemplo, supongamos que tenemos la siguiente base:
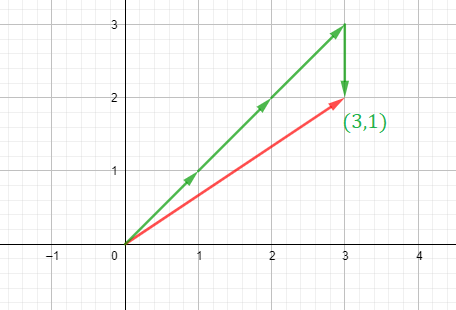
Si representamos los vectores de la base nos queda:
El mismo vector lo podemos formar como una combinación de los vectores de la base B’, ya que es igual a 3 veces el vector (1,1) más 1 vez el vector (0,-1):
En este caso, las coordenadas del vector con respecto a la base B’ son (3,1), que son las veces que se repiten los vectores de la nueva base para formar el vector:
Date cuenta de que el vector es el mismo, solo que con otra referencia distinta. Puedes considerarlo como si tuvieras unos nuevos ejes de coordenadas.
Vamos a ver ahora qué es una base vectorial en R3:
Una base vectorial es un sistema de generadores cuyos vectores son linealmente independientes. Por tanto, cualquier vector se puede expresar respecto a una base como combinación lineal de sus vectores:
Los coeficientes α1, α2, α3, …, αn son las coordenadas del vector V respecto de la base.
Ejemplo de base vectorial en R3
Vamos a comprobar si el conjunto de vectores del sistema de generadores anterior forman una base:
Para ello, debemos comprobar si esos vectores son linealmente independientes, que lo hacemos igualando a cero la suma de las coordenadas α1, α2 y α3 por cada uno de los vectores:
De donde obtendremos el siguiente sistema de ecuaciones:
Que podemos resolverlo tal y como hemos hecho anteriormente. Yo directamente voy a sustituir x, y y z por cero en las expresiones anteriores para α1, α2 y α3 y nos queda:
Todas las coordenadas son iguales a cero, por lo que los vectores son linealmente independientes y por tanto el sistema de generadores es una base:
Cómo calcular las coordenadas de un vector respecto de una base en R2
Vamos a ver ahora el caso de que tengamos las coordenadas de un vector con respecto a una base y nos piden las coordenadas de ese mismo vector con respecto a otra base.
Por ejemplo, tenemos el siguiente vector con respecto a la base canónica (si no nos dicen nada, siempre está en esta base):
y nos piden hallar las coordenadas del vector en la base B:
Sabemos que si tenemos una base cualquiera:
Cualquier vector v puede expresarse como combinación lineal de los vectores v1 y v2:
donde los coeficientes a y b son las coordenadas del vector v con respecto a la base B:
Por tanto, el vector (2,-5) lo tenemos que expresar como combinación lineal de los vectores de la base B, es decir, sustituimos v por (2,-5), y v1 y v2 por las coordenadas de los vectores de la base tenemos que calcular los coeficientes a y b:
Operamos en el segundo miembro, multiplicando los coeficientes por los vectores:
Y operamos en cada coordenada por separado:
Finalmente, igualamos las coordenadas de ambos miembros, quedándonos un sistema de dos ecuaciones con dos incógnitas:
Cuyas soluciones son:
Por lo que las coordenadas del vector (2,-5) con respecto de la base B son:
Condiciones para que dos vectores sean una base vectorial
Dos vectores pueden formar una base vectorial siempre y cuando estos dos vectores tengan distinta dirección, es decir, siempre y cuando los vectores no sean paralelos.
Así que, para determinar si dos vectores forman una base vectorial, lo único que tenemos que hacer es demostrar que esos dos vectores no son paralelos.
Dos vectores son paralelos entre sí cuando sus coordenadas son proporcionales.
Por ejemplo, los vectores a y b son paralelos:
ya que las coordenadas del vector «a» son iguales a las del vector b multiplicadas por 2.
es decir, tienen la misma proporción entre sus coordenadas:
Así que, el resultado de dividir las coordenadas x de ambos vectores es igual al resultado de dividir las coordenadas «y» de ambos vectores:
Al ser los vectores a y b paralelos no pueden formar una base vectorial.
Vamos a ver otro ejemplo
¿Los siguientes vectores pueden ser una base vectorial?
Para ver si los vectores pueden forman una base vectorial, tenemos que comprobar si son paralelos y para demostrar que dos vectores no son paralelos, tenemos que comprobar que tengan una proporción distinta entre sus coordenadas.
La proporción entre las coordenadas x es distinta a la proporción entre las coordenadas «y»:
por tanto, los vectores no son paralelos y sí pueden formar una base vectorial.
Cómo hallar las coordenadas de un vector respecto a una base en R3
Vamos a ver cómo ahora cómo calcular las coordenadas de un vector con respecto a una base en R3:
Vamos a calcular las coordenadas del vector U=(1,2,3) respecto de la siguiente base:
Vamos a expresar las coordenadas del vector u como combinación lineal de los vectores de la base:
En este caso, lo que nos están preguntando son las coordenadas α1, α2 y α3:
Empezamos sustituyendo las coordenadas de cada vector en la expresión:
Multiplicamos cada vector por su coeficiente:
Sumamos cada una de las coordenadas y las expresamos en un solo vector:
Nos queda el siguiente sistema de ecuaciones:
Para hallar la solución de las coordenadas, debemos resolver el sistema, comprobando previamente que se trata de un sistema compatible determinado.
Como ya lo tenemos resuelto de antes, con el vector (x,y,z), tan sólo tenemos que sustituir x, y y z por las coordenadas de nuestro vector:
Por lo que esas son las coordenadas del vector u con respecto de la base:
Tipos de bases vectoriales
Base ortogonal
Una base es ortogonal cuando los vectores que la forman son perpendiculares (u ortogonales) entre ellos.
Dos vectores son perpendiculares cuando su producto escalar es igual a 0:
Base ortonormal
Si los vectores que forman la base, además de ser perpendiculares entre ellos, son vectores unitarios, es decir, que su módulo es igual a 1, la base es ortonormal:
Base canónica
La base canónica es una base ortonormal formada por los siguientes vectores, uno en dirección del eje x y otro en dirección del eje y:
Cualquier vector perteneciente al plano puede expresarse como combinación lineal de los vectores de la base canónica
Por ejemplo:
En R³, la base canónica está formada por los siguientes vectores, uno en dirección del eje x y otro en dirección del eje y:
Cualquier vector perteneciente a R³ puede expresarse como composición lineal de los vectores de la base canónica:
Ejercicios resueltos sobre base de un espacio vectorial
Ejercicio 1
Expresa las coordenadas del siguiente vector:
con respecto a las siguientes bases:
El vector v puede expresarse como combinación lineal de los vectores de la base:
donde v1 y v2 son los vectores de la base y a y b son las coordenadas del vector v con respecto a la base.
Sustituimos v, v1 y v2 por sus valores, donde v1 y v2 son las coordenadas de los vectores de la base B:
Multiplicamos los coeficientes por los vectores en el segundo miembro:
Operamos en cada coordenada:
E igualamos las coordenadas de cada miembro, dando lugar al siguiente sistema de ecuaciones:
cuyas soluciones son:
Por los que las coordenadas de v con respecto de la base B son:
Si lo representamos gráficamente queda de la siguiente forma:
Ahora vamos a calcular las coordenadas del vector v con respecto a la base B’.
En la fórmula:
sustituimos v, v1 y v2 por sus valores, donde ahora v1 y v2 son las coordenadas de los vectores de la base B’:
Multiplicamos a y b por sus vectores:
Operamos en cada coordenada:
E igualamos coordenadas de ambos miembros.
El sistema de ecuaciones que nos queda es el siguiente:
Y sus soluciones son:
Por tanto, las coordenadas de v con respecto de la base B’ son:
Gráficamente nos queda:
Ejercicio 2
Tenemos el vector u:
Obtener un vector v, para que la base B cumpla las siguientes condiciones:
a) Sea una base
b) Sea una base ortogonal
c) No sea una base
d) Sea una base ortonormal
Apartado a:
Para que dos vectores formen una base, el único requisito es que los vectores no sean paralelos, por lo tanto, me sirve cualquier vector que no sea proporcional al vector u, como por ejemplo este escogido al azar:
Compruebo que no es paralelo al vector u:
No son paralelos, por lo que la base queda:
Apartado b:
Para que la base sea ortogonal, los vectores que la forman tienen que ser perpendiculares u ortogonales y para que eso ocurra, su producto escalar tiene que ser igual a cero:
No conocemos las coordenadas del vector v que cumple esa condición, así que les llamamos x e y:
Realizamos su producto escalar:
Operamos y me queda una ecuación con dos incógnitas:
Como no tengo otra ecuación para formar un sistema de dos ecuaciones y resolverlo, vamos a suponer un valor para x y calcularemos su correspondiente valor de «y».
Suponemos que x=1, así que en la ecuación, sustituimos la x por 1 y despejamos la «y»:
Por tanto, las coordenadas de v son:
Y la base en este caso es:
Puedes darle a x cualquier valor (menos x=0) y obtener su correspondiente valor de y, por lo que se podrían obtener infinitos vectores v perpendiculares a u. No puedes darle a x el valor 0, ya que el valor de «y» también saldría 0 y (0,0) no es ningún vector.
Apartado c:
Para que u y v no sean una base, ambos vectores deben ser paralelos. Para que el vector v sea paralelo a u, basta on multiplicarlo por cualquier número.
Yo voy a multiplicarlo por ejemplo por 3:
Este vector v es paralelo a u y por tanto no pueden formar una base.
Apartado d:
Para que una base sea ortonormal, sus vectores deben ser perpendiculares y su módulo debe ser igual a 1.
Vamos a calcular el módulo del vector u:
Este vector ya pertenece a la base y no es igual a 1:
Por lo que no es posible que u y v formen una base ortonormal, sean cuales sean las coordenadas de v.
Ejercicio 3
Sea B una base formada por los vectores u y v:
de los cuales se sabe que el módulo del vector u es igual a 2:
el módulo del vector v es igual a 3:
y el producto escalar de u por v es igual a 3:
Por otro lado, sea B’ una base ortonormal:
Y sean los vectores x e y:
Calcular:
a) El producto escalar de x por y en la base B:
a) El producto escalar de x por y en la base B’:
Apartado a:
Empezamos obteniendo las coordenadas de los vectores u y v que forman la base B, a partir de su producto escalar.
La fórmula del producto escalar es:
Sustituimos los datos que sabemos:
Despejamos el coseno del ángulo:
Y finalmente obtenemos el ángulo haciendo la inversa del coseno:
Por otro lado, suponemos que el vector u está en el eje x y como tiene módulo 2, sus coordenadas son:
Las coordenadas de v las expresamos con incógnitas ya que las desconocemos por el momento:
Gracias al producto escalar, sabemos que el ángulo entre los dos vectores es de 60º y como el vector u está en la horizontal, el vector v forma un ángulo de 60º con respecto a la horizontal:
Así que para obtener sus coordenadas, vamos a descomponerlo.
Con la fórmula del seno de 60º, obtenemos su coordenada y:
Con la fórmula del coseno de 60º, obtenemos su coordenada x:
Por tanto, las coordenadas del vector v son:
Y la base B estará formado por los vectores:
Una vez conocemos las coordenadas de los vectores de la base B, vamos a expresar las coordenadas de los vectores x e y con respecto a la base B.
Empezamos con el vector x:
El vector x puede expresarse como combinación lineal de u y v:
Sustituimos los vectores por sus coordenadas:
Multiplicamos los coeficientes por los vectores en el segundo miembro:
Operamos en cada coordenada:
E igualamos las coordenadas de cada miembro, dando lugar al siguiente sistema de ecuaciones:
cuyas soluciones son:
Así que, las coordenadas de v con respecto de la base B son:
Hacemos lo mismo con el vector «y»:
El vector «y» puede expresarse como combinación lineal de u y v:
Sustituimos los vectores por sus coordenadas:
Multiplicamos los coeficientes por los vectores en el segundo miembro:
Operamos en cada coordenada:
E igualamos las coordenadas de cada miembro, dando lugar al siguiente sistema de ecuaciones:
cuyas soluciones son:
Las coordenadas de y con respecto de la base B son:
Una vez tenemos expresadas las coordenadas de los vectores x e y con respecto de la base B, ya podemos calcular su producto escalar en dicha base, con la expresión analítica del producto escalar:
Apartado b:
La base B’ ortonormal:
está formada por los siguientes vectores:
que corresponden a los vectores de la base canónica.
Los vectores x e y ya están referidos a la base B’, por lo que sus coordenadas son las que nos dice el enunciado:
Por tanto, el producto escalar de x e y en la base B’ es:
Ejercicio 4
Comprueba que los siguientes vectores son una base:
Calcula las coordenadas de los siguientes vectores respecto de la base anterior:
En primer lugar, vamos a expresar un vector genérico de coordenadas (x,y,z) con respecto de la base:
Este vector se puede expresar como combinación lineal de los vectores de la base:
Sustituimos cada vector por sus coordenadas:
Multiplicamos los vectores por los coeficientes:
Y sumamos cada una de las coordenadas expresándolas en un solo vector:
De esta expresión obtengo un sistema de ecuaciones, de donde hay que resolver los coeficientes α1, α2 y α3 en función de x, y y z:
La matriz de los coeficientes es:
Cuyo determinante es igual a -11:
El determinante de la matriz de los coeficientes es distinto de cero, luego su rango es igual a 3, igual al rango de la matriz ampliada, por lo que el sistema es compatible determinado:
Lo resolvemos por la regla de Cramer y queda:
Ya tenemos expresado un vector cualquiera con respecto a la base dada. Ahora, para determinar las coordenadas de cualquier vector, tan sólo tenemos que sustituir x, y y z por las coordenadas del vector en cuestión.
Vamos a comprobar si realmente se trata de una base. Para ello, los vectores deben ser linealmente independientes, por lo que la combinación lineal de los vectores debe ser igual a cero:
Sustituimos los vectores por sus coordenadas:
De donde obtenemos el siguiente sistema de ecuaciones:
Es el mismo sistema que teníamos antes, solo que igualado a cero. Por tanto, para resolverlo, sustituyo x, y y z por 0 y opero:
La solución de los 3 coeficientes es igual a cero, luego los vectores son linealmente independientes:
Al ser los vectores linealmente independientes, efectivamente, el sistema de generadores se trata de una base.
Vamos a expresar el vector x con respecto a la base:
Se tiene que cumplir:
Sustituimos los vectores por sus coordenadas:
Nos queda el siguiente sistema de ecuaciones:
Para resolverlo, sustituyo x, y y z por 1 y opero:
Las coordenadas del vector x con respecto de la base son:
Por último hacemos lo mismo con el vector y:
La combinación lineal de los vectores de la base debe ser igual a este vector:
Sustituimos los vectores por sus coordenadas:
Nos queda el siguiente sistema de ecuaciones:
Para resolverlo, sustituyo x, y y z por 1, 2 y 3 respectivamente y opero:
Las coordenadas del vector y con respecto de la base son:
¿Necesitas ayuda en matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más:
Exámenes resueltos de Matemáticas II Selectividad (EvAU) Navarra
Exámenes resueltos de Matemáticas II Selectividad (PAU) Valencia
Exámenes resueltos de Matemáticas II Selectividad (PevAU) Andalucía
Exámenes resueltos de Matemáticas II Selectividad (EBAU) Cantabria
Exámenes resueltos de Matemáticas II Selectividad (EvAU) Castilla-La Mancha
Exámenes resueltos de Matemáticas II Selectividad (EBAU) Asturias
Exámenes resueltos de Matemáticas II Selectividad (ABAU) Galicia