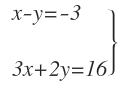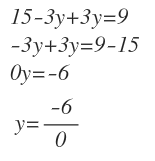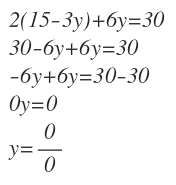En esta lección te voy a explicar los tipos de sistemas de ecuaciones que existen, dependiendo del número de soluciones, con un ejemplo de cada uno de los tipos de sistemas.
Los sistemas de dos ecuaciones con dos incógnitas, en general tienen una única solución, pero no siempre ocurre así. Puede ser que el sistema de dos ecuaciones no tenga solución y que otras tenga infinitas soluciones.
¿Por qué ocurre ésto? Vamos a verlo más despacio
Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Solución de un sistema de dos ecuaciones
En un sistema de dos ecuaciones con dos incógnitas como por ejemplo éste:
Cada ecuación corresponde a una recta.
Cuando resuelves un sistema de dos ecuaciones con dos incógnitas, lo que realmente estás haciendo es encontrando el punto de corte de las dos rectas, si lo tuviera, porque a vece no se cortan (más abajo veremos que a veces no se cortan)
La ecuación de una recta tiene esta forma:
Podemos poner cada de las ecuaciones del sistema de esa forma para que quede más claro que se trata de dos rectas:
Primera ecuación:
Segunda ecuación:
Pues bien, en función de la posición de las dos rectas, o dicho de otra forma, del número de soluciones de los sistemas de dos ecuaciones podemos hablar de sistemas compatibles determinados, sistemas compatibles indeterminados y sistemas incompatibles, que paso a explicarte con más detalle a continuación.
[et_bloom_inline optin_id=»optin_35″]
Sistema compatible determinado
Un sistemas compatible determinado es el sistema de dos ecuaciones que al resolverlos tiene una solución, es decir, pueden resolverse.
La solución es el punto donde se cortan las dos rectas si las representas gráficamente. Por tanto, las dos rectas del sistema se cortan en un punto.
Vamos a verlo con un ejemplo. Tenemos este sistema de dos ecuaciones:
Vamos a resolverlo por el método de sustitución. De la primera ecuación despejo la x:
Este valor de x, lo sustituyo en la segunda ecuación:
Opero y despejo “y”:
Ahora este valor de y, lo sustituyo en la ecuación donde despejé la x:
Y obtengo el valor de x:
Por lo que la solución del sistema de dos ecuaciones es:
O lo que es lo mismo, si representas las dos rectas, su punto de corte es (2,5).
Vamos a representar las dos rectas y verás que el punto donde se cortan es la solución que acabamos de calcular:
Sistema incompatible
Como te comenté al principio, no siempre los sistemas de dos ecuaciones tienen solución.
Puede que las rectas sean paralelas y nunca lleguen a cortarse. En este caso estamos hablando de un sistema incompatible.
Vamos a verlo con un ejemplo:
Si representas las dos rectas de este sistema verás que son paralelas y nunca se corta, por tanto, es un sistema incompatible:
Las rectas son paralelas cuando tienen la misma pendiente, pero distinta ordenada, es decir, en la fórmula:
m es la pendiente
n es la ordenada
Si en el sistema anterior, ponemos las dos rectas de esta forma:
Vemos que tienen la misma pendiente, es decir, el número que está delante de la x es igual, pero la ordenada cambia (n es distinto)
¿Cómo saber si un sistema es incompatible sin necesidad de representar las rectas gráficamente?
Vamos a resolver un sistema de dos ecuaciones para verlo:
Sin saber que es un sistema incompatible, empezamos a resolverlo. Despejamos la x en la primera ecuación:
Y este valor de x lo sustituyo en la segunda ecuación:
Opero y despejo la y:
Me queda un número dividido entre cero. Un número no se puede dividir entre cero, por lo tanto el sistema no tiene solución.
Cuando al resolver una de las incógnitas, me queda un número dividido entre cero, el sistema no tiene solución y por tanto es un sistema incompatible.
Sistema compatible indeterminado
Las dos rectas pueden estar de una tercera forma, además de cortarse en un punto o de ser paralelas. Pueden ser coincidentes, es decir, que una recta esté encima de la otra.
Cuando una recta está encima de otra, en realidad son la misma recta.
En este caso, el sistema tiene infinitas soluciones, porque recuerda que cuando resolvemos un sistema estamos buscando el punto de corte y en este caso todos sus puntos son comunes.
Para entender esto, tienes que entender el concepto de ecuación equivalente.
Puedes multiplicar o dividir todos los términos de una ecuación por el mismo número y la ecuación resultante sería equivalente a la original. Si la representaras sería la misma recta.
Por ejemplo, esta ecuación:
Puedo multiplicar todos sus términos por 2 y la ecuación resultante sería:
Y por tanto sería una ecuación equivalente a la original.
Bien, en los sistemas compatibles indeterminados, realmente tenemos dos ecuaciones equivalentes, que equivaldría a tener dos ecuaciones iguales.
Por ejemplo, este sistema de dos ecuaciones:
Tiene dos ecuaciones equivalentes. Acabamos de ver que la segunda ecuación es igual a la primera multiplicada por 2.
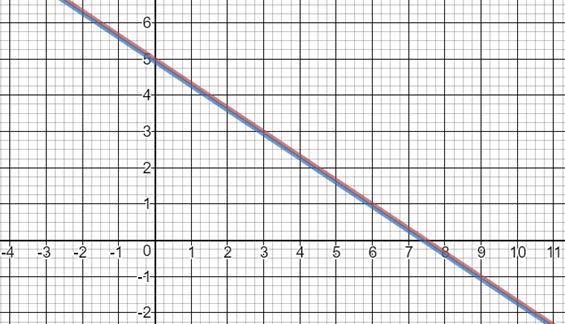
Si representamos cada recta nos queda:
Es lo mismo que si resolviéramos un sistema con las dos ecuaciones iguales:
¿Cómo saber si un sistema es compatible indeterminado sin tener que representarlo? Vamos a resolver uno para que lo veas:
De la primera ecuación despejo la x:
Sustituyo este valor de x en la segunda ecuación:
Opero y despejo la y:
Me queda cero dividido entre cero. Cero entre cero es un número indeterminado, por lo que la «y» puede tomar cualquier valor y por tanto, el sistema tiene infinitas soluciones.
Cuando al resolver una de las incógnitas, me queda cero dividido entre cero, el sistema tiene infinitas soluciones y por tanto es un sistema compatible indeterminado.
Discusión de sistemas de dos ecuaciones con dos incógnitas
Discutir un sistema significa estudiar las posibles soluciones del sistema en función de un parámetro que no conocemos del sistema de ecuaciones de dos incógnitas y definir de qué tipo de sistema se trata en cada caso.
Por ejemplo, en el siguiente sistema, el coeficiente de la x de la primera ecuación es el parámetro «a»:
Vamos a discutir el sistema calculando las en función de los valores del parámetro «a».
Empezamos resolviendo el sistema, cuya solución se quedará en función de «a».
De la primera ecuación:
Despejamos «y»:
En la segunda ecuación:
Sustituimos la «y» por la expresión que acabamos de obtener:
Operamos para eliminar el paréntesis:
Dejamos los términos con x en el primer miembro y los términos sin x en el segundo miembro:
Ya que en el primer miembro, uno de los coeficientes está en función de «a», no podemos operar con ellos directamente, por lo que sacamos factor común a la x para poder despejarla:
Y pasamos el contenido del paréntesis al segundo miembro dividiendo:
Llegados a este punto, el denominador de la fracción que me ha quedado va a ser el que marque el número de soluciones del sistema y por tanto el tipo de sistema.
Si el denominador es igual a cero, entonces el número quedará dividido entre cero:
De la ecuación que resulta de igualar el denominador a cero, podemos despejar la «a»:
Por tanto, siempre que a sea 1/3, es decir, que el denominador sea cero, me quedará un número entre cero y el sistema es un sistema incompatible:
Al ser un sistema incompatible, no tiene ninguna solución.
Por otro lado, siempre que a no sea igual a 1/3, entonces el denominador nunca será cero y por tanto estaremos dividiendo entre un número y el sistema tendrá una única solución, por lo que será un sistema compatible determinado:
¿Necesitas ayuda con las matemáticas? ¿Quieres que te explique cualquier duda que te surja paso a paso?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: