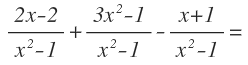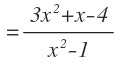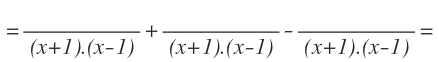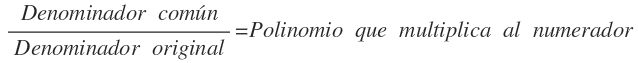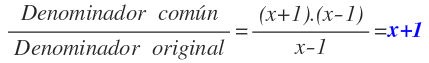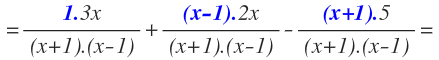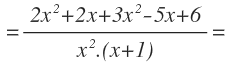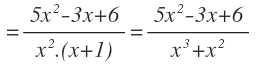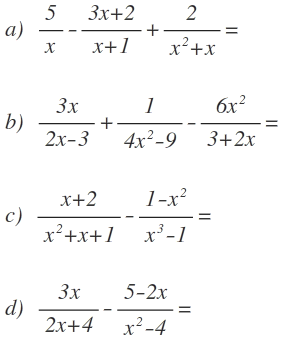A continuación te voy a enseñar cómo sumar y restar fracciones algebraicas tanto con el mismo denominador, como con distinto denominador.
Si has llegado hasta aquí es porque quieres aprender a resolver algún ejercicio. ¿Has pensado en apuntarte a clases de matemáticas online?. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
El procedimiento es el mismo que para sumar o restar fracciones numéricas, es decir, necesitamos tener el mismo denominador para sumar y restar fracciones y cuando no lo tenemos, tenemos que reducir las fracciones a denominador común, con la diferencia de que con las fracciones algebraicas, en vez de números, trabajamos con polinomios.
Vamos a verlo paso a paso.
Suma y resta de fracciones algebraicas con igual denominador
Empezamos con la suma y resta de fracciones algebraicas que tienen el mismo denominador, como por ejemplo ésta:
En este caso, se mantiene el denominador y se opera con los numeradores. Podemos dejar una sola fracción con el denominador común y con los términos de ambos numeradores:
Y después agrupar términos semejantes en el numerador:
Sumar y restar fracciones algebraicas que tienen el mismo denominador es así de sencillo. Sin embargo, hay que tener mucho cuidado en la resta de fracciones algebraicas, ya que el signo menos, afecta a todos los términos del numerador de la fracción que tenga detrás.
Vamos a ver un ejemplo con resta de fracciones algebraicas para que lo entiendas mejor:
Tenemos el mismo denominador y por tanto, podemos unir todos los numeradores en uno sólo. Pero ahora, delante de la última fracción tenemos un signo menos y como te comentaba antes, afecta a los dos términos del numerador de la fracción que tiene detrás. Por tanto, para que siga siendo así, los términos afectados por el signo menos deben ir encerrados entre paréntesis:
En el siguiente paso, eliminamos el paréntesis, cambiando de signo a los términos que tiene dentro:
Y por último, agrupamos términos semejantes en el numerador:
Un error muy común es no encerrar entre paréntesis los términos del numerador de la fracción que está precedida por un signo menos. En caso de no hacerlo, solamente le cambiamos el signo al primer término, lo cual es un error:
Suma y resta de fracciones algebraicas con distinto denominador
Ahora te voy a explicar cómo sumar y restar fracciones algebraicas con diferente denominador.
Ten en cuenta que sólo se pueden sumar o restar fracciones algebraicas que tengan el mismo denominador, por lo que si tienen distinto denominador, antes hay que reducirlas a común denominador, tal y para sumar y restar fracciones numéricas con distinto denominador.
Obtenemos el denominador común calculando el mínimo común múltiplo de los denominadores.
Por ejemplo, tenemos sumas y restas de fracciones algebraicas, cuyos denominadores no son iguales:
El primer paso será reducirlas a denominador común calculando el mínimo común múltiplo de los denominadores:
Para ello, previamente, hay que descomponer los polinomios. Los polinomios de la segunda y la tercera fracción algebraica no se pueden descomponer por ser de grado 1. Descomponemos el denominador de la primera fracción y nos queda:
Por tanto, tenemos los factores (x+1) y (x-1), sin ningún exponente (o elevados a 1), por lo que el mínimo común múltiplo será la multiplicación de ambos:
Vamos a transformar cada fracción algebraica que ya teníamos en una fracción algebraica equivalente con el denominador común que acabamos de calcular.
Colocamos nuestro nuevo denominador en cada una de las fracciones, listo para empezar a calcular el nuevo numerador de cada fracción:
Para transformar una fracción algebraica en otra que sea equivalente, tenemos que multiplicar el numerador y el denominador por el mismo polinomio.
Al colocar el denominador común directamente, ya hemos multiplicando el denominador original por un polinomio, por lo que falta multiplicar el numerador por el mismo polinomio para que la fracción algebraica sea equivalente.
¿Cómo obtenemos ese polinomio por el que hay que multiplicar cada numerador?
Se obtiene dividiendo el denominador común entre el denominador original de cada fracción algebraica:
Vamos a verlo con la primera fracción algebraica de la operación del ejemplo:
Inicialmente teníamos en el denominador el polinomio (x²-1) y en la nueva fracción equivalente tenemos como denominador (x+1).(x-1):
En este caso, el denominador común y el denominador original coinciden ya que (x²-1)=(x+1).(x-1), por tanto, al tener el mismo denominador, el numerador lo multiplicamos por 1, o en otras palabras, se queda igual:
Si calculamos el polinomio por el que multiplicar el numerador mediante la fórmula anterior, obtenemos ese 1:
Vamos a ver cuál es el polinomio por el que tenemos que multiplicar la segunda fracción:
Teníamos como denominador original (x+1) y ahora tenemos (x+1).(x-1) que es el denominador común. Al dividir el denominador común entre el denominador original nos queda (x-1):
Que es el polinomio por le que tenemos que multiplicar el numerador para que la fracción algebraica sea equivalente a la original:
Y por último, hacemos lo mismo con la tercera fracción algebraica:
Dividimos el denominador común entre el denominador original:
Y el resultado lo multiplicamos por el numerador:
De esta forma hemos obtenido las tres fracciones algebraicas equivalentes con el denominador común:
Ya tienen el mismo denominador y por tanto, ya se pueden sumar y restar, pero antes, multiplicamos en los numeradores:
Ahora ya podemos unir todos los numeradores en una sola fracción con el denominador común. Ten en cuenta, como siempre, que el signo menor afecta a todos los términos del numerador que tiene detrás y por eso, debemos encerrar esos términos entre paréntesis (no me cansaré de repetirlo):
Eliminamos el paréntesis del numerador:
Agrupamos términos en el numerador y en el último paso, multiplicamos en el denominador para obtener el resultado final:
Vamos a resolver otro ejemplo paso a paso para que quede todavía más claro:
Tenemos una suma y resta de fracciones algebraicas con diferente denominador, por lo que tenemos que reducirlas a denominador común. Para ello obtenemos el mínimo común múltiplo de los denominadores:
Los denominadores de la primera y segunda fracción algebraica no se pueden descomponer. Descomponemos el denominador de la tercera fracción algebraica:
Tenemos como factores x, x² y (x+1). De entre x y x² nos quedamos con x² por tener mayor exponente y nos quedamos también con (x+1), por lo que el mcm es:
Dejamos preparada cada fracción algebraica con el nuevo denominador:
Multiplicamos cada numerador cada numerador por el polinomio obtenido de dividir el denominador común entre el denominador original:
Unimos todos los numeradores en una sola fracción, teniendo muy en cuenta el signo menos:
Operamos en el numerador eliminando paréntesis:
Y finalmente agrupamos términos y operamos en el denominador para obtener el resultado final:
Ejercicios propuestos
Resuelve las siguientes sumas y restas de fracciones algebraicas:
¿Necesitas clases de matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: