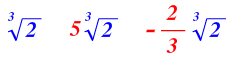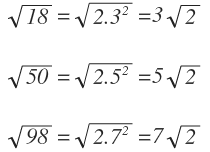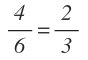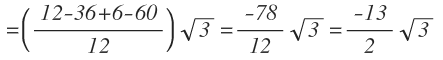A continuación voy a explicarte todo lo que necesitas saber para sumar y restar radicales (o raíces) paso a paso. Te indicaré las pequeñas dificultades que se te pueden presentar y cómo tienes que resolverlas.
Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Antes de aprender a sumar y restar radicales, es necesario que te enseñe un par de conceptos que vas a tener que aplicar.
En este vídeo tienes ejercicios resueltos paso a paso sobre cómo sumar y restar radicales:
Y si sigues leyendo, más abajo lo tienes todo explicado paso a paso:
Radicales semejantes
Los radicales semejantes son los que tienen el mismo índice y el mismo radicando, es decir, son los que son exactamente iguales.
Los radicales pueden ir multiplicados por un factor, llamado coeficiente, que puede ser distinto en los radicales semejantes.
Vamos a verlo con un ejemplo:
Estos tres radicales son semejantes, porque tienen el mismo índice y el mismo radicando. El coeficiente es distinto.
Sin embargo, este otro radical ya no sería semejante a los anteriores, porque tiene el mismo índice, pero el radicando es distinto:
No siempre los radicales semejantes se identifican directamente. A veces, es necesario simplificar el radical antes.
Por ejemplo, ¿estos radicales son semejantes?
A simple vista no, porque no tienen el mismo radicando.
Pero vamos a simplificar cada uno de los radicales, descomponiendo el radical para ponerlo en forma de potencia y después extrayendo factores fuera del radical, a ver qué pasa:
Al final, tienen el mismo índice y el mismo radicando, con un coeficiente distinto cada uno, por tanto sí que son semejantes.
Simplificación de radicales paso a paso
Los índices de los radicales y los exponentes de los radicandos se pueden multiplicar o dividir por el mismo número de la misma forma que se multiplica o divide por un número el numerador y el denominador de una fracción.
Como resultado, se obtendría un radical equivalente, es decir, su resultado sería el mismo
Igual que en una fracción se puede simplificar cuando se puede dividir el numerador y el denominador entre el mismo número y su resultado no varía:
De la misma forma, si el índice de la raíz y el exponente del radicando se pueden dividir entre el mismo número se pueden simplificar y el resultado sigue siendo el mismo:
Piensa que si pasamos estas raíces a su forma exponencial, lo que se hace es simplificar la fracción del exponente y como ya sabes, el valor de esa fracción no varía, por lo que el exponente sigue siendo el mismo.
Simplificar el índice y el exponente puede servirte para resolver raíces.
Por ejemplo, es complicado hallar la solución de la raíz cuarta de dos elevado a 8, pero al simplificar índice y exponente, el resultado es inmediato:
También es útil para hallar radicales semejantes.
En este ejemplo, los radicales no tienen ni el mismo índice ni el mismo exponente:
Pero si simplificas el índice y el exponente de la primera raíz, dividiéndolos entre 3, los radicales ya son semejantes
De la misma forma, puedes multiplicar el índice de la raíz y el exponente del radicando y obtendrás otra raíz equivalente.
Cómo sumar y restar radicales con distinto íncide
Antes de empezar a explicar la suma y resta de radicales hay que responder a una pregunta muy importante:
¿Cómo sumar y restar radicales con diferente índice?
Esta es una pregunta que se hacen muchos alumnos que pretenden realizar esta operacion, pero lo que desconocen es que no es posible sumar o restar radicales con índice diferente.
Ten en cuenta que sólo se pueden sumar y restar radicales semejantes.
Por tanto, no se pueden sumar y restar radicales con diferente índice. Sólo se pueden sumar y restar si tienen el mismo índice.
Dicho esto, vamos a ver cómo se suman y se restan los radicales semejantes.
Cómo sumar y restar radicales
Cuando se habla de sumar y restar radicales, realmente se trata de sumar o restar términos con raíces.
Para realizar sumar y restar radicales semejantes, lo que hacemos es mantener el radical semejante y sumar y restar los coeficientes (número que está multiplicando a la raíz).
Por ejemplo, vamos a sumar los tres radicales semejantes del apartado anterior:
En primer lugar comprobamos si los radicales son semejantes y vemos que sí, porque tienen todos el mismo índice y el mismo radicando. Aunque esta vez, ya sabíamos que eran semejantes.
Lo que se suma y resta son los coeficientes de cada uno de los términos y se mantiene el radical semejante:
Realizamos la suma y resta de los coeficientes y ya lo tenemos:
Se trata prácticamente de una suma y resta de números, que pueden ser números enteros o como en este caso, fracciones.
Sin embargo, como ya sabes, no siempre se sabe que los radicales son semejantes a simple vista. Lo más normal es que tengas que simplificarlos previamente para comprobar si son semejantes.
Vamos a ver un ejemplo:
En esta operación, parece que los radicales no son semejantes y que no se puede sumar y restar los radicales. Pero para comprobar que realmente es así, vamos a empezar descomponiendo los radicandos en factores:
Una vez que tenemos los radicandos descompuestos y en forma de potencia, extraemos factores:
Si quieres aprender a extraer factores paso a paso, lo tienes explicado en la cuarta lección del Curso de Raíces, disponible sólo para los alumnos premium.
Ahora que hemos extraído factores, podemos comprobar que efectivamente los radicales sí que son semejantes, ya que todos son raíz de 2.
Date cuenta también, que los factores que hemos extraído, se quedan multiplicando también al coeficiente que el radical ya tenía delante.
El siguiente paso es multiplicar los números que tenemos delante de cada raíz, quedando:
Y finalmente, sumamos y restamos los coeficientes, manteniendo un único radical:
Puede darse el caso de que no te quede un único radical semejante. Lo que tienes que hacer en ese caso es sumar los que sean semejantes y los que no, dejarlos tal y como están. Vamos a verlo con otro ejemplo:
Igual que en el ejemplo anterior, tenemos que simplificar los radicales para comprobar si son semejantes. Descomponemos los radicandos y los escribimos en forma de potencia:
Y extraemos factores:
Podemos ver que dos de los radicales que tienen 3 como radicando son semejantes, pero el que tiene 2 como radicando no es semejante.
Multiplicamos los factores que tenemos delante de los radicales:
Y sumamos sólo los radicales que son semejantes, los que tienen 3 de radicando. Con el otro radical no podemos hacer nada por lo que la solución se queda con los dos radicandos:
Por último, vamos a ver otro caso de los que te puedas encontrar y es que los radicandos estén en forma de fracción. Por ejemplo:
Para empezar, debes aplicar la propiedad de que la raíz de una fracción es igual a una fracción de raíces y se indica el numerador y el denominador en forma de raíz:
También tienes una lección dedicada a las propiedades de las raíces en el Curso de Raíces.
Descomponemos todos los radicandos y los escribimos en forma de potencia, tanto los del numerador como los del denominador:
Extraemos factores de todos los radicales. Los factores que extraigas del numerador, se quedan en el numerador y los que extraigas del denominador, se quedan en el denominador:
Ahora operamos con los números que tenemos delante de los radicales. En un primer paso, los voy a dejar delante de cada radical en forma de fracción, para que veas que vuelves a tener radicales semejantes multiplicados por un coeficiente (que en este caso es una fracción), como en los ejemplos anteriores:
Sumamos y restamos los coeficientes:
En vez de dejar en forma de fracción los números delante de cada radical, puedes también aprovechar para operar en algunos términos, como por ejemplo en el primer término, 2/2 = 1 y en el último término 15/3 = 5. No es necesario ir arrastrando los números hasta el último paso para operar.
Como ves, para saber sumar y restar radicales, a parte de lo que te explico aquí es necesario que domines otros conceptos como la descomposición factorial, simplificación de fracciones o las propiedades de las potencias.
¿Necesitas ayuda con las matemáticas? ¿Quieres que te explique cualquier duda que te surja paso a paso?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: