A continuación vamos a ver los tipos de rectas que existen en el sistema diédrico. Veremos sus características más importantes como su posición con respecto a los planos de proyección o qué trazas pueden tener, entre otras.
¡Empezamos!
Si has llegado hasta aquí es no entiendes el sistema diédrico y es muy probable que necesites clases de sistema diédrico online. Si después de leer esto, quieres seguir aprendiendo paso a paso y desde cero, en una plataforma donde tengas todo explicado, con ejercicios resueltos y alguien que te resuelva tus dudas, solo tienes que apuntarte al Curso de Sistema Diédrico Online:
VER CURSO DE SISTEMA DIÉDRICO ONLINE
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar sistema diédrico. Puedo explicarte paso a paso cualquier duda que no entiendas.
Sólo tienes que dejarte guiar y verás como vas a aprendiendo poco a poco a resolver tus ejercicios de sistema diédrico.
Rectas en el sistema diédrico
Recta oblicua en el sistema diédrico
La recta oblicua o genérica es una recta que corta a ambos planos de proyección, tanto al plano vertical como al plano horizontal. Algo es oblicuo cuando no es ni perpendicular ni paralelo:
En este caso, la recta se representa de la siguiente forma en sistema diédrico:
Las proyecciones de la recta oblicua forman ángulos diferentes con la línea de tierra.
La recta oblicua, al cortar a ambos planos tiene las dos trazas: la horizontal y la vertical.
Recta horizontal en sistema diédrico
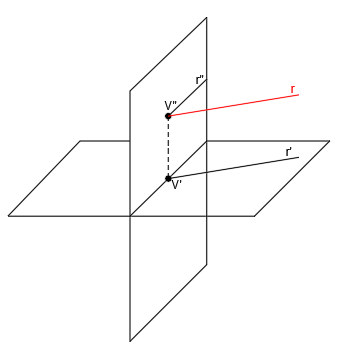
La recta horizontal es una recta paralela al plano horizontal y oblicua al plano vertical:
Que representada en el sistema diédrico nos queda:
La proyección horizontal de esta recta , r’, nos permite tomar medidas reales, ya que al ser la recta paralela al plano horizontal, está en verdadera magnitud. En esta proyección también podemos obtener el ángulo que forma la recta con el plano vertical en verdadera magnitud.
La proyección vertical, r», es paralela a la línea de tierra.
La recta horizontal solo tiene traza vertical, ya que al ser paralela al plano horizontal nunca lo van a intersecar.
Recta paralela a la línea de tierra en sistema diédrico
La recta paralela a la línea de tierra son también paralelas a los planos de proyección horizontal y vertical:
Así que sus dos proyecciones, r» y r’ son paralelas a la línea de tierra.
Su representación en el sistema diédrico queda de la siguiente manera:
La recta se encuentra en verdadera magnitud en cualquiera de las dos proyecciones, debido a ser paralelas a los planos de proyección.
Las rectas paralelas a las líneas de tierra nunca cortan a los planos de proyección, por lo que no tienen trazas y por tanto, nunca cambian de cuadrante.
Sólo se representará en línea continua si se encuentra en el primer cuadrante o contenida en alguno de los planos. Si se encuentra en otro cuadrante, se representará en línea discontinua, además de tener en cuenta que la ubicación de sus proyecciones serán la que corresponda según el cuadrante.
Recta de punta en sistema diédrico
La recta de punta es una recta paralela al plano horizontal y al mismo tiempo es perpendicular plano vertical:
En el sistema diédrico se representa de la siguiente manera:
La proyección horizontal r’ es perpendicular a la línea de tierra, que es donde se aprecia que la recta es perpendicular al plano vertical. La recta se encuentra en verdadera magnitud en esta proyección, por lo que se pueden tomar medidas reales en la misma.
La proyección vertical de la recta, r», se ve como un punto, ya que es perpendicular al plano vertical.
Las rectas de punta solamente cortan al plano vertical, por lo que sólo tienen la traza vertical, que además coincide con su proyección en ese plano.
Las rectas de punta pueden estar por encima o por debajo del plano horizontal o contenidas en él.
Recta frontal en sistema diédrico
La recta frontal es una recta que es paralela al plano de proyección vertical y oblicua al plano de proyección horizontal:
Se representa de la siguiente forma en el sistema diédrico:
Su proyección horizontal r’ es paralela a la línea de tierra.
La proyección vertical de la recta frontal r» se encuentra en verdadera magnitud por ser la recta paralela a este plano y también se puede apreciar el ángulo en verdadera magnitud que forma la recta con el plano de proyección horizontal.
La recta frontal solamente corta al plano horizontal, por lo que solamente tiene traza horizontal.
Las rectas frontales pueden estar por delante o por detrás del plano vertical o contenidas en él.
Recta vertical en sistema diédrico
La recta vertical es una recta paralela al plano vertical y perpendicular al plano horizontal:
En el sistema diédrico queda representada así:
La proyección vertical r» es perpendicular a la línea de tierra, que es donde se aprecia que la recta es perpendicular al plano horizontal. En esta proyección, la recta se encuentra en verdadera magnitud, por lo que es posible tomar medidas reales de la recta.
La proyección horizontal de la recta, r’, queda representada como un punto, al ser perpendicular al plano horizontal.
Las rectas verticales solo cortan al plano horizontal, por lo que sólo tienen la traza horizontal, que además coincide con su proyección en ese plano.
Las rectas verticales pueden estar por delante o por detrás del plano vertical o contenidas en él.
Recta de perfil en sistema diédrico
Las rectas de perfil son rectas oblicuas a los planos de proyección y a su vez, son paralelas a los planos de perfil, que son planos perpendiculares a los planos de proyección horizontal y vertical:
Su representación en sistema diédrico es:
Tanto la proyección vertical r», como la proyección horizontal r’, son perpendiculares a la línea de tierra y ambas se encuentran alineadas en la misma vertical.
Esta recta corta al plano vertical y al plano horizontal, por lo que tiene traza horizontal y vertical.
Si no sabemos las trazas de una recta de perfil y las queremos determinar, necesitamos al menos dos puntos de la recta:
Una vez conocemos dos puntos de la recta, existe un procedimiento que consiste en abatir el plano de perfil que las contiene sobre el plano vertical, siendo la traza vertical donde corte la recta abatida a la proyección vertical de la recta y la traza horizontal abatida, donde la recta abatida corte a la línea de tierra. Veremos más adelante con todo detalle en qué consiste abatir un plano:
La recta abatida se encuentra en verdadera magnitud y nos permite tomar medidas así como determinar los ángulos que forma la recta con los planos de proyección.
Recta contenida en el primer bisector en sistema diédrico
La recta contenida en el primer bisector es oblicua a los planos de proyección horizontal y vertical:
Su representación en diédrico es:
Los puntos pertenecientes a esta recta tienen igual cota que alejamiento, tanto en valor absoluto como en signo. Las proyecciones de esta recta se cortan en la línea de tierra en un único punto y forman el mismo ángulo con ella.
Tanto la traza vertical como la traza horizontal coinciden en el punto que las proyecciones cortan a la línea de tierra.
Recta contenida en el segundo bisector en sistema diédrico
La recta contenida en el segundo bisector es oblicua a los planos de proyección horizontal y vertical:
Su representación en diédrico es:
Los puntos que pertenecen a esta recta tienen igual cota que alejamiento en valor absoluto, pero con signo opuesto. Las proyecciones de esta recta se cortan en la línea de tierra en un único punto y forman el mismo ángulo con ella. En este caso las proyecciones están superpuestas
Tanto la traza vertical como la traza horizontal coinciden en el punto que las proyecciones cortan a la línea de tierra.
¿Necesitas clases de sistema diédrico? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para entender cualquier concepto de sistema diédrico.
He diseñado un método práctico y efectivo que te ayudará a entender cómo resolver ejercicios de sistema diédrico, paso a paso, explicándote justo lo que necesitas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios de sistema diédrico y lo más importante, sabrás por qué se dan esos pasos.
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando información por Internet si puedes aprenderlo en menos de 20 minutos?
Te explicaré lo que necesitas aprender para entender el sistema diédrico. ¿Quieres informarte de como puedes aprender sistema diédrico? Pulsa el botón para saber más:
VER CURSO DE SISTEMA DIÉDRICO ONLINE