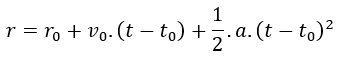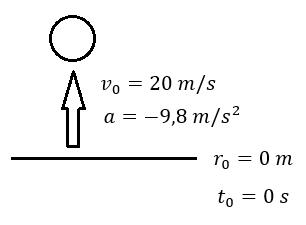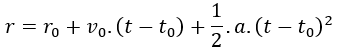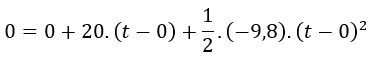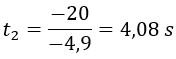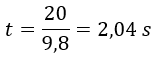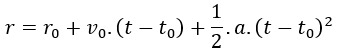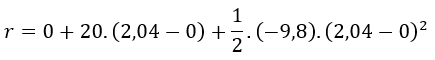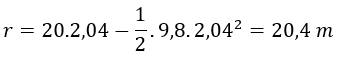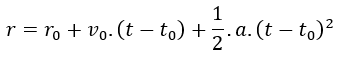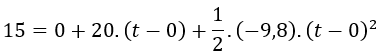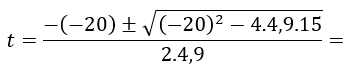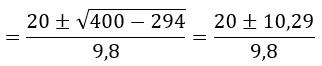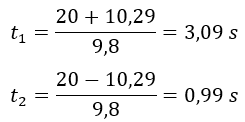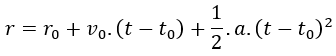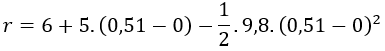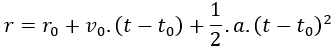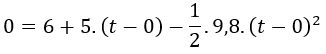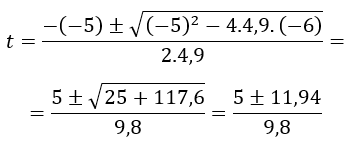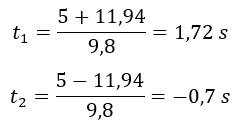A continuación, te voy a enseñar cómo resolver ejercicios de tiro vertical y caída libre. Veremos qué fórmulas se utilizan y las aplicaremos para resolver los ejercicios paso a paso.
¡Empezamos!
Si has llegado hasta aquí es porque buscas ayuda para resolver algún problema de física y necesitas clases de física online y es muy probable que también necesites refuerzo en matemáticas. Si después de leer esto, quieres seguir aprendiendo paso a paso, en una plataforma donde tengas todo explicado, con ejercicios resueltos y alguien que te resuelva tus dudas, solo tienes que apuntarte a los Cursos de Física Online:
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas y física. Puedo explicarte paso a paso cualquier duda que no entiendas.
Sólo tienes que dejarte guiar y verás como vas a aprendiendo poco a poco a resolver tus problemas de física
Tiro vertical y caída libre
Antes de empezar a resolver ejercicios sobre tiro vertical y caída libre, vamos a definir estos dos movimientos y en qué se caracterizan.
¿Qué es el tiro vertical y la caída libre?
El tiro vertical y la caida libre son dos tipos de movimiento que se encuentran dentro de la categoría del movimiento rectilíneo uniforme acelerado, ya que actuan bajo la influencia de una aceleración constante, que en este caso es la aceleración de la gravedad. Además, se caracterizan por producirse en el eje vertical. En ambos tipos de movimientos se considera que no existe ningún tipo de fuerza de rozamiento.
El tiro vertical se caracteriza por realizarse en el eje vertical, hacia arriba, es decir, en sentido contrario a la aceleración de la gravedad, empezando con una determinada velocidad inicial. La velocidad del cuerpo va disminuyendo con el tiempo, al tener sentido contrario a la aceleración, hasta alcanzar el punto más alto, donde tendrá velocidad nula, momento en el que empezará a caer hacia abajo y en el que comienza la caída libre.
La caída libre también se realiza en el eje vertical, hacia abajo, en el mismo sentido a la aceleración de la gravedad, por lo que la velocidad del cuerpo va aumentando con el tiempo. El cuerpo comienza desde el reposo, es decir, con una velocidad igual a cero y se deja caer libremente,
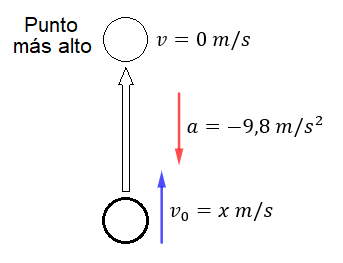
Tanto en el tiro vertical como en la caída libre, la aceleración es constante, que corresponde a la gravedad cuyo valor es de -9,8 m/s² (es negativo ya que su sentido es negativo en el eje y).
Fórmulas de tiro vertical y caída libre
En el tiro vertical y la caída libre se utilizan las fórmulas de velocidad y posición del movimiento rectilíneo unificome acelerado, pero con la particularidad de que ya conocemos el valor de la aceleración (-9,8 m/s²) y sabemos cuándo la velocidad es nula dependiendo si es tiro vertical o caída libre, que veremos detenidamente en los ejercicios resueltos.
Vamos a recordar aquí las fórmulas:
Fórmula de la velocidad del MRUA
donde:
- v = Velocidad final (m/s)
- vo = Velocidad inicial (m/s)
- a = Aceleración (m/s²)
- t = Tiempo final (s)
- to = Tiempo inicial (s)
Fórmula de la posición del MRUA
donde:
- r = Posición final (m)
- ro = Posición inicial (m)
- vo = Velocidad inicial (m/s)
- t = Tiempo final (s)
- to = Tiempo inicial (s)
- a = Aceleración (m/s²)
Ejercicios resueltos de tiro vertical y caída libre
Ejercicio 1
Se lanza una pelota hacia arriba con una celeridad inicial de 20 m/s:
a) ¿Cuánto tiempo está en el aire?
b) ¿Hasta qué altura sube?
c) ¿En qué instante está la pelota a 15 metros del suelo?
d) Tres segundos después de ser lanzanda, ¿la pelota está subiendo o bajando?
En primer lugar, realizamos un esquema con los datos del ejercicio. La posición inicial de la pelota antes de ser lanzada es igual a 0 m en un tiempo inicial de 0 s. La velocidad inicial de la pelota es de 20 m/s y el valor de la aceleración de la gravedad es -9,8 m/s²:
Lo primero que nos preguntan es cuanto tiempo está la pelota en el aire, es decir, el tiempo que la pelota tarda en subir y bajar de nuevo hasta tocar el suelo. Así que, cuando la pelota toque de nuevo el suelo, volverá a su posición inicial, por lo que la posición final de la pelota también es 0 m:
Con estos datos, aplicarmos la fórmula de la posición:
Sustituimos posición inicial, posición final, tiempo inicial y aceleración por sus valores:
Nos queda una ecuación que depende de t, que es el tiempo final y es lo que queremos resolver. Así que vamos a despejarla.
Primero operamos para simplificar:
Tenemos una ecuación de segundo grado, que se resuelve sacando factor común a la t, por no tener término independinte:
Al ser un producto cuyo resultado es cero, por un lado tenemos que por t puede ser igual a 0 (primer resultado de la ecuación):
O que el interior del paréntesis puede ser igual a 0:
De donde despejamos la t obteniendo el segundo resultado de la ecuación:
Tenemos dos resultados: cuando t es igual a 0 s y cuando t es igual a 4,08 s.
En ambos valores del tiempo, la pelota se encuentra en el suelo, pero en t=0 s, la pelota todavía no se ha lanzado y en t=4,08 s, la pelota ya ha subido y ha vuelto a bajar.
Así que, contestando a la pregunta, la pelota se encuentra 4,08 s en el aire.
Nos preguntan también que hasta qué altura sube.
Sabemos que en el punto más alto del tiro vertical, la velocidad del cuerpo es nula:
Lo que no sabemos es el tiempo que tarda la pelota en alcanzar el punto más alto. Así que aplicamos la fórmula de la velocidad sabiendo que la velocidad final es 0 m/s, la velocidad inicial es 20 m/s y la aceleración es es -9,8 m/s²:
Operamos:
Y despejamos t:
La pelota alcanzará el punto más alto a los 2,04 segundos.
Ahora que conocemos el tiempo que tarda en llegar al punto más alto, vamos a aplicar la fórmula de la posición para saber qué valor tiene el punto más alto:
La posición inicial es 0 m, la velocidad inicial es 20 m/s, el tiempo final es 2,04 s, el tiempo inicial es 0 s y la aceleración es -9,8 m/s²:
Operamos:
El punto más alto de la pelota es cuando alcanza los 20,4 metros.
Nos preguntan también en qué instante está la pelota a 15 metros del suelo, es decir, el tiempo que tarda la pelota en alcanzar la posición final de 15 m:
Aplicamos la fórmula de la posición y sustituimos valores:
Operamos para simplificar:
Nos queda una ecuación de segundo grado que pasamos a resolver:
Cuyas soluciones son:
Por tanto, cuando t=0,99 s y cuando t=3,09 s, la pelota estará a 15 m del suelo. Pero, ¿por qué tenemos dos valores de t?
En uno de ellos la pelota está subiendo y en otro la pelota está bajando. Como partimos del suelo, el menor valor de los dos, t=0,99 s, corresponde al tiempo cuando la pelota está subiendo. Después la pelota sigue subiendo hasta su punto más alto y empieza a caer y cuando t=3,09 s la pelota vuelve a estar a 15 m, pero está bajando.
Otra forma de saber si la pelota sube o baja es susituyendo el tiempo final en la fórmula de la velocidad y calcular la velocidad ya que conocemos el resto de datos de la fórmula:
Si la velocidad es positiva, la pelota está subiendo, ya que su sentido coindicide con el sentido positivo del eje «y» y si la velocidad es negativa, la pelota está bajando, porque coindicide con el sentido negativo del eje «y».
Por tanto, sustituimos el tiempo final en la ecuación de la velocidad. Para t=0,99 s, la velocidad es positiva, por lo que está subiendo:
Y para t=3,09 s, la velocidad es negativa, por lo que está bajando:
Por último, nos preguntan si la pelota está subiendo o bajando 3 s después de lanzarse.
Como acabamos de ver, sólo tenemos que susituir t por 3 en la fórmula de la velocidad y operar:
Como la velocidad es negativa, entonces está bajando.
Otra forma de razonarlo sería que como sabemos que la pelota alcanza su punto más alto a los 2,04 s y a partir de ahí al pelota empieza a bajar y t=3 s es mayor a ese tiempo, la pelota está bajando.
Ejercicio 2
Una carga de ladrillos sube mediante una grúa, con una celeridad constante de 5 m/s. A 6 m del suelo se desprende un ladrillo:
a) ¿Cuál es la altura máxima respecto al suelo que alcanza el ladrillo?
b) ¿Cuánto tiempo tarda en llegar al suelo?
c) ¿Qué velocidad lleva en el momento de chocar contra el suelo?
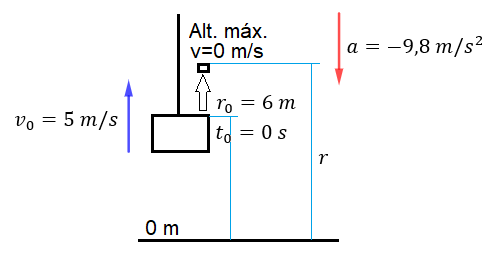
Realizamos un esquema con los datos del problema para entenderlo mejor.
La carga de ladrillos sube con una velocidad de 5 m/s y cuando está a 6 m del suelo un ladrillo se desprende de la carga, momento en que tomaremos el tiempo inicial de 0 s. En ese momento, la posición inicial del ladrillo es de 6 m. A partir de entonces, ese ladrillo seguirá subiendo durante un tiempo con una velocidad inicial de 5 m/s, hasta que llegue al punto más alto, donde su velocidad será 0 m/s y a partir de ese momento, empezará a bajar hasta llegar al suelo. El valor de la aceleración de la gravedad es -9,8 m/s²:
Vamos a empezar calculando la altura máxima que alcanzará el ladrillo.
En su punto más alto, la velocidad del ladrillo es nula:
Tenemos que saber el tiempo que el ladrillo sigue subiendo, que lo hacemos aplicando la fórmula de la velocidad en el punto más alto:
Sabemos que la velocidad final es 0 m/s, la velocidad inicial es 5 m/s, el tiempo inicial es 0 s y la aceleración es -9,8 m/s²:
Operamos y despejamos el valor de t:
Por tanto el ladrillo seguirá subiendo 0,51 s.
Ahora vamos a calcular la posición del ladrillo transcurridos 0,51 s, teniendo en cuenta que la posición inicial del ladrillo es 6 m. Aplicamos la fórmula de la posición y sustituimos todos los valores conocidos:
Operamos, obteniendo el valor de la posición final del ladrillo en el tiempo t=0,51 s (punto más alto):
La altura máxima que alcanzará el ladrillo es de 7,27 m.
Después nos preguntan cuánto tiempo tarda el ladrido en llegar al suelo, es decir, cuándo su posición es igual a 0 m:
Aplicamos la fórmula de la posición:
Y sustituimos los parámetros conocidos por sus valores, como son la posición inicial (6 m), la velocidad inicial (5 m/s), el tiempo inicial (0 s) y la aceleración (-9,8 m/s²):
Operamos para simplificar:
Y resolvemos la ecuación de segundo grado para despejar el valor de t:
Obtenemos dos valores de t: t=1,72 s y t=-0,7 s. El valor de -0,7 s lo deshechamos ya que no existen los valores de tiempo negativos. Así que, desde que el ladrillo se desprende pasan 1,72 s hasta que toca el suelo.
La fórmula ya tiene en cuenta que el ladrillo sigue subiendo durante un tiempo (0,51 s) y luego baja hasta llegar al suelo.
Por último, tenemos que calcular la velocidad del ladrillo justo en el momento que toca el suelo.
Para ello, aplicamos la fórmula de la velocidad:
En este caso, conocemos los valores de la velocidad inicial (5 m/s), la aceleración (-9,8 m/s²), el tiempo cuando el ladrillo toca el suelo (t=1,72 s) y el tiempo inicial (t=0 s). Sustituimos:
Y operamos:
La velocidad tiene sentido negativo, ya que el ladrillo está bajando y por tanto el sentido de la velocidad coindice con el sentido negativo del eje «y».
Ejercicios propuestos de tiro vertical y caída libre con la solución
Ejercicio 1
Una paracaidista se tira desde un precipicio y cae 50 m libremente en el aire. Abre el paracaídas y su aceleración pasa tener un valor de 2 m/s², llegando al suelo con una velocidad de -3 m/s. Calcula cuánto tiempo estuvo el paracaidista en el aire y desde qué altura saltó.
Ejercicio 2
Se lanza un cuerpo hacia arriba verticalmente desde un punto alto situado a 28 m del suelo. El cuerpo llega al suelo 3 s después de haber sido lanzando. Calcula:
a) La velocidad con la que fue lanzado
b) La velocidad con la que llega al suelo
c) Altura a la que sube
¿Necesitas ayuda en física y matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para entender física y las matemáticas que necesitas aplicar.
He diseñado un método práctico y efectivo que te ayudará a entender la física así como las matemáticas que necesitas aplicar, paso a paso, explicándote justo lo que necesitas para saber resolver todos problemas y saber aplicar las fórmulas que correspondan. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus problemas de física
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando información por Internet si puedes aprenderlo en menos de 20 minutos?
Te explicaré lo que necesitas aprender para entender física y las matemáticas que necesitas aplicar. ¿Quieres informarte de como puedes aprender física y matemáticas? Pulsa el botón para saber más: