A continuación vamos a estudiar a fondo todo lo relativo al triángulo: Definición de triángulos, propiedades, construcción de triángulos, clasificación y tipos de triángulos según sus lados y sus ángulos y también veremos cómo calcular tanto el perímetro como el área de un triángulo, con ejercicios resueltos paso a paso.
Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Definición de triángulo
¿Qué es un triángulo?
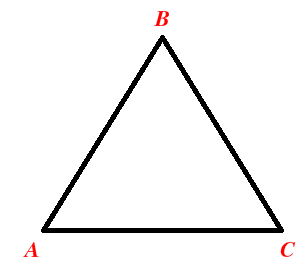
Un triángulo es un polígono de 3 lados y 3 vértices. En cada vértice se unen 2 lados, que forman un ángulo entre ellos:
A los vértices, se les suele llamar con letras mayúsculas A, B y C:
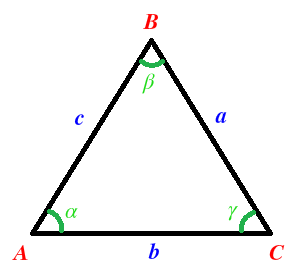
A los lados, se les suele llamar con letras minúsculas, a, b y c y se nombran en función del nombre del vértice, de forma que se le llama con la misma letra al lado que está enfrente de cada vértice:
Por último, a los ángulos se nombran de la misma forma que los vértices pero con letras griegas: α, β y γ
Propiedades de los triángulos
Los triángulos tienen las siguientes propiedades que se cumplen siempre:
- Cualquier lado es siempre menor que la suma de los otros dos:
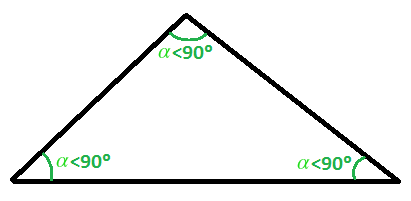
- La suma de los ángulos de un triángulo suman 180º:
Ambas propiedades son muy importantes a la hora de resolver ejercicios con triángulos, así como para construir e identificar triángulos.
Construcción de triángulos. Igualdad de triángulos
Si en un triángulo conocemos los tres lados y los tres ángulos, no tendremos ningún problema para identificarlo o para construirlo.
Pero, ¿son necesarios todos los datos? ¿Qué datos necesitamos para determinar un triángulo?
Un triángulo queda determinado en los siguientes casos:
- Cuando se conocen las longitudes de los tres lados
Vamos a ver cómo se construye un triángulo conocidos los tres lados con un ejemplo:
Construye un triángulo cuyos lados midan 3, 4 y 6 cm.
Colocamos el lado de 6 cm como base (por ejemplo, ya que podemos colocar cualquiera) y con un compás realizamos un arco de radio 4 cm y centro en uno de los dos extremos (por ejemplo, yo lo he hecho en el lado izquierdo). Con centro en el otro extremo, realizamos otro arco de radio 3 cm:
El punto donde se corten los dos arcos corresponderá al tercer vértice del triángulo. Uniendo cada extremo de la base con el punto de corte, obtendremos nuestro triángulo:
- Cuando se conocen un lado y sus dos ángulos contiguos
Vamos a ver cómo construir un triángulo sabiendo que uno de los lados mide 7 cm y los ángulos contiguos 60º y 30º.
Colocamos el lado como base y en uno de los extremos realizamos una línea con un ángulo de 60º, por medio de un transportador de ángulos. En el extremo opuesto dibujamos otra línea con un ángulo de 30º:
El punto donde se unen las dos líneas corresponde al tercer vértice, por lo que solo tenemos que unir ese punto con los extremos del lado para terminar de construir el triángulo:
- Cuando se conocen dos lados y el ángulo comprendido entre ellos.
Vamos a ver cómo construir un triángulo conocidos dos lados y el ángulo comprendido entre ellos con un ejemplo:
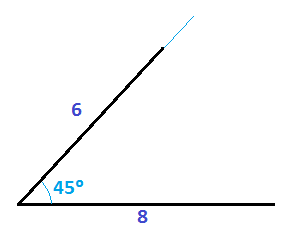
Dibuja un triángulo sabiendo que un lado mide 8 cm, otro lado mide 6 cm y forman un ángulo de 45º:
Colocamos uno de los dos lados de base, yo por ejemplo he elegido el de 8 cm y en uno de los dos extremos realizamos una línea con una inclinación de 45º, gracias al transportador de ángulos:
Sobre la línea que acabamos de hacer, dibujamos el segundo lado con una longitud de 6 cm, ayudándonos de una regla:
Para terminar el triángulo, unimos los dos extremos que nos quedan libres:
Por tanto, sabiendo los casos en los que un triángulo queda determinado, podemos afirmar que dos triángulos son iguales si tienen:
- Los tres lados iguales
- Un lado y sus dos ángulos contiguos iguales
- Dos lados y el ángulo comprendido entre ellos iguales.
Rectas y puntos notables del triángulo
Vamos a ver ahora las rectas y puntos notables de un triángulo:
Mediatriz
La mediatriz es la recta perpendicular a un lado que pasa por su punto medio:
Las tres mediatrices de un triángulo coinciden en un punto llamado circuncentro. El circuncentro está a la misma distancia de los tres vértices y por tanto es el centro de la circunferencia circunscrita:
Bisectriz
La bisectriz es una semirrecta que divide a un ángulo en dos partes iguales:
Las tres bisectrices de un triángulo coinciden en un punto llamado incentro. El incentro de un triángulo está a la misma distancia de los tres lados, por lo que es el centro de la circunferencia inscrita:
Mediana
La mediana es un segmento que une cada vértice con el punto medio del lado opuesto:
Las tres medianas de un triángulo coinciden en un punto llamado baricentro (G). La distancia del baricentro a cada vértice es el doble que al punto medio del correspondiente lado opuesto:
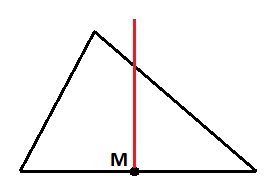
Altura
La altura es un segmento perpendicular a un lado desde el vértice opuesto. A la altura de un triángulo la llamamos h y la utilizamos para calcular su área:
Las tres alturas de un triángulo se cortan en un punto llamado ortocentro:
Tipos de triángulos
Ahora vamos a ver los tipos de triángulos que existen. La clasificación de triángulos se puede realizar según sus lados y según sus ángulos.
Clasificación de triángulos según sus lados
Esta forma de clasificar los triángulos se basa en el número de lados iguales que tenga el triángulo. El número de ángulos iguales coincidirá con el número de lados iguales.
Triangulo equilátero
El triángulo equilátero tiene los tres lados iguales y como consecuencia, los tres ángulos iguales, los cuales miden 60º:
Triangulo isósceles
El triángulo isósceles tiene dos lados iguales y por tanto, dos de sus ángulos también son iguales:
Triangulo escaleno
El triángulo escaleno no tiene ningún lado igual y como consecuencia, todos sus ángulos son distintos:
Clasificación de triángulos según sus ángulos
Otra forma de clasificar los triángulos es según el valor de sus ángulos. Vamos a verlo:
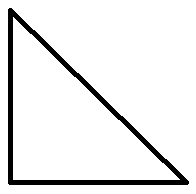
Triángulo rectángulo
El triángulo rectángulo tiene un ángulo recto, es decir, de 90º, teniendo los otros dos ángulos agudos, es decir, menores de 90º. Los ángulos rectos se suelen marcar con un cuadrado:
Triángulo acutángulo
El triángulo acutángulo es el que tiene todos su ángulos agudos, es decir, menores de 90º:
Triángulo obtusángulo
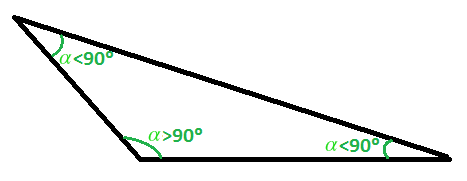
El triángulo obtusángulo tiene uno de sus ángulos obtuso, es decir, mayor de 90º y los otros dos ángulos son agudos:
Tanto los triángulos acutángulos como los triángulos obtusángulos son a su vez triángulos oblicuángulos, que son los triángulos que no tienen ningún ángulo recto.
Tipos de triángulos según sus lados y sus ángulos
Acabamos de ver que los triángulos se pueden clasificar según sus lados o según sus ángulos, pero además, ambas clasificaciones se pueden combinar entre sí.
Triángulo rectángulo isósceles
Un triángulo rectángulo isósceles es el que tiene un ángulo recto y además dos lados iguales:
Triángulo rectángulo escaleno
Un triángulo rectángulo escaleno, tiene un ángulo recto y los tres lados de distinta longitud:
Triángulo acutángulo equilátero
Un triángulo acuángulo es equilátero cuando todos sus lados y ángulos son iguales:
Triángulo acutángulo isósceles
Un triángulo acutángulo isósceles es aquel que tiene todos los ángulos agudos y dos lados iguales:
Triángulo acutángulo escaleno
El triángulo acutángulo escaleno tiene todos sus ángulos agudos pero ninguno de sus lados son iguales:
Triángulo obtusángulo isósceles
El triángulo obtusángulo isósceles tiene un ángulo mayor de 90º y dos lados iguales:
Triángulo obtusángulo escaleno
El triángulo obtusángulo escaleno es aquel que tiene un ángulo mayor de 90º y ningún lado igual:
Cómo calcular el perímetro de un triángulo
El perímetro de un triángulo es la suma de los tres lados:
En un triángulo equilátero, como los tres lados son iguales, el perímetro coincide con el triple de la longitud de uno de sus lados:
El perímetro de un triángulo isósceles, al tener dos lados iguales es:
El perímetro de un triángulo es una longitud, por tanto se mide en unidades lineales, es decir, mm, cm, m, etc y además de mide en la misma unidad que los lados.
Por ejemplo, vamos a calcular el perímetro del siguiente triángulo:

Como los lados estaban en cm, el perímetro también está en cm.
Cómo calcular el área de un triángulo
El área de un triángulo se calcula con la siguiente fórmula, que se lee: área es igual a base por altura partido por dos:
El área se mide en unidades cuadradas (mm², cm², m²…). Su unidad será la misma que la de los lados pero elevada al cuadrado.
Si nos dan tanto la base como la altura del triángulo el área de calcula fácilmente aplicando la fórmula anterior. Por ejemplo: Calcular el área de un triángulo de base 5 cm y de altura 3 cm.
Sustituimos el área y la altura por su valor en la fórmula y nos queda:
Observa que el resultado está en cm² ya que los lados están en cm.
Cálculo de la altura de un triángulo
En triángulos rectángulos, uno de sus lados coincide con la altura, pero si el triángulo no es rectángulo y no nos dan el valor de la altura, debemos calcularla.
¿Y cómo calculamos la altura de un triángulo?
Para calcular la altura de un triángulo debemos aplicar el teorema de Pitágoras. Vamos a verlo con un ejemplo:
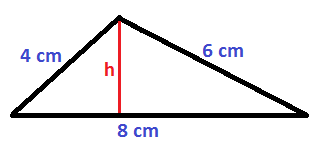
Calcula el área del siguiente triángulo:
El área se calcula con la siguiente fórmula:
En este caso, sabemos que la base mide 8 cm, pero no sabemos cuánto mide la altura. Por tanto, debemos obtener su valor.
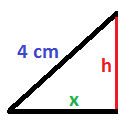
Si te das cuenta, la altura divide al triángulo original en dos triángulos rectángulos. Como no sabemos lo que mide la base de cada uno de estos rectángulos, a una de ellas le llamamos x y la otra por tanto será 8-x, que es el resultado de restar x a los 8 cm que tiene la base total:
El triángulo rectángulo de la izquierda queda de la siguiente forma:
Aplicando el teorema de Pitágoras en este triángulo nos queda la siguiente ecuación:
El triángulo de la derecha nos queda:
Aplicando aquí el teorema de Pitágoras tenemos:
Tenemos por tanto, dos ecuaciones con dos incógnitas, que son h y x:
En el Curso de Sistemas de dos Ecuaciones con dos Incógnitas te explico con todo detalle cómo resolver sistemas de este tipo.
Vamos a resolver el sistema. De la primera ecuación:
Despejo h²:
En la segunda ecuación:
Sustituyo h² por la expresión en función de x que acabamos de obtener:
Desarrollamos los cuadrados de los números y el producto notable:
Los términos con x² se anulan. Dejamos el término con x en el primer miembro y pasamos los números al segundo miembro:
Despejamos la x y resolvemos:
Ya sabemos el valor de x.
Ahora, en la expresión donde despejamos h² :
Sustituimos x por su valor:
Despejamos h, pasando el cuadrado al segundo miembro como raíz y operamos, obteniendo el valor de h:
Ahora que tenemos h, ya podemos calcular el área del triángulo original, que es:
Cuyo resultado se expresa en centímetros cuadrados.
Ejercicios resueltos de triángulos
Vamos a resolver unos ejercicios sobre triángulos aplicando todo lo aprendido.
Ejercicio resuelto 1
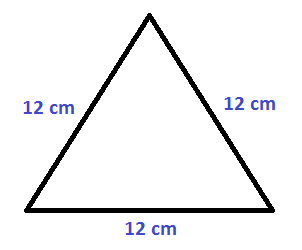
Calcula el área de un triángulo equilátero de 12 cm de lado:
En primer lugar, debemos calcular la altura, que divide al triángulo equilátero en dos triángulos rectángulos cuya base es la mitad que la base del triángulo original:
Calculamos la altura a partir de cualquiera de esos dos triángulos:
Aplicamos Pitágoras y queda:
Despejamos h pasando el cuadrado como raíz al segundo miembro:
Y operamos:
Una vez tenemos la altura, ya podemos calcular el área del triángulo original que es:
Ejercicio resuelto 2
Una finca tiene la forma y dimensiones indicados en la figura. Calcula su área.
Esta fina se divide en dos triángulos. El área total será la suma de cada triángulo.
El primer triángulo se trata de un triángulo isósceles, del cual no conocemos la altura, pero la calculamos a partir de los triángulos rectángulos que se forman:
Aplicamos Pitágoras en uno de ellos:
Despejamos h:
Y operamos:
El área de este triángulo es:
Ahora vamos con el área del segundo triángulo:
Este triángulo se trata de un triángulo rectángulo, ya que tiene un ángulo recto. Para que se vea más claro,lo giramos un poco:
En este caso, la base vale 30 m y la altura 40 m, por lo que su área es:
El área total de la finca es la suma de las dos áreas anteriores:
¿Necesitas ayuda en matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: