Valores característicos de una onda senoidal en corriente alterna. Ejercicios

A continuación vamos a ver qué es una onda senoidal y vamos a definir y explicar los valores característicos de una onda senoidal, aplicándolo a las ondas de corriente alterna, como son la tensión, la intensidad y la potencia. Resolveremos ejercicios sobre ondas senoidales para que te quede todo más claro.

¡Empezamos!

Si has llegado hasta aquí es porque hay algún ejercicio que no sabes resolver y necesitas clases de electrotecnia online y es muy probable que también necesites refuerzo en matemáticas. Si después de leer esto, quieres seguir aprendiendo paso a paso, en una plataforma donde tengas todo explicado, con ejercicios resueltos y alguien que te resuelva tus dudas, solo tienes que apuntarte a los Cursos de Electrotecnia Online:

VER CURSOS DE ELECTROTECNIA ONLINE

Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas y electrotecnia. Puedo explicarte paso a paso cualquier duda que no entiendas.

Sólo tienes que dejarte guiar y verás como vas a aprendiendo poco a poco a resolver tus ejercicios de electrotecnia.

Qué es una onda senoidal

Una onda senoidal es una función que depende del seno. Si tomamos por ejemplo una onda senoidal de tensión, su fórmula tiene la siguiente forma:

donde:

• Vmáx es el valor máximo
• w es la velocidad angular
• t es el tiempo

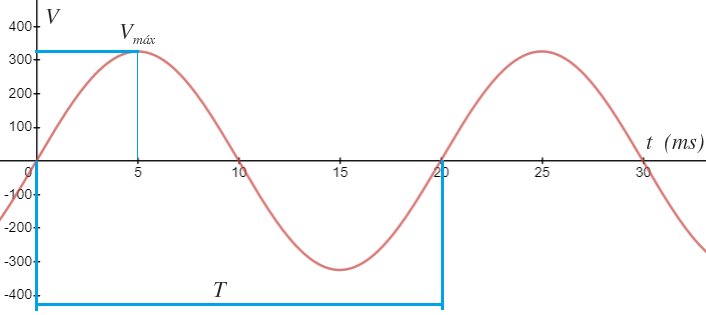
Si representamos la función senoidal nos queda la siguiente gráfica:

Lo que veamos para esta onda, también es aplicable a ondas senoidales de intensidad, cuyas fórmula es:

Valores característicos de una onda senoidal

Vamos a ver más en detalle los valores característicos de una onda senoidal.

Fase (φ)

La fase de una onda es igual al instante en el que se analiza su valor. En la fórmula, es el contenido del seno:

Es útil cuando nos dan el valor de la fase, ya que directamente nos están dando el valor de la velocidad angular por el tiempo.

Cuando nos dan la fase, la fórmula de la onda tiene esta forma:

Periodo (T)

Una onda senoidal, es una función periódica, es decir, que se va repitiendo cada ciertos tiempo, completando lo que se llama un ciclo. Al tiempo que tarda la onda en realizar un ciclo se le llama periodo y se representa como T.

El periodo se mide en segundos (s)

En nuestro ejemplo, T=20 ms, lo que quiere decir que la forma de la onda senoidal se repita cada 20 ms.

Frecuencia (Hz)

La frecuencia es el número de ciclos que la onda realiza en un segundo. Es la inversa del periodo y se mide en Hercios:

Velocidad angular (w)

La velocidad angular es la velocidad a la que gira la bobina del alternador que induce la corriente alterna. Se calcula como el ángulo recorrido en un ciclo (2π) partido por el periodo:

Se mide en radianes/segundo.

Como la frecuencia es la inversa del periodo, la velocidad angular también se puede calcular como el ángulo recorrido en un ciclo (2π) multiplicado por la frecuencia:

Valor máximo

Es el valor más elevado que puede alcanzar la onda senoidal, también conocido como amplitud, valor pico o valor cresta.

El valor máximo multiplica al seno en la fórmula de la función senoidal:

El valor máximo se alcanza en el momento que el seno de la velocidad angular por el tiempo es igual a 1:

ya que de esta manera, la amplitud queda multiplicada por 1:

El seno es igual a 1 cuando w.t es igual a π/2 radianes:

En la gráfica del ejemplo, corresponde con los picos de la onda.

Valor instantáneo

El valor instantáneo es el valor que toma la onda en un instante de tiempo determinado t.

Por ejemplo, ¿qué valor tomaría la tensión del ejemplo cuando t=0,003 s, sabiendo que la tensión máxima es 325 V y la frecuencia es igual a 50 Hz?

La función de la tensión del ejemplo es:

La tensión máxima es 325 V:

Y a partir del dato de la frecuencia, calculamos la velocidad angular:

Sustituimos Vmáx y w en la fórmula y queda:

Ahora sólo tenemos que sustituir la t por los 0,003 segundos y operar (recuerda que la calculadora debe estar en radianes):

Valor eficaz

De todos los valores instantáneos que aparecen en una onda senoidal ¿qué valor tomamos de referencia para los cálculos?

Hay que encontrar un valor intermedio que produzca los mismo efectos caloríficos en una carga que un valor equivalente en corriente continua. A este valor se le llama valor eficaz.

Queda demostrado matemáticamente que la relación que existe entre el valor eficaz es igual al valor máximo dividido entre raíz de 2:

El valor eficaz es lo que miden los aparatos de medida y es que se utiliza en la práctica.

En nuestro ejemplo, el valor eficaz correspondiente a la tensión industrial es:

Valor medio

El valor medio es el resultado de realizar la media de todos los valores instantáneos de un semiperiodo. Su valor es igual a 2 veces el valor máximo dividido entre π:

Como una de las mitades del ciclo es negativa respecto a la otra, el valor medio de la corriente alterna es 0 si tomásemos el periodo completo.

En nuestro ejemplo, el valor medio es:

Representación fasorial de una onda senoidal

Las ondas senoidales se pueden representar también mediante fasores, que son vectores rotativos que giran a la velocidad angular w en el sentido contrario a las agujas del reloj (sentido antihorario), con el origen del vector fijo en el origen de coordenadas.

El ángulo que forma el vector con el eje x coincide con el valor del eje x en la onda y el extremo del vector, coincide con el valor de la onda en cada punto. El vector tiene una longitud que es igual al valor máximo de la onda.

De esta forma, podemos representar cada instante de una onda mediante su fasor correspondiente y viceversa.

Por ejemplo, si tenemos un fasor de tensión de módulo 5 y ángulo 60º, ¿cuál sería su ecuación de onda senoidal correspondiente?

La ecuación de una onda senoidal tiene esta forma:

Y la fase es igual a la velocidad angular por el tiempo, es decir, al contenido del seno:

Sustituimos el valor máximo por el módulo del vector y wt por el ángulo y obtenemos su correspondiente ecuación de onda:

Ejercicios resueltos sobre ondas senoidales en corriente alterna

Vamos a resolver unos ejercicios para que queden más claros todos los conceptos que acabamos de ver.

Ejercicio 1

Una onda de intensidad alterna senoidal tiene la siguiente expresión:

Calcular:

a) El valor de la frecuencia

b) El valor del periodo

c) El valor de la intensidad en el instante t=5 ms

d) El valor de la intensidad para 120º

El valor de la frecuencia lo vamos a calcular a partir de la fórmula de la velocidad angular:

De la fórmula deducimos que la velocidad angular es igual a 377 rad/s, luego sustituimos ese valor en la fórmula:

De la ecuación que nos queda, despejamos al frecuencia y operamos:

El periodo, lo calculamos con la siguiente fórmula:

Como conocemos el valor de la frecuencia, sustituimos por su valor y operamos:

Para calcular el valor de la intensidad en el instante t=5 ms, en la fórmula, sustituimos t por 0,005, ya que el tiempo debe estar en segundos para que el resultado sea en amperios.

Sustituimos y operamos (con la calculadora en radianes):

Por último, nos dan el valor de la fase, que es 120º:

Sustituimos este valor en el contenido del seno y operamos (con la calculadora en grados):

Ejercicio 2

Una espira gira a 1500 revoluciones/minuto en el seno del campo magnético formado por un par de polos. ¿Cuál será la velocidad angular, la frecuencia y el periodo de la tensión alterna inducida en la espira?

El enunciado nos dice que la espira gira a 1500 revoluciones por minuto. Ese dato corresponde con la velocidad angular:

Pero debemos pasar las revoluciones/minuto a radianes/segundo para poder calcular el resto de datos y que estos resulten en su unidad correcta.

Para pasar de revoluciones/minuto a radianes/segundo sabemos que 1 revolución es igual a 2π radianes:

y que 1 minuto es igual a 60 segundos:

Si nos fijamos en las unidades, las revoluciones están en el numerador y los minutos en el denominador. Por tanto, multiplicamos las revoluciones por 2π  para pasar de revoluciones a radianes y en el denominador (que es donde están los minutos) multiplicamos por 60 para pasar de minutos a segundos, que es lo mismo que dividir entre 60 y operamos:

Conocida la velocidad angular, podemos obtener la frecuencia ya que la velocidad angular es igual a 2 por π por la frecuencia:

Despejamos la frecuencia:

Sustituimos la velocidad angular por su valor y operamos:

Teniendo el valor de la frecuencia, podemos calcular el valor del periodo ya que el periodo es igual a la inversa de la frecuencia o lo que es lo mismo, 1 entre la frecuencia:

Sustituimos la frecuencia por su valor y operamos:

Ejercicio 3

Una onda de corriente alterna tiene la siguiente expresión:

Calcula el valor medio y el valor eficaz de dicha corriente.

Para calcular el valor medio y el valor eficaz, necesitamos el valor máximo, que es el número que queda multiplicando al seno, es decir, que la intensidad máxima es igual a 24 A.

Calculamos la intensidad media, multiplicando la intensidad máxima por 2 y dividiendo entre π:

La intensidad eficaz la calculamos dividiendo la intensidad máxima entre raíz de 2:

¿Necesitas ayuda en electrotecnia y matemáticas? ¿Quieres que te explique cualquier duda que te surja?

Puedo enseñarte exactamente lo que necesitas aprender para entender electrotecnia y las matemáticas que necesitas aplicar.

He diseñado un método práctico y efectivo que te ayudará a entender la electrotecnia así como las matemáticas que necesitas aplicar, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.

Con mi método:

• Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas de electrotecnia
• Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión

Suena bien ¿no?

¿Por qué tardar 2 horas buscando información por Internet si puedes aprenderlo en menos de 20 minutos?

Te explicaré lo que necesitas aprender para entender electrotecnia y las matemáticas que necesitas aplicar. ¿Quieres informarte de como puedes aprender electrotecnia y matemáticas? Pulsa el botón para saber más:

ENSÉÑAME ELECTROTECNIA