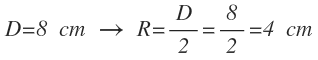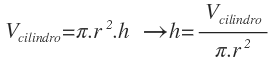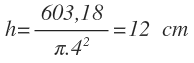A continuación te voy a explicar cómo calcular el volumen de un cilindro y cómo calcular el área de un cilindro. Lo veremos con ejercicios resueltos paso a paso.
Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
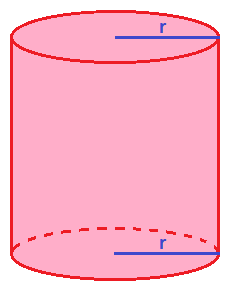
Elementos principales de un cilindro
Vamos a ver los principales elementos de un cilindro. Existen más partes del cilindro, pero éstas son las que necesitas conocer para calcular su área y su perímetro.
Bases de un cilindro
Las bases de un cilindro son los dos círculos que están en la parte superior e inferior del cilindro. Tenemos la base superior y la base inferior. Ambas son iguales y paralelas entre sí.
Superficie lateral de un cilindro
La superficie lateral de un cilindro es la superficie curva del cilindro encerrada entre las dos bases:
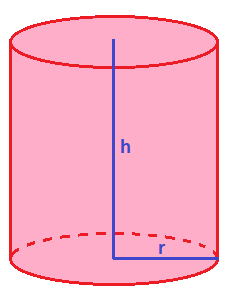
Altura de un cilindtro
La altura de un cilindro es la distancia que hay entre las dos bases del cilindro, medida perpendicularmente:
Radio de un cilindro
El radio de un cilindro corresponde al radio de una de las dos bases, las cuales son círculos, tal y como te he comentado antes:
Cuántas caras tiene un cilindro
Un cilindro tiene 3 caras: las dos bases, que son caras rectas y la superficie lateral que es una cara curva:
Cómo calcular el volumen de un cilindro
Vamos a ver cómo calcular el volumen de un cilindro de altura h y de radio r:
Fórmula del volumen de un cilindro
El volumen de un cilindro se calcula multiplicando el área de la base por la altura del cilindro:
El área de la base corresponde al área de un círculo, por lo que la fórmula del volumen de un cilindro queda:
Donde r es el radio del cilindro y h es su altura. Estos son los dos datos que necesitas para calcular el volumen de un cilindro. Debes tener cuidado en los problemas y asegurarte que se miden en la misma unidad.
El volumen de un cilindro se mide en unidades cúbicas.
Ejemplo de cálculo del volumen de un cilindro
Vamos a ver un ejemplo de cómo calcular el volumen de un cilindro:
Calcular el volumen de un cilindro de radio 3 cm y de altura 80 mm.
En primer lugar, debemos poner tanto el radio como la altura en las mismas unidades. Pasamos la altura de mm a cm:
Una vez tenemos el radio y la altura en las misma unidades, aplicamos la fórmula del volumen de una esfera:
Sustituimos el radio y la altura por sus valores y operamos:
El resultado se mide en cm³, ya que tanto el radio como la altura están en cm en la fórmula.
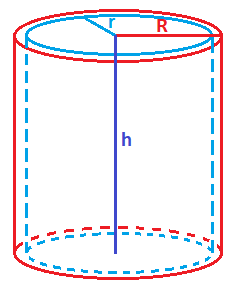
Volumen de un cilindro hueco
Un cilindro hueco es aquel que existe vacío en su interior y tiene una pared de un espesor determinado.
El cilindro hueco tiene dos radios: el radio exterior R, que va desde el centro de la base hasta la superficie exterior del cilindro y el radio interior r, que va desde el centro de la base hasta la superficie interior del cilindro:
El espesor de la pared del cilindro es igual al radio exterior menos el radio interior:
Fórmula del volumen de un cilindro hueco
El volumen de un cilindro hueco es igual al volumen del cilindro exterior de radio R, menos el volumen de la parte vacía, que equivale al volumen de un cilindro interior de radio r:
Ejemplo de cálculo del volumen de un cilindro hueco
Hallar el volumen de un cilindro hueco de 10 mm de radio exterior, 40 mm de altura y 2 mm de espesor:
En el problema nos dan directamente el radio exterior:
Con el dato del espesor, calculamos el radio interior, despejando r en la fórmula del espesor:
La altura es común a los dos cilindros y es igual a 40 mm.
La fórmula del volumen de un cilindro hueco es:
Sustituimos R, r y h por su valor y calculamos:
Desarrollo de un cilindro en un plano
Si ha un cilindro le quitamos las bases, como si de dos tapas se tratasen, cortamos la superficie lateral y la abrimos, nos queda el desarrollo de un cilindro tal y como te muestro a continuación:
Este desarrollo del cilindro sirve para construir cilindros a partir de una superficie plana, además de entender mejor cómo calcular el área de un cilindro.
Cómo calcular el área de un cilindro
Vamos a ver cómo calcular el área de un cilindro de altura h y de radio r:
El área de un cilindro es igual a la suma de las áreas de las dos bases más el área de la superficie lateral:
Tal y como hemos visto en el desarrollo de un cilindro, si abrimos la superficie lateral, corresponde a un rectángulo, cuya base es igual al perímetro de la circunferencia de la base, es decir a 2.π.r y la altura del rectángulo es igual a la altura del cilindro h:
Por tanto, el área lateral es igual al área del rectángulo, de base 2.π.r y de altura h:
Por otro lado, el área de las bases es igual al 2 veces el área de una base, ya que tenemos dos bases:
Como cada base es un círculo, el área de la base es igual al área de un círculo de radio r:
Y por tanto el área de las dos bases es el doble:
Fórmula del área de un cilindro
Concluyendo, el área de un cilindro es la suma del área lateral más el área de las dos bases:
Que sustituyendo cada una por su valor, nos queda:
El área de un cilindro se mide en unidades cuadradas.
No te recomiendo que te aprendas esta fórmula de memoria. Al fin y al cabo, es calcular el área de dos círculos y de un rectángulo, por lo que te aconsejo que lo hagas paso a paso como lo he hecho yo aquí, en vez de aplicar directamente la fórmula.
Ejemplo de cálculo del área de un cilindro
Vamos a ver un ejemplo de cómo calcular el área de un cilindro:
Calcular el área de un cilindro de radio 3 cm y de altura 80 mm.
En primer lugar, igual que hicimos antes, debemos poner tanto el radio como la altura en las mismas unidades. Pasamos la altura de mm a cm:
El área del cilindro es igual al área de la superficie lateral más el área de las bases:
Empezamos calculando el área de la superficie lateral:
El área de la superficie lateral es igual al área de un triángulo de base 2.π.3 y de altura 8:
Calculamos ahora el área de las bases, que es igual al área de una base por 2:
El área de una base es igual al área de un círculo de radio 3:
Sumamos el área lateral y el área de las bases y obtenemos el área del cilindro:
Ejercicios resueltos sobre volumen y área de un cilindro
Ejercicio 1
Halla la altura de un cilindro cuyo diámetro es de 8 cm y su volumen de 603,18 cm³
Calculamos el radio a partir del diámetro, ya que el radio es la mitad del diámetro y queda:
De la fórmula del volumen de un cilindro, despejamos la altura:
Y en la expresión que nos queda, sustituimos el volumen y el radio del cilindro por su valor:
La altura del cilindro es de 12 cm.
Ejercicio 2
Calcula el área del cilindro del ejercicio anterior.
El área de un cilindro es igual al área de la superficie lateral más el área de las bases:
El área de la superficie lateral es:
Sustituimos el radio y la altura por sus valores y operamos:
El área de las bases es:
Sustituimos el radio por su valor y operamos:
Finalmente, el área del cilindro es:
¿Necesitas ayuda en matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: