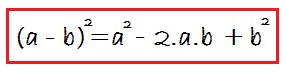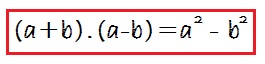Si vous ne vous souvenez jamais d’appliquer les formules spéciales du produit et quand vous vous souvenez, alors vous ne savez pas comment l’appliquer, continuez à lire parce qu’en moins de 5 minutes vos doutes seront résolus.
Multiplier deux polynômes ensemble, s’ils ont plus de trois termes et dans leurs termes ont plusieurs variables, peut être très fastidieux et vous pouvez investir beaucoup de temps à multiplier.
Heureusement, si les polynômes à multiplier sont de deux termes (binômes) et que leurs termes sont égaux, vous pouvez appliquer les formules de produits notables, ce qui vous permettra d’effectuer la multiplication directement.
Aimeriez-vous savoir comment identifier quand vous avez un produit spécial et comment appliquer sa formule ?
Dans ce post, je vais vous expliquer étape par étape les différentes formules de produits spéciaux, avec des exemples résolus étape par étape, afin que vous appreniez à les appliquer dans vos exercices.
Définition des produits spéciaux
Qu’est-ce qu’un produit spécial ?
Les produits spéciaux, sont des polynômes de deux termes (binômes) élevés au carré, ou le produit de deux binômes, comme nous le verrons plus loin, dont le développement suit toujours les mêmes règles.
Ainsi, au moment où vous les identifiez, vous devez appliquer directement leurs formules pour les développer, sans avoir à multiplier terme par terme, pour vous faire gagner du temps et éviter les complications.
Les formules de produit spéciales les plus importantes sont : le carré de la somme, le carré de la différence et la somme par différence ou différence des carrés.
Voyons chacun d’entre eux.
Formules spéciales de produits
Carré de formule de somme
La façon de lire ce produit spécial est : Carré du premier, plus le double du premier par le second, plus le carré du second :
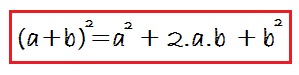
Pour appliquer cette formule, il suffit de remplacer les termes du polynôme par a et b. Par exemple :
Le premier est x et le second est 1. Donc alors :
- Carré du premier : x
- Double du premier par le second : 2. x. 1
- Carré de la seconde : 1
Jusqu’à présent, vous avez appliqué la formule. Maintenant, nous devons agir à l’intérieur de chaque terme pour simplifier, multiplier les nombres et les pouvoirs de résolution :
Une erreur grave est de ne pas se rendre compte que l’expression ci-dessus est un produit spécial et d’équarrir chaque terme incorrectement :
Carré de la formule de différence
Cette formule est très similaire au carré de la formule de la somme, avec la différence du signe moins au second terme.
Il se lit comme suit : Carré du premier, moins deux fois le premier par le second, plus le carré du second :
Comme dans le cas précédent, le premier est «a» (premier terme du polynôme) et le second est «b» (deuxième terme du polynôme). Pour appliquer cette formule, vous n’avez qu’à remplacer les termes du polynôme par a et b.
Par exemple :
- Carré du premier : 2²
- Double du premier par le second : 2.2.x
- Carré de la seconde : x²
Le carré d’une somme et le carré d’une différence peuvent être utilisés pour factoriser les polynômes, appliqués à l’envers, c’est-à-dire, à partir du développement, en obtenant les produits spéciaux.
Différence des carrés de formule
Cette formule est très utile pour factoriser les polynômes et simplifier les fractions algébriques lorsque nous avons la soustraction de deux termes au carré :
Habituellement, la différence de carrés est «camouflée» et n’est pas directement visible, il est donc très important de savoir comment l’identifier.
Par exemple : x²-25 n’est apparemment pas une différence de carrés, parce que nous ne voyons pas le deuxième terme élevé au carré, mais puisque nous savons que 25 est 5² alors nous pouvons appliquer la formule :
>» height=»29
À prendre en compte avec les formules spéciales du produit
Je viens de vous montrer les trois formules des produits spéciaux les plus importants.
Il y a d’autres produits spéciaux comme le cube d’une somme, le cube d’une différence, le cube d’une différence, le carré trinomial…. qui ne sont pas du tout pratiques ou les plus compliqués à mémoriser.
Dans de tels cas, il est préférable de développer la multiplication des polynômes plutôt que de mémoriser une formule.
Une autre chose que vous devez garder à l’esprit est que les premier et deuxième termes n’ont pas besoin d’être composés d’un seul facteur. Chaque terme peut être composé de plusieurs facteurs, tels que :
Dans ce cas, soyez très prudent et n’oubliez pas d’élever tout le terme au carré, avec l’application de la propriété de la puissance correspondante.