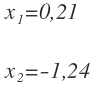En esta lección te explicaré cómo calcular la concavidad y convexidad de una función en un determinado intervalo sin necesidad de tener la gráfica de la función.
Pero antes, para no confundir términos, vamos a definir qué es una función cóncava y qué es una función convexa.
Si has llegado hasta aquí es porque necesitas un profesor de matemáticas online. Si después de leer esto, quieres que te ayude a entenderlas de verdad, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Concavidad y convexidad
Una función será cóncava en un intervalo cuando tenga esta «forma de valle»:
Una función será convexa en un intervalo cuando tenga «forma de montaña»:
No hay un criterio único para establecer si la concavidad y la convexidad se definen así o al contrario, por lo que es posible que en otros textos te lo encuentres definido al contrario.
Cómo saber si una función es cóncava o convexa en un intervalo
Teniendo en cuenta la definición anterior para concavidad y convexidad, una función será cóncava en un intervalo cuando el valor de la derivada segunda de un punto de ese intervalo sea mayor que cero:
Una función será convexa en un intervalo cuando el valor de la derivada segunda de un punto de ese intervalo sea menor que cero:
En los puntos de inflexión, la función cambia de cóncava a convexa o viceversa.
Ejercicio resuelto de cómo calcular la concavidad y convexidad en los intervalos de una función
Vamos a calcular los intervalos donde la siguiente función es cóncava o convexa:
Necesitamos estudiar el signo de la derivada segunda de la función. Por tanto, vamos a calcular la derivada segunda.
La derivada primera es:
Y la derivada segunda:
Ahora vamos a calcular en qué intervalos la derivada segunda es mayor o menor que cero.
Para ello, igualamos la derivada segunda a cero:
Y resolvemos la ecuación, cuyos resultados son:
Los colocamos en la recta numérica:
Tenemos 3 intervalos:
- Desde menos infinito hasta -1,24
- Desde -1,24 hasta 0,21
- Desde 0,21 hasta infinito
¿Cómo sabemos si f»(x) es positiva o negativa en cada intervalo?
Para cada intervalo, elegimos un punto que pertenezca a cada intervalo y calculamos el valor de f»(x) en ese punto.
Para el intervalo comprendido entre el menos infinito y el -1,24, elijo el punto x=-2. Calculo el valor de f»(-2):
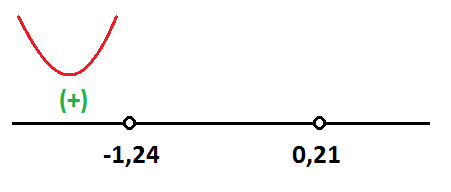
El resultado es mayor que cero, por lo tanto, la función será cóncava en el intervalo que va desde menos infinito hasta -1,24:
Y lo representamos así en la recta:
Seguimos con el intervalo que va desde -1,24 hasta 0,21. Elijo el punto x=0 y calculo el valor de f»(x) para ese punto:
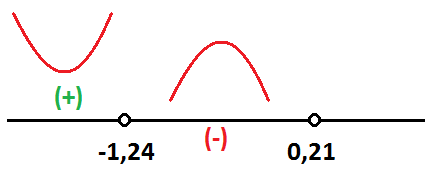
Es menor que cero, por lo que la función es convexa en ese intervalo:
Y lo representamos en la recta:
Para el tercer intervalo, elegimos el punto x=1:
La derivada segunda en ese intervalo es mayor que cero, por lo que la función será cóncava:
Cuya representación en la recta es:
Y ya tenemos los tres intervalos de la función definidos en cuanto a concavidad y convexidad se refiere.
¿Quieres aprender más sobre aplicaciones de las derivadas? Lo tienes en el Curso de Aplicaciones de las Derivadas. Con explicaciones paso a paso con todo detalle.
¿Necesitas clases de matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: