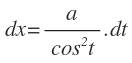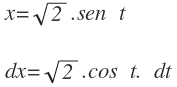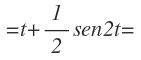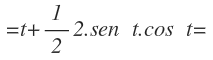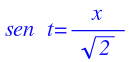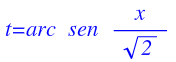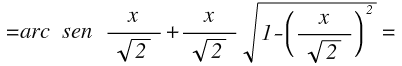A continuación te voy a explicar paso a paso cómo resolver la integrales irracionales mediante sustitución trigonométrica. Te lo explicaré paso a paso mientras resolvemos un ejemplo.
Si has llegado hasta aquí es porque necesitas un profesor de matemáticas online. Si después de leer esto, quieres que te ayude a entenderlas de verdad, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Te recomiendo que cojas papel y lápiz y la vayas resolviendo al mismo tiempo, ya que son muchos pasos y es muy fácil que te pierdas.
¡Vamos allá!
Sustituciones trigonométricas en integrales irracionales. Cambios de variable
Empezaré indicándote cuales son los cambios de variable a realizar en función del radical y de los términos que tengamos dentro.
A estos cambios de variable se le llaman sustituciones trigonométricas ya que se utilizan razones trigonométricas en las expresiones.
Tenemos tres casos:
Primer caso de sustitución trigonométrica
Cuando en la función a integrar aparece la raíz cuadrada de un número al cuadrado menos una variable x al cuadrado, es decir, de esta forma:
La sustitución trigonométrica que hay que hacer en este caso es igualar la variable x al número multiplicado por el seno de t:
Después derivamos en ambos miembros para obtener la equivalencia de dx en función de «t»:
Segundo caso de sustitución trigonométrica
Cuando en la función a integrar aparece la raíz cuadrada de un número al cuadrado más una variable x al cuadrado, es decir, de esta forma:
En este caso, la sustitución trigonométrica que hay que realizar es igualar la variable x al número multiplicado por la tangente de t:
Para hallar la equivalencia de dx en función de «t», derivamos en ambos miembros:
Tercer caso de sustitución trigonométrica
El tercer caso de sustitución trigonométrica es cuando en la función a integrar aparece la raíz cuadrada de variable x al cuadrado menos un número al cuadrado:
La sustitución trigonométrica a realizar es igualar x al número dividido entre el seno de t:
Derivamos en ambos miembros para obtener dx en función de «t»:
Existen otras formas de resolver integrales irracionales, las cuales las tienes explicadas en el Curso de Integrales.
Ejercicio resuelto de una integral irracional mediante sustitución trigonométrica
Vamos a resolver un ejemplo de una integral irracional en la que tengamos que realizar alguno de los cambios de variable propuestos en el apartado anterior.
Tenemos la siguiente integral:
Se trata de la integral de una función irracional, ya que tenemos un radical, pero no tenemos por qué saber cuál es el método de resolución o el cambio de variable a realizar. Antes hay que descartar otras posibilidades.
Si la integral hubiera sido de esta forma:
Se hubiera resuelto de una forma más simple, mediante integrales inmediatas, pero no tenemos el 2x y tampoco se lo podemos añadir, por lo que no podemos resolver la integral por este método.
Tampoco podemos resolver la integral por partes.
Así que, no queda más remedio que utilizar el método de integración con cambios de variable de sustituciones trigonométricas.
En este caso tenemos la raíz cuadrada de un número menos x al cuadrado. Si observamos los casos anteriores, la que más se le parece es el primer caso, pero para ello, necesitamos tener un número al cuadrado:
No tenemos ningún número elevado al cuadrado, por tanto, la primera clave para empezar a resolver la integral es retocarla, para que aparezca el primer término elevado al cuadrado y así podamos realizar el cambio de variable propuesto.
Como queremos que el número aparezca al cuadrado, el 2 lo podemos poner como raíz de 2 y elevarlo al cuadrado. De esta forma, sigue siendo 2 (no hemos variado el número) pero ya aparece elevado al cuadrado que es lo que estábamos buscando:
Ahora ya podemos realizar el cambio de variable, donde «a» es raíz de 2:
Sustituimos el nuevo valor de x y de dx en nuestra integral:
Ahora dentro de la raíz operamos y resolvemos los cuadrados:
Sacamos factor común al 2, dentro de la raíz:
Y sacamos el 2 fuera de la raíz, que pasa a multiplicar al raíz como raíz de 2:
Cambios trigonométricos para simplificar los cálculos
Llegados a este punto, tenemos que realizar varios cambios trigonométricos para simplificar los cálculos.
A partir del teorema fundamental de trigonometría, despejamos coseno de t:
Y si te das cuenta, es igual a uno de los radicales que tenemos. Por tanto, sustituimos ese radical por coseno de t. En este paso también he multiplicado las raíces de 2, cuyo resultado es 2 y sacado la constante fuera de la integral. Me ha quedado así:
Multiplicamos los dos cosenos que nos quedan dentro de la integral:
Y realizamos otro cambio trigonométrico, que nos hará la vida más fácil a la hora de integrar:
Lo sustituimos en nuestra integral:
Ahora separamos la fracción en una suma de dos fracciones (una por cada sumando del numerador y manteniendo el mismo denominador) y la integral de esa suma de fracciones la ponemos como una suma de integrales:
Sacamos las constantes fuera de cada integral:
Y por fin, integramos las dos integrales inmediatas que nos han quedado (bueno, la integral de coseno de 2t es casi inmediata):
Operamos para eliminar el paréntesis y nos queda:
Llegamos ahora a otro cambio trigonométrico, para simplificar el resultado, que es el siguiente:
Y lo sustituimos en nuestro resultado:
Y operamos las constantes:
Deshacer el cambio de variable
Ya no podemos simplificar más el resultado realizando cambios trigonométricos, ni operando con las constantes.
Por tanto, vamos a poner la solución en función de x, que es como debe darse el resultado, ya que el cambio de variable lo hemos hecho nosotros para poder integrar, pero el resultado hay que darlo siempre en función de x.
Para ello, debemos buscar una expresión en función de x, para cada uno de los términos en función de t, es decir, tenemos que poner t, seno de t y coseno de t, en función de x y eso lo vamos a ir obteniendo del cambio de variable que hicimos al principio.
Realizamos este cambio de variable:
De aquí podemos despejar seno de t, que lo tenemos en nuestra solución:
Ya tenemos una expresión de seno de t en función de x.
De esta última expresión, despejamos t y obtenemos su expersión en función de x
Nos queda encontrar la expresión para coseno de t. que la vamos a obtener del teorema fundamental:
Despejamos coseno de t y queda:
Como anteriormente hemos obtenido la expresión en función de x para el seno de t, la sustituimos en la expresión del coseno y queda:
Por lo que ya tenemos también la expresión en función de x del coseno de t.
Ahora sustituimos t, sen t y cos t en la solución y llegamos al fin a la solución de la integral irracional en función de x:
Hasta aquí ya está resuelta la integral, pero todavía podemos simplificar más el resultado.
Voy a seguir para que veas cómo se hace. Podemos resolver el cuadrado dentro de la raíz:
Dentro de la raíz realizamos la suma de fracciones:
Sacamos fuera de la raíz el denominador:
Ahora multiplicamos las fracciones que nos quedan en el segundo término y añadimos + C, porque no se puede simplificar más:
¡Por fin hemos terminado! 🙂
Como ves, para resolver integrales irracionales de este tipo, hay que tener en cuenta varios cambios trigonométricos. Lo bueno es que son siempre los mismos cambios (por eso te los he puesto en azul) y el procedimiento es siempre el mismo.
Si quieres aprender a integrar desde cero, o tienes dudas de como integrar y no sabes cómo resolverlas, te recomiendo el Curso de Integrales.
¿Necesitas clases de matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más:

Exámenes resueltos de Matemáticas II Selectividad (PBAU) Baleares

Exámenes resueltos de Matemáticas II Selectividad (EBAU) Canarias

Exámenes resueltos de Matemáticas II Selectividad (PevAU) Andalucía

Exámenes resueltos de Matemáticas II Selectividad (EvAU) Castilla-La Mancha

Exámenes resueltos de Matemáticas II Selectividad (EBAU) Extremadura

Exámenes resueltos de Matemáticas II Selectividad (EvAU) Navarra

Exámenes resueltos de Matemáticas II Selectividad (EAU) País Vasco