Vamos a ver una herramienta para resolver ejercicios de distribución binomial, que es aproximar la distribución binomial a la distribución normal. Veremos cómo ajustar una distribución binomial para poder resolverlo como si fuera una distribución normal, con ejercicios resueltos paso a paso.
Para entender esta explicación, es necesario que domines antes la distribución binomial, así como distribución normal, explicadas en el curso de estadística.
Por tanto, supondré que ya conoces los conceptos relacionados con ambas distribuciones.
¡Empezamos!
Si has llegado hasta aquí es porque quieres aprender cómo resolver algún ejercicio que no entiendes. ¿Has pensado en apuntarte a clases de matemáticas online?. Si después de leer esto, quieres que te ayude a entender las matemáticas de verdad, puedes hacer dos cosas: o seguir buscando por Internet o suscribirte e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Qué es aproximar la distribución binomial a la normal
Vamos a ver qué es aproximar la distribución binomial a la normal con un ejemplo:
Un jugador de baloncesto tiene un porcentaje de acierto del 65% en tiros libres. Realiza 100 lanzamientos. ¿Cuál es la probabilidad de que acierte 40?
Para calcular la probabilidad de que acierte 40 lanzamientos utilizamos la fórmula de distribución binomial:
En la que definimos X como encestar tiros libres:
La probabilidad de tener éxito, que es encestar el lanzamiento, es de 0,65:
La probabilidad de fracaso, que es fallar el lanzamiento, es:
Sustituimos las variables por sus valores en la fórmula:
Desarrollamos el número combinatorio, operamos en los exponentes, para finalmente llegar a la solución:
De la misma forma, puedo calcular la probabilidad de que acierte 24:
Y también puedo calcular la probabilidad de que acierte 62:
En realidad, puedo calcular la probabilidad de que acierte cualquier número de lanzamientos que esté entre 1 y 100, utilizando la fórmula distribución binomial.
Si calculara todas las probabilidades, es decir, la probabilidad de acertar 1 lanzamiento, la probabilidad de acertar 2 lanzamientos, la probabilidad de acertar 3 lanzamientos y así hasta la probabilidad de acertar 100 lanzamientos y las representara en unos ejes de coordenadas, donde en el eje horizontal tengamos el número de aciertos y en el eje vertical tengamos la probabilidad, nos quedaría algo como esto:
que si te das cuenta tiene forma de campana de Gauss, donde la línea roja corresponde a la distribución normal que se ajusta a esa distribución binomial, aunque el ajuste no es perfecto, ya que en la distribución binomial se toman valores discretos (sólo los valores enteros) y en la distribución normal, se toman valores continuos (cualquier valor), por lo que habrá que hacer una corrección de continuidad, que veremos cómo más adelante.
Por tanto, aproximar la distribución binomial a la normal, es utilizar la distribución normal que se ajusta a la representación de todas las probabilidades de la distribución binomial, para calcular las probabilidades.
¿Y qué probabilidades se calculan con la aproximación de la binomial a la normal? ¿Y cómo se calculan?
Es lo que veremos en el siguiente apartado.
Cómo calcular probabilidades con la aproximación de la binomial a la normal
En el apartado anterior hemos visto que podemos calcular la probabilidad de acertar cualquier número de lanzamientos utilizando la distribución binomial.
Pero, ¿qué pasa si me piden la probabilidad de encestar 60 lanzamientos o menos?
En ese caso, haciéndolo con la fórmula de distribución normal, tendría que ir calculando la probabilidad de encestar 1 hasta la probabilidad de acertar 60 y después sumarlos:
pero esto resulta poco práctico.
Por tanto, cuando tengamos un número muy grande de experimentos y tengamos que calcular la suma de muchas probabilidades conviene aproximar la distribución binomial a la distribución normal.
Para aproximar la distribución binomial a la normal, y trabajar con la curva normal obtenida hasta obtener la probabilidad pedida, tendremos que realizar estos tres pasos:
- Aproximar la distribución binomial B(n,p) a una distribución normal N(μ,σ)
- Realizar una corrección de continuidad
- Tipificar la distribución normal N(μ,σ) a una distribución normal estándar N(0,1)
Vamos a ver con detalle cada uno de estos pasos para resolver nuestro ejemplo
Aproximación de la binomial a la normal
Sabemos que una distribución binomial B(n,p) se puede aproximar a una distribución normal N(μ,σ)
Donde la media y la deviación típica de la distribución normal se calcular en función de los parámetros de la distribución binomial.
La media será igual:
Y la desviación típica:
donde:
- n = número de experimentos
- p = probabilidad de éxito
- q = probabilidad de fracaso
Siguiendo con el ejemplo anterior, vamos a calcular la probabilidad de encestar 40 lanzamientos o menos.
Recordamos que se realizan 100 lanzamientos y que la probabilidad de éxito es de un 65%, por lo que la distribución binomial es:
Vamos a calcular su aproximación a la normal.
La media es:
Y la desviación típica es:
Por lo que nos queda una distribución normal de media 65 y distribución normal 4,76:
Realización de una corrección de continuidad
Como hemos comentado antes, se puede obtener una curva de distribución normal que se ajusta a una distribución binomial, pero el ajuste no es perfecto, debido a que en la distribución binomial sólo se toman valores discretos, es decir, sólo se toman los valores enteros y en la distribución normal se puede tomar cualquier valor que esté dentro del intervalo de probabilidades que queremos calcular, es decir, tanto números enteros como números decimales.
Por tanto, para que el ajuste sea más preciso hay que hacer lo que se llama una corrección de continuidad, que es ampliar 0,5 unidades el intervalo de cálculo.
Pero cuidado, ampliar 0,5 unidades el intervalo de cálculo de probabilidad no significa sumar siempre 0,5, sino que se realiza de la siguiente forma:
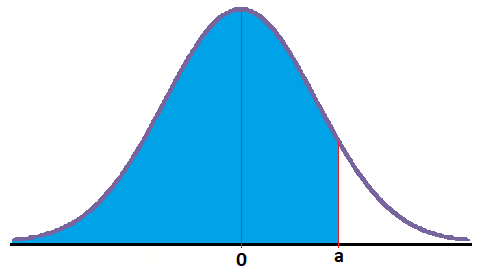
- Si el intervalo se encuentra a la izquierda de un límite superior, le sumamos 0,5 al límite superior
Esto se dará en los casos en los que busquemos que la probabilidad esté por debajo de un determinado valor:
- Si el intervalo se encuentra a la derecha de un límite inferior, le restamos 0,5 al límite inferior
Lo que se dará cuando calculemos que la probabilidad esté por encima de un determinado valor:
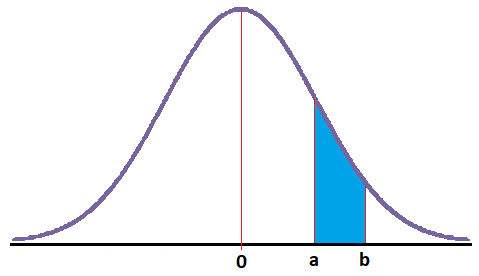
- Si el intervalo se encuentra entro dos límites, uno inferior y otro superior, le restamos 0,5 al límite inferior y le sumamos 0,5 al límite superior.
Que es lo que tendremos cuando queramos obtener la probabilidad entre dos valores:
Es decir, lo que buscamos siempre es que el área sombreada se amplíe y por tanto, la hacemos más grande sumando o restando 0,5 al límite superior o inferior según corresponda.
Siguiendo con el ejemplo, nos piden calcular la probabilidad de acertar 60 lanzamientos o menos:
Como tenemos un límite superior, para realizar la corrección de continuidad, le sumamos 0,5 al límite superior, por lo que para pode utilizar la aproximación a la curva normal, tenemos que calcular la probabilidad de ser menor o igual que 60,5:
Tipificación de la distribución normal a la distribución normal estándar
Lo que voy a realizar a continuación lo tienes explicado con detalle en las lecciones de tipificar la variable y la distribución normal estándar.
Una vez hemos aproximado la distribución binomial a la normal, que en nuestro caso es:
Vamos a tipificar la variable para poder utilizar las tablas de la distribución normal estándar N(0,1). Para ello, utilizamos la siguiente fórmula:
Sustituimos x, μ y σ por sus valores y obtenemos el valor de z:
Por tanto z=-0,94 de una distribución normal N(0,1) equivale a 60,5 de una distribución normal N(65, 4,76).
Así que ahora vamos a calcular la probabilidad de que z sea menor o igual a -0,94 en la distribución normal N(0,1):
Tal y como explico en la lección de la distribución normal estándar, la probabilidad de que z sea menor o igual que un número negativo es igual a la probabilidad de que z sea mayor que su valor en positivo, que a su vez es igual a 1 menos la probabilidad de que z sea menor o igual que el número en positivo:
El valor de P(z≤0,94) lo obtenemos de la tabla de distribución normal estándar, entrando por 0,9 en la primera columna y 0,04 en la primera fila:
Así que la probabilidad de que z sea menor o igual que -0,94 es:
Por tanto, la probabilidad de que enceste 60 lanzamientos o menos es 17,36%.
¿Necesitas ayuda en matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: