¿Qué es el dominio de una función?. ¿Cómo calcular el dominio de una función?
A continuación te explicaré paso a paso qué es el dominio de una función y te enseñaré cómo calcularlo.
Si has llegado hasta aquí es porque necesitas un profesor de matemáticas online o tal vez busques clases de matematicas. Si después de leer esto, quieres que te ayude a entenderlas de verdad, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Por si no lo sabes, una función se caracteriza porque a cada valor de x, le corresponde un único valor de f(x).
Sin embargo, hay veces para un determinado valor de x que no le corresponde ningún valor de f(x).
¿Y qué pasa cuando no le corresponde ningún valor de f(x)?
Pues que para ese valor de x, la función f(x) no existirá.
Vamos a ver cuando pueden ocurrir esos casos.
Cuándo una función no existe
Una función no existirá cuando para los valores de x que provoquen los siguientes casos:
1- Cuando un número quede dividido entre 0:
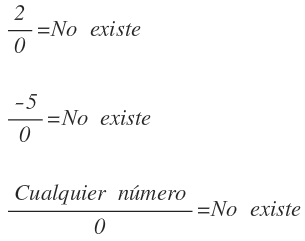
2- Cuando el contenido de una raíz de índice par es un número negativo

3- Cuando el contenido de un logaritmo es 0 o un número negativo

Ahora que ya sabes que una función puede tener un valor para unos valores de x o puede no existir para otros valores de x, voy a pasar a explicarte qué es el dominio de una función.
Qué es el dominio de una función
¿Qué es el dominio de una función?
Se designa como Dom f.
Visto así asusta un poco, pero conforme vayamos resolviendo ejemplos te va a ir quedando mucho más claro.
Para calcular el dominio de una función, debemos obtener los valores de x, para los que exista esa función. O dicho de otra forma, debemos encontrar para qué valores de x, la función no existe y quedarnos con los valores de x donde la función sí existe.
El dominio de una función depende mucho del tipo de función.
Vamos a verlo:
Cómo calcular el dominio de una función
Aquí tienes un vídeo con ejercicios resueltos sobre cómo calcular el dominio de una función:
Y si sigues leyendo tienes explicado lo que necesitas saber con todo detalle
Dominio de una función polinómica
Las funciones polinómicas son en las que no aparecen ni denominadores ni raíces.
La x puede aparecer sumando, restando, multiplicando o elevada a algún exponente, como por ejemplo:

En este tipo de funciones no existe ningún valor de x que haga que f(x) no exista. Por tanto, f(x) existe siempre.
Cuando una función existe siempre, su dominio es todo el conjunto de los números reales:

Cómo se calcula el dominio de una función racional
Las funciones racionales existen para todo R, menos para los valores que hacen 0 el denominador.
Por tanto, para calcular el dominio de una función racional, debemos encontrar los valores que hacen 0 el denominador y quitárselo a R.
Por ejemplo:

Esta función existirá siempre, menos cuando el denominador sea igual a 0. Por tanto, debemos encontrar esa restricción que anula al denominador.
Para que exista la función, el denominador debe ser distinto de 0:

Y esta restricción, es una ecuación de primer grado, de donde debemos despejar la x:

Cuando x=1, el denominador será 0. Por tanto, para que exista f(x), x tiene que ser distinto de 1 y ese es el valor que hay que quitarle a R:

El dominio es todo R menos el conjunto formado por el número 1.
Vamos a ver otro ejemplo:
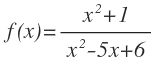
Igual que antes, esta función existirá siempre que el denominador no sea 0. Por tanto, calculamos los valores que hacen 0 el denominador:

Es decir, la función existirá siempre que x sea distinto de 2 y 3, por tanto el dominio es todo R menos 2 y 3:

Cómo se calcula el dominio de una función irracional
Las funciones irracionales son aquellas en las que aparece una raíz.
Las de índice impar existen siempre.
Las de índice par, existen siempre que su contenido sea igual o mayor que cero.
Por ejemplo:

Es una raíz de índice par, por tanto, existe siempre y cuando su contenido sea mayor o igual que 0:

De esta inecuación, despejamos x y nos queda:

Por tanto, la función existirá siempre y cuando x sea mayor o igual que -2. Su dominio es:

Otro ejemplo:

Es una raíz de índice impar, luego existe siempre y su dominio es todo R:

Cómo se calcula el dominio de una función logarítmica
Las funciones logarítmicas con aquellas que la x está dentro de un logaritmo.
Existen siempre y cuando el contenido del logaritmo no sea 0 o un número negativo, es decir, existirán siempre y cuando el contenido del logaritmo sea mayor que 0.
Por ejemplo:

Esta función existirá siempre que el contenido del logaritmo sea mayor que 0:

De esta desigualdad, despejamos la x y nos queda:
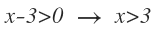
La función existirá siempre que x sea mayor que 3. Por tanto su dominio será:

Dominio de una función exponencial
Las funciones exponenciales son aquellas que tienen la x en el exponente, siendo la base:
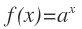
Donde «a» es un número real mayor que 0 y distinto de 1:

Podemos encontrarnos estas funciones como un número elevado a una función o también como el número e elevado a una función. Por ejemplo:
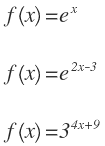
En las funciones exponenciales no existe ningún valor de x que haga que la función no exista. Por tanto, f(x) existe siempre.
El dominio de una función exponencial, es decir, un número elevado a una función o el número e elevado a una función, es todo el conjunto de los números reales:

¿Cómo identificar gráficamente el dominio de una función?
Gráficamente el dominio de una función son los valores de x para los que la gráfica de la función aparece dibujada encima. Si encima de un valor de x no hay nada, ese valor de x no pertenece al dominio.
El dominio entonces se mira siempre en el eje x.
Por ejemplo, tenemos la gráfica de la siguiente función, ¿cuál es su dominio?:

El dominio es el rango de valores de x, para los que está dibujada la función encima. Como vemos, desde 1 hasta 4, está dibujada la función. En ningún otro valor de x más:

Por tanto, el dominio de esta función será:
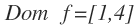
Por tanto, como ya hemos visto, el dominio de una función es el rango de valores para los cuales existe la función.
En el curso de funciones tienes explicado paso a paso cómo se calcula el dominio para funciones más complejas. También te explico cómo calcular el recorrido de una función, la composición de funciones. Te lo recomiendo.
Ejercicios propuestos
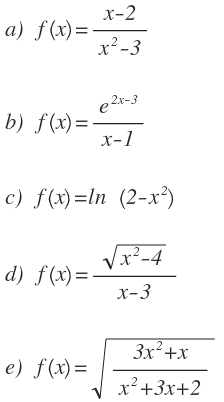
La solución de los ejercicios las tienes en el vídeo del principio 🙂
¿Necesitas ayuda en matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más:

Buah me a salvado esto agradecido a deu pai gracias por esto me a ayudado
Excelente y didáctica explicación, gracias.
Muy buena explicación
Muchas gracias, me ayudó con el examen 🙂
Muy buena la orientacion