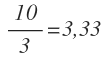A continuación voy a explicarte qué es esto de las reglas de divisibilidad, con ejercicios resueltos paso a paso. Vas a aprender a saber si un número es divisible entre otro sin necesidad de realizar la división.
Pero, ¿qué significa que un número sea divisible entre otro?
Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Te encuentras con el problema de que para saber si la división da exacta, tienes que hacerla. Sabes que existen unas criterios de divisibilidad, pero no sabes cómo se aplican.
Pruebas con el 2 al terminar la división, ves que no da exacta. Luego lo divides entre 3 y tampoco. Sigues con el 4 y así hasta que das con el 5 y entonces sí, has encontrado un número. Pero ya llevas un rato operando y te estás cansando.
Al dividir entre 5, el resultado es 109.317. Otro número alto, vuelta a empezar… lo dejas por imposible…
¿Te suena esta situación?
Pues aquí vas a aprender a utilizar las reglas de divisibilidad, o también llamadas criterios de divisibilidad.
Para empezar, ¿qué significa que un número es divisible por otro? Vamos a verlo
Que es la divisibilidad en matemáticas
En este vídeo te explico qué es la divisibilidad de un número:
Las ideas principales del vídeo son:
Se dice que un número es divisible por otro número cuando el resultado de su división es exacta, es decir, cuando su resto sea 0, o dicho de otra forma, cuando el resultado sea un número natural.
Que un número sea divisible entre otro es preguntarse: ¿se puede dividir entre este número? Y cuando se pregunta si se puede dividir, quiere decir si el resultado va a ser exacto.
Vamos a verlo con un ejemplo:
¿El 10 es divisible entre 2?
Entonces tenemos que preguntarnos, ¿el 10 se puede dividir entre 2?
Al hacer la división, vemos que su resultado es exacto. Es un número natural:
Por tanto, el 10 es divisible entre 2.
Otro ejemplo: ¿el 10 es divisible entre 3?
Nos volvemos a preguntar ¿el 10 se puede dividir entre 3?
El resultado no es exacto y por tanto el 10 no es divisible entre 3. (no se puede dividir entre 3)
¿Lo pillas? Ver si es divisible es comprobar si al dividir, el resultado es exacto.
Todos los números por los que se pueda dividir, son divisores de ese número.
Por definición, todos los números son divisibles como mínimo entre 1 y entre ellos mismos. Cuando no son divisibles entre ningún número más, estamos hablando de números primos.
Si además de poder dividirse entre 1 y entre ellos mismos, puede dividirse entre algún divisor más, que haga que el resto sea 0, entonces se trata de números compuestos.
Reglas de Divisibilidad. Ejemplos.
Vamos a ver qué son las reglas de divisibilidad y en concreto las reglas de divisibilidad del 2, del 3 y del 5:
Aquí tienes el contenido del vídeo:
Existen una serie reglas llamadas Reglas de Divisibilidad o Criterios de Divisibilidad que te permiten saber si un número es divisible por otro, sin necesidad de hacer la división, lo cual es muy útil sobre todo en números grandes.
Generalmente, estas reglas se utilizan para descomponer un número en factores primos.
Las más importantes son las reglas de los primeros números primos: 2, 3 y 5
En el Curso de Múltiplos y Divisores, tienes lecciones explicadas paso a paso lecciones sobre la descomposición de números en factores primos, así como el cálculo del m.c.m y del M.C.D. o ejercicios de múltiplos y divisores resueltos.
Regla de divisibilidad del 2
Para acordarte de esta regla, fíjate que el 2 también es un número par.
Vamos a ver un ejemplo de cómo aplicarla:
El número 26, ¿es divisible entre 2?
Sí, porque acaba en 6 y el 6 que es par.
El número 6548, ¿es divisible entre 2?
Sí, porque acaba en 8 y el 8 es par
El número 547, ¿se es divisible entre 2?
No, porque acaba en 7, que es impar
Y así siempre. Fácil ¿no?
Regla de divisibilidad del 3
Ésta puede ser la regla más complicada de las 3. Vamos a verla más despacio.
Para aplicarla hay que sumar las cifras del número y comprobar si la suma es múltiplo de 3. En caso afirmativo, será divisible entre 3.
El 12, ¿es divisible entre 3?
Tenemos que sumar sus cifras: 1+2 = 3
3 es múltiplo de 3, por tanto 12 es divisible entre 3
42, ¿es múltiplo de 3?
La suma de sus cifras es: 4+2 = 6
¿6 es múltiplo de 3? Sí, por tanto 42 es divisible entre 3
246, ¿es divisible entre 3?
La suma de sus cifras es: 2+4+6 = 12
12 es múltiplo de 3, luego 246 es divisible entre 3.
5465, ¿es divisible entre 3?
La suma de sus cifras es: 5+4+6+5 = 20
20 no es múltiplo de 3, luego 5465 no es divisible entre 3
Regla de divisibilidad del 5
Ésta regla también es muy fácil.
Vamos a ver unos pocos ejemplos:
5475 ¿es divisible entre 5?
Sí, porque acaba en 5
45780 ¿es divisible entre 5?
Sí, porque acaba en 0
34681 ¿es divisible entre 5?
No, porque no acaba en 0 ni en 5.
Un número puede ser divisibles entre más de un número. Por ejemplo el 30:
- Es divisible entre 2, porque acaba en 0
- Es divisible entre 3, porque la suma de sus cifras es 3, que es múltiplo de 3
- Es divisible entre 5, porque acaba en 0
Reglas de divisibilidad de otros números primos
En la práctica, se usarán las reglas de divisibilidad cuando tengas que descomponer un número en factores primos, que lo veremos en la siguiente lección.
Sabiendo las tres reglas anteriores, podrás descomponer la inmensa mayoría de los números.
Yo sinceramente no me sé ninguna otra.
Los criterios de divisibilidad de los demás factores primos no son nada prácticas, ya que se invierte menos tiempo en hacer la división que en aplicar la regla. Por tanto, yo recomiendo realizar la división directamente, ya que no hay que memorizar ninguna regla
Por ejemplo, la regla de divisibilidad del 7 es: Un número es divisible por 7 cuando la diferencia entre el número sin unidades y el doble de las unidades es 0 ó múltiplo de 7. En este caso, tardamos menos en dividir entre 7 y comprobar si es exacto o no.
Para terminar, recordarte que éstas reglas solo existen para los números primos. Es decir, no existe una regla de divisibilidad de 4 o de 6, ya que éstos números son compuestos.
Ejercicios sobre reglas de divisibilidad
1 – Indica si los números 24, 58, 61 y 586 son divisibles entre 2. Justifica tu respuesta
2 – Indica si los números 24, 336, 651 y 472 son divisibles entre 3. Justifica tu respuesta
3 – Indica si los números 35, 567, 720 y 100 son divisibles entre 5. Justifica tu respuesta
4 – Indica si los números 240, 654, 6571 y 16585 son divisibles entre 2, 3 y 5. Justifica tu respuesta
¿Necesitas ayuda en matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: