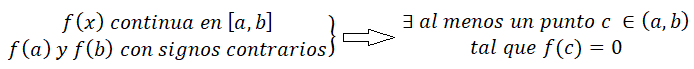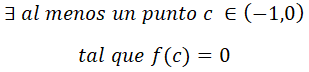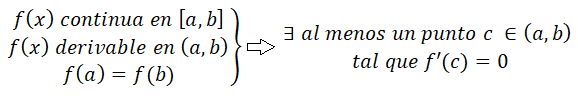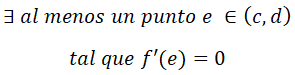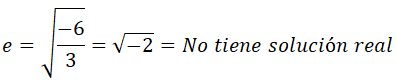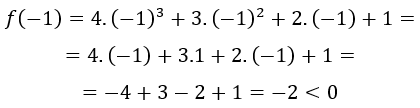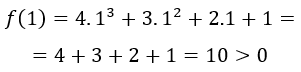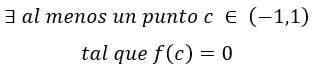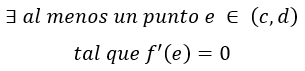A continuación te voy a explicar cómo demostrar que una función tienen una única raíz real en un intervalo, aplicando conjuntamente el teorema de Bolzano y el teorema de Rolle.
¡Empezamos!
Si has llegado hasta aquí es porque quieres aprender a resolver algún ejercicio. ¿Has pensado en apuntarte a clases de matemáticas online?. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Aplicación conjunta del teorema de Rolle y el teorema de Bolzano
Según el enunciado del teorema de Bolzano, si se cumplen las condiciones para el teorema se cumpla, existe como mínimo un punto c donde la función corta al eje x, pero puede existir más de uno.
Si queremos comprobar que la función corta una única vez al eje x en un intervalo, es decir, que sólo existe un punto c, ¿cómo lo tendríamos que hacer?
En este caso, tenemos que aplicar conjuntamente el teorema de Bolzano y el teorema de Rolle, para demostrar con el teorema de Bolzano, que la función corta al eje x y con el teorema de Rolle, que lo hace sólo una vez.
Vamos a ver esto más despacio resolviendo el siguiente ejercicio.
Comprobar que la siguiente función sólo puede tener una raíz real en el intervalo [-1,0]:
En primer lugar, con el teorema de Bolzano comprobaremos que existe al menos una raíz real, es decir, que al menos la función corta al eje x una vez.
Para ello, vamos a ir comprobando que cumple con las condiciones del teorema de Bolzano:
Al ser polinómica, la función siempre es continua, por lo que también es continua en el intervalo [-1,0]:
Ahora vamos a comprobar que el valor de la función tiene signos distintos en los extremos del intervalo.
Calculamos el valor de la función en x=-1:
En x=-1, la función es negativa.
Calculamos el valor de la función en x=0:
En x=0, la función es positiva.
Se cumplen las hipótesis del teorema de Bolzano, por lo que podemos afirmar que existe al menos un punto c perteneciente al intervalo (-1,0), donde la función es igual a cero:
Ahora vamos a demostrar con el teorema de Rolle, que la función sólo corta una vez al eje x, es decir, que sólo tiene una raíz real.
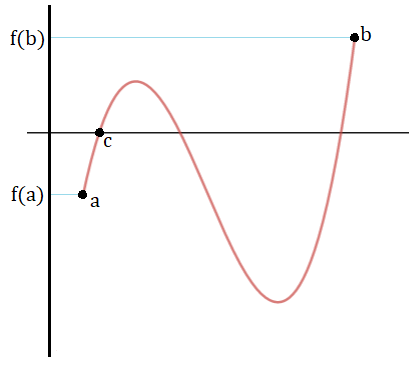
Supongamos que la función tiene esta forma (que no la tiene en la realidad):
Ya hemos comprobado que la función corta al eje x al menos una vez, que sería el punto c.
Suponemos que existe al menos otro punto, el punto d, perteneciente a (-1,0), donde la función también corta al eje x y por tanto f(d)=0:
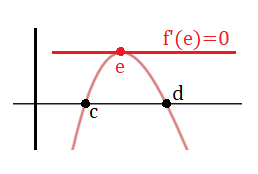
Según el teorema de Rolle, como f(c)=f(d), existiría un punto e, perteneciente al intervalo (c,d), donde su derivada es igual a cero, es decir, donde habría un máximo (o un mínimo):
Vamos a ver si esto es verdad, comprobando las hipótesis del teorema de Rolle:
Lo comprobaremos en el intervalo [c,d], que es donde la función tiene el mismo valor.
Al ser f(x) una función polinómica, es continua en todo R y por tanto también es continua en [c,d]:
Al ser f(x) una función polinómica, también es derivable en todo R y por tanto es derivable en (c,d):
Y como ya sabemos que f(c)=f(d)=0, se cumplen todas las condiciones del teorema de Rolle, por lo que existe al menos un punto e perteneciente al intervalo abierto (c,d), tal que f'(e)=0:
Vamos a calcular el punto e.
Obtenemos la derivada de la función:
La derivada en el punto e es igual a 0:
Sustituimos la x por e para obtener f'(e) y la igualamos a 0:
De esta ecuación de segundo grado despejamos e y nos queda:
La ecuación no tiene solución real, por lo que se está contradiciendo el teorema de Rolle y por tanto, no existe ningún punto d (ni ningún otro punto) donde la función corte al eje x, por lo que queda demostrado que la función sólo corta al eje x en el punto c, dentro del intervalo (-1,0), por lo que sólo tiene una raíz real.
Recuerda que era una suposición que existiera ese punto d. Como realmente no existe, por eso hemos llegado a una contradicción.
Ejercicios resueltos de los teorema de Rolle y Bolzano
Ejercicio 1
Probar que la siguiente ecuación tiene una única solución:
Para comprobar que esta ecuación tiene una única solución, debemos analizar la siguiente función:
Vamos a comprobar con el teorema de Bolzano, que la función corta al menos una vez el eje x.
Las condiciones del teorema de Bolzano son:
En este caso, no tenemos un intervalo de estudio, así que el primer paso es obtener ese intervarlo.
Para ello, tenemos que elegir al azar, un valor de x, para el que el valor de la función sea negativo y otro valor de x, para el que el valor de la función sea positivo.
Pruebo calculando el valor de la función con x=-1:
La función es negativa para x=-1
Ahora tengo que encontrar otro valor de x para el que la función sea positivo.
Pruebo calculando el valor de la función con x=1:
El valor de la función es positivo.
Por tanto, he encontrado un intervalo donde la función tiene signos contrarios que es:
Te recuerdo que hemos elegido estos valores al azar. Cualquier valor de x que haga el valor de la función positiva y negativa sería igualmente válido. Por ejemplo, el intervalo [-2,0] también es válido.
Ya sabemos que la función tiene signos distintos en los extremos del intervalo elegido [-1,1]. Ahora, seguimos comprobando que se cumplen las condiciones del teorema de Bolzano, viendo si es continua en ese intervalo.
Al ser polinómica, la función siempre es continua, por lo que también es continua en el intervalo [-1,1]:
Se cumplen las hipótesis del teorema de Bolzano, así que existe al menos un punto c perteneciente al intervalo (-1,1), donde la función es igual a cero:
Acabamos de demostrar con el teorema de Bolzano que existe como mínimo un punto c, donde la función corta al eje x, pero puede existir más de uno.
Para demostrar que la función sólo corta una vez al eje x y por tanto, la ecuación tiene una única solución, aplicaremos el teorma de Rolle.
Vamos a suponer que existe otro punto d, perteneciente a (-1,1), en el que la función también corta al eje x, por lo que f(d)=0:
Como los puntos c y d cortan al eje x, el valor de la función en esos puntos es iguala a cero y por tanto f(c)=f(d). Así que según el teorema de Rolle existiría un punto e, perteneciente al intervalo (c,d), donde su derivada es igual a cero, es decir, donde habría un máximo (o un mínimo):
Una vez que comprobemos que se cumplen las condiciones del teorema de Rolle en el intervalo [c,d], debemos comprobar si es posible calcular el punto e.
Si es posible, entonces existirá al menos otra solución, que será el punto d. Si no es posible, habremos llegado a una contradicción, porque no existe tal punto e y por tanto, habremos demostrado que la ecuación sólo tiene una solución.
Las hipótesis del teorema de Rolle son:
f(x) es una función polinómica, es continua en todo R y por tanto también es continua en [c,d]:
Como f(x) es una función polinómica, también es derivable en todo R y por tanto es derivable en (c,d):
Hemos partido de que f(c)=f(d)=0.
Se cumplen todas las condiciones del teorema de Rolle, por lo que existe al menos un punto e perteneciente al intervalo abierto (c,d), tal que f'(e)=0:
Vamos a ver si podemos calcular el punto e.
Obtenemos la derivada de la función:
La derivada en el punto e es igual a 0:
Sustituimos la x por e para obtener f'(e) y la igualamos a 0:
Resolvemos la ecuación de segundo grado:
La ecuación no tiene solución real, así que se está contradiciendo el teorema de Rolle. No existe ningún punto d donde la función corte al eje x.
Queda demostrado que la función sólo corta al eje x en el punto c, dentro del intervalo (-1,1), por lo que la ecuación sólo tiene una solución.
Hemos llegado a esta contradicción ya que el punto d era una suposición, pero realmente no existe.
¿Necesitas ayuda con las matemáticas? ¿Quieres que te explique cualquier duda que te surja paso a paso?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: