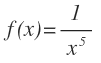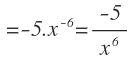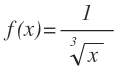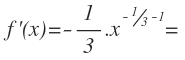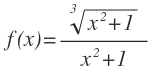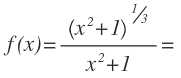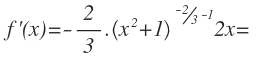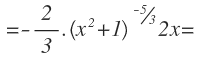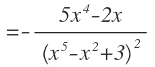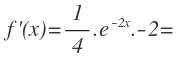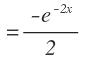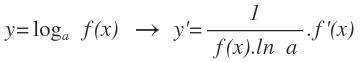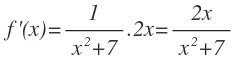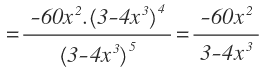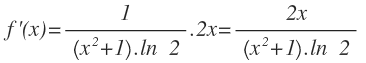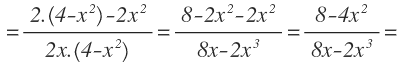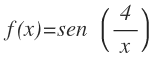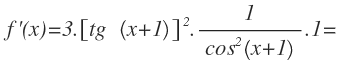A continuación te voy a explica cómo derivar funciones aplicando las fórmulas de las funciones derivadas y las reglas de derivación.
Te explicaré cómo derivar todos los tipos de funciones: funciones potenciales, funciones exponenciales, funciones logarítmicas y funciones trigonométricas, con ejercicios resueltos paso a paso, al mismo tiempo que te explico cuál es el procedimiento para resolverlas. Tienes muchas más explicaciones en el Curso de Derivadas.
Si has llegado hasta aquí es porque quieres aprender a resolver algún ejercicio. ¿Has pensado en apuntarte a clases de matemáticas online?. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Como derivar funciones potenciales
Vamos ver cómo derivar funciones potenciales, resolviendo unos cuantos ejercicios, en los cuales debemos sus correspondientes fórmulas:
Ejercicio 1
En este caso, aplicamos directamente la fórmula. El 6, que es el exponente pasa multiplicando y al exponente se le resta 1:
Y ya está derivada la función. Así de fácil.
Ejercicio 2
Para derivar esta función, debemos transformarla para que quede de la misma forma que en la fórmula, para ello, pasamos la potencia al numerador, cambiándole el signo al exponente:
Ahora procedemos igual que siempre: pasamos el exponente, con signo menos incluido, multiplicando y al exponente se le resta 1:
Después, operamos en el exponente y para mostrar la solución, pasamos el exponente como positivo volviendo a bajar la potencia al denominador:
Ejercicio 3
Este ejercicio es similar al anterior. Antes de aplicar la fórmula de la derivada de la función potencial, debemos transformar la función para que quede de la misma forma que en la fórmula.
Pasamos la raíz a su forma exponencial y subimos la potencia al numerador, cambiando de signo el exponente:
Para derivar, pasamos el exponente multiplicando, que en este caso es una fracción negativa y al exponente le restamos 1:
Operamos en el exponente, con mucho cuidado, ya que ahora tenemos una operación con fracciones, pasamos la potencia con exponente positivo, bajándola al denominador y cambiándole el signo al exponente y por último, volvemos a pasar la potencia de su forma exponencial a forma de raíz:
Ejercicio 4
Esta función se deriva aplicando la fórmula de la derivada de la función potencial compuesta, ya que tenemos una función elevada a un exponente.
Pasamos el exponente multiplicando a la función, al exponente le restamos 1 y multiplicamos todo por la derivada de la función que hay dentro del paréntesis:
Por último operamos en el exponente:
Ejercicio 5
Esta función no parece en un principio una función potencial y eso puede confundirte a la de derivarla.
Si te das cuenta, tenemos la misma función tanto en el numerador como en el denominador, por tanto, se puede considerar como un cociente de potencias de la misma base, donde la base es la función y por tanto, se puede mantener la base y restar sus exponentes.
Podemos poner la raíz en su forma exponencial:
Y ahora se ve mucho más claro, que tenemos la misma base, por lo que procedemos a restar sus exponentes:
Ahora ya se ve más claro que podemos derivarla utilizando la fórmula de la derivada de la función potencial.
Pasamos el exponente multiplicando, le restamos 1 al exponente y lo multiplicamos todo por la derivada de la función que queda dentro del paréntesis:
Ahora operamos en el exponente:
Y por último, simplificamos términos en el numerador, pasamos la potencia a exponente positivo y la volvemos a pasar a forma de raíz:
Ejercicio 6
Este ejercicio es similar al anterior, ya que en principio no parece una función potencial.
Podemos subir la función al denominador, cambiando de signo su exponente (que está elevada a 1):
Ahora ya podemos derivar siguiendo el mismo procedimiento que siempre:
Operamos en el exponente:
Y finalmente dejamos la potencia con exponente positivo:
Cómo derivar funciones exponenciales
Vamos a ver ahora unos ejercicios resueltos en lo que te explicaré cómo derivar funciones potenciales. Pondremos en práctica las siguientes funciones derivadas:
Ejercicio 1
Tenemos una función exponencial compuesta, es decir, un número elevado a una función, la cual es un cociente y se debe derivar mediante la derivada de una cociente:
Por tanto, aplicando directamente la fórmula de la función derivada de una función exponencial nos queda:
Para terminar, operamos en el numerador:
Ejercicio 2
En esta función, tenemos un número que multiplica a la función exponencial, o en otras palabras, un número que multiplica a una función.
Por tanto, lo primero que hay que aplicar es la fórmula de la derivada de una constante de una función:
donde para calcular la derivada, aplicamos la fórmula de la función exponencial:
Ejercicio 3
Tenemos una resta de funciones, donde los dos primeros términos son funciones exponenciales y además, el primer término es una función exponencial compuesta.
La derivada de esta función será la resta de las derivadas de cada uno de sus términos, en los que aplicaremos la fórmula de la función derivada de una función exponencial que corresponda en cada caso.
En el primer término aplicaremos la fórmula de la función exponencial compuesta, en el segundo, la derivada de la función e elevado a x es igual a e elevado a x y la derivada del tercer término es cero:
Ejercicio 4
Tenemos una multiplicación de funciones exponenciales.
Podríamos calcular su derivada aplicando la regla de la derivada de un producto:
Pero en este caso, vamos a resolverla tomando un camino mucho más sencillo que simplificará mucho los cálculos.
Como los dos factores están elevados al mismo denominador, puedo poner ambos entre paréntesis multiplicándose y elevados al exponente. Es lo contrario a tener una multiplicación elevada a una potencia, donde para resolver el paréntesis, se mantiene la base y se multiplican los exponentes (si lo necesitas puedes repasar las propiedades de las potencias). Después multiplico lo que me queda dentro del paréntesis:
Esto sólo puede hacerse porque ambos factores. Si no hubieran tenido el mismo exponente, no queda más remedio que aplicar la regla de la derivada de un producto.
Ahora sí, aplicamos la fórmula de la función derivada de una función exponencial compuesta:
Si quieres intentar resolverlo aplicando la regla de la derivada de un producto, al final tienes que aplicar propiedades de las potencias y los logaritmos y llegarás al mismo resultado.
Ejercicio 5
Esta función la puedes derivar aplicando la regla de la derivada de un cociente, o puedes considerar que la función exponencial está multiplicada por una constante, la cual es una fracción:
Aplicamos la fórmula de derivación de una constante por una función, cuya derivada es la derivada de una función exponencial compuesta:
Finalmente operamos y simplificamos:
Ejercicio 6
Tenemos una función elevada a un número, por lo que debemos aplicar la fórmula de la función derivada de una función potencial en primer lugar.
Después, para derivarla función exponencial de uno de los términos, aplicamos la fórmula de derivación de una función exponencial compuesta:
Por último, operamos:
Cómo derivar funciones logarítmicas
Con los siguientes ejercicios resueltos te explicaré el procedimiento para derivar funciones logarítmicas. Te recuerdo aquí las fórmula de las funciones derivadas de funciones logarítmicas que vamos a utilizar:
No sólo utilizaremos estas fórmulas, sino como verás, iremos aplicando las fórmulas de otros tipos de las funciones derivadas de otros tipos de funciones.
Ejercicio 1
Se trata de una función logarítmica compuesta. Aplicamos su correspondiente fórmula, donde para hallar f'(x) hay que aplicar la fórmula de la derivada de la función potencial:
Ejercicio 2
En este caso, la función que está dentro del logaritmo y de la que hay que obtener f'(x) es una función potencial compuesta, así después de aplicar la fórmula de la función derivada de una función logarítmica compuesta, aplicamos la de la derivada de una función potencial:
Después operamos por un lado en el denominador y por otro, para la función potencial, mantenemos la base y restamos los exponentes:
Ejercicio 3
Aplicamos directamente al fórmula de la función logarítmica de base a, donde en este caso es de base 2:
Ejercicio 4
Aplicamos la fórmula de la derivada logarítmica compuesta. Para hallar f'(x) tenemos que aplicar la regla de la derivada de un cociente:
Después operamos y simplificamos:
Como ves, las operaciones con polinomios empiezan a estar presentes, por lo que debes tener muy claro cómo operar con ellos. Si lo necesitas aprender más sobre las operaciones con polinomios, lo tienes explicado paso a paso en el Curso de Polinomios y en el Curso de Fracciones Algebraicas.
Ejercicio 5
Tenemos una función logarítmica compuesta, donde la función que está dentro del logaritmo vuelve a ser otro logaritmo. Por tanto, primero aplicamos la fórmula de la derivada compuesta de la función logarítmica y para hallar f'(x) utilizamos la de la derivada de la función logarítmica simple:
Ejercicio 6
Aplicamos la fórmula de la función derivada de una función logarítmica compuesta. Para obtener f'(x) utilizamos la regla de derivación del producto:
Obtenemos denominador común dentro del paréntesis:
Multiplicamos fracciones y simplificamos términos:
Por último, sacamos factor común al 2 en el numerador y en el denominador, para anularlos después y dejar el resultado completamente simplificado:
Cómo derivar funciones trigonométricas
Seguimos con ejercicios resueltos en los que te enseñaré a derivar funciones trigonométricas. Las fórmulas que necesitas las tienes en el Curso de Derivadas.
Ejercicio 1
Aplicamos directamente la fórmula de la función derivada compuesta del seno:
Ejercicio 2
En este caso tenemos una constante por una función trigonométrica. La constante la dejamos igual y la multiplicamos por la derivada, aplicando la fórmula de la derivada del seno:
También lo puedes resolver aplicando la regla de la derivada del producto.
Ejercicio 3
Tenemos una función trigonométrica compuesta. Para simplificar los cálculos, podemos considerar que la x está multiplicada por una constante:
Por tanto, derivamos aplicando la fórmula de la derivada del seno:
Ejercicio 4
Esta vez, después de aplicar la fórmula de la función compuesta del seno, no nos queda más remedio que calcular f'(x) con la regla de la derivada de un cociente:
Para terminar, operamos y queda:
Ejercicio 5
En este ejercicio, la función trigonométrica está elevada a 4, por tanto, para empezar a derivar tenemos que aplicar la fórmula de la función derivada de la función potencial compuesta, donde f'(x) corresponde a sen x, que lo derivamos con su fórmula correspondiente:
Ejercicio 6
Este es un caso similar al anterior, pero esta vez tenemos una función trigonométrica compuesta dentro del paréntesis, por tanto, primero aplicamos la fórmula de la derivada de la función potencial, después la de la derivada del coseno y por último la regla de la suma de las derivadas:
Por último, operamos:
Ejercicio 7
Tenemos una constante por una función. La función es una función trigonométrica compuesta por una función exponencial, por tanto, después de aplicar la fórmula de la derivada del coseno, aplicamos la fórmula de la derivada de la función exponencial para hallar f'(x):
Después reordenamos términos:
Ejercicio 8
Aplicamos directamente la fórmula de la derivada de tangente compuesta:
Ejercicio 9
Tenemos una función potencial, donde la función de dentro del paréntesis es una función trigonométrica, que a su vez es compuesta por una función polinómica.
Por tanto, primero aplicamos la fórmula de la derivada de la función potencial compuesta, donde para calcular f'(x) aplicamos la fórmula de la derivada de la tangente compuesta, que a su vez calculamos f'(x) con la regla de la suma de las derivadas:
Por último operamos y reordenamos términos:
Ejercicio 10
Tenemos la función trigonométrica de la tangente compuesta por otra función trigonométrica, la del seno.
Aplicamos primero la fórmula de la derivada de la tangente compuesta y hallamos f'(x) aplicando la fórmula de la derivada del seno, quedando:
No hay un único camino para derivar una función. Utiliza siempre el que simplifique los cálculos o con el que te sientas más cómodo sabiendo que estás haciendo las cosas bien.
Si quieres aprender a derivar desde cero, te recomiendo el Curso de Derivadas, en el que te explico desde el principio cómo aprender a derivar. Con ejercicios resueltos paso a paso y propuestos para practicar.
¿Necesitas ayuda con las matemáticas? ¿Quieres que te explique cualquier duda que te surja paso a paso?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: