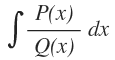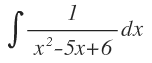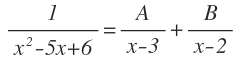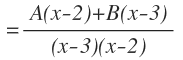¿Sabes cómo integrar funciones racionales? ¿Sabes identificar qué método de integración utilizar?
No sólo es importante saber cómo integrar funciones racionales realizando el método de integración correctamente, sino que todavía es más importante saber qué método de integración hay que aplicar.
Uno de tus problemas puede ser que cuando ves una integral, no sabes qué método de integración utilizar, aunque sepas aplicar el método.
Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
A continuación voy a explicarte no solo cómo integrar funciones racionales, sino a saber cuándo hay que aplicar estos métodos, o mejor dicho, cuando no hay que aplicarlos. Pero vamos a empezar por el principio:
¿Qué es una función racional?
Una función racional es aquella que tiene forma de fracción, cuyo numerador y denominador son polinomios. Tienen esta forma:
Estos son algunos ejemplos de funciones racionales:
El grado del polinomio del numerador P(x), puede ser cero, como por ejemplo:
Sin embargo, el grado mínimo del polinomio del denominador Q(x) debe ser mayor o igual a 1, ya que si fuera cero, no tendríamos ninguna fracción, sino un polinomio:
Una vez dicho esto, voy a explicarte cómo integrar funciones racionales en el siguiente apartado.
Cómo integrar funciones racionales paso a paso
Para saber cómo integrar funciones racionales debemos prestar atención a los grados del numerador y del denominador. Si tenemos esta integral:
Podemos distinguir dos grupos:
1 – Que el grado del polinomio del numerador sea menor que el grado del polinomio del denominador
Y dentro de este grupo tenemos tres casos:
1.1 – Q(x) tiene raíces reales distintas
1.2 – Q(x) tiene raíces reales múltiples
1.3 – Q(x) tiene raíces complejas
Si no tienes muy claro qué son las raíces de un polinomio, lo tienes explicado detalladamente en el Curso de Polinomios. Te lo recomiendo si quieres dominar las operaciones con polinomios
El otro grupo que podemos distinguir entre las integrales de funciones racionales es:
2 – Que el grado del polinomio del numerador sea mayor o igual que el grado del polinomio del denominador
Dependiendo qué tipo sea, se aplicará un método u otro.
Ahora voy a centrarme en explicarte cómo integrar funciones racionales que están en el primer grupo (grado P(x) < grado Q(x)) y dentro de ellas las que tengan raíces reales distintas.
Para aprender cómo integrar los demás tipos de funciones racionales, te recomiendo el Curso de Integrales Indefinidas, con el que aprenderás a integrar paso a paso desde el principio.
Vamos a explicarlo con un ejemplo, paso por paso.
Cómo resolver integrales racionales con raíces simples distintas en el denominador
Como te he comentado antes, voy a realizar un ejemplo cuando el polinomio del denominador tiene raíces reales distintas.
Por ejemplo, tenemos esta integral:
¿Cómo sé qué método de integración utilizar? El primer paso consiste en identificar qué tipo de integral se trata.
Tenemos que ir descartando métodos de integración. No puede resolverse con ninguna integral inmediata de una función simple, ya que en el denominador tenemos una función con más de un término.
La integral inmediata de una función compuesta que más puede parecerse es la de tipo logarítmico:
Pero si intentamos resolverla con esta integral inmediata, debemos realizar el siguiente cambio de variable:
Y no tenemos términos para sustituir dt, ni tampoco los podemos añadir.
Hubiera sido posible aplicar esta integral inmediata si hubiéramos tenido que integrar esta función:
Que si te das cuenta, también es la integral de una función racional, pero se resuelve con el método de la integral inmediata de una función compuesta.
Si no tienes claro cómo integrar utilizando el cambio de variable, en el Curso de Integrales Indefinidas lo tienes explicado paso a paso.
Por tanto, una vez descartados los otros métodos de integración es cuando aplicamos el método que te voy a enseñar. Tenemos por tanto la integral de una función racional:
De la forma:
Donde el grado del polinomio del denominador es mayor que el grado del polinomio del numerador:
Para poder integrar esta fracción, tenemos que descomponerla en una suma de fracciones simples, en las que el grado del numerador será 0, es decir, tendremos un número y el grado del denominador será 1, con el fin de que cada una de esas fracciones simples se puedan integrar después con integrales inmediatas de tipo logarítmico:
Vamos a proceder a descomponer la fracción en una suma de fracciones simples:
En primer lugar, tenemos que factorizar el polinomio del denominador.
En este caso es un polinomio de grado 2. Para descomponerlo hallamos sus raíces (soluciones de la ecuación de segundo grado) y para ello lo igualamos a 0 y resolvemos la ecuación:
Cuyas soluciones son:
En este punto es donde sabemos que el denominador tiene raíces reales distintas.
Cada raíz del polinomio puede escribirse de forma de binomio (x-a), donde a es el valor de cada raíz y además, un polinomio cualquiera puede escribirse como el producto de todos sus binomios (x-a). Por tanto:
Si el polinomio del denominador fuera de grado 3 o superior habría que utilizar otros métodos para descomponerlo. Tienes todos los métodos de descomposición de polinomios explicados paso a paso en el Curso de Polinomios
Ahora, la fracción de la integral, puede escribirse como una suma de fracciones cuyos denominadores son cada uno de los factores del denominador:
Y los numeradores de cada fracción son dos constantes que no conocemos:
Ahora vamos a calcular el valor de A y B.
Tenemos una suma de dos fracciones con distinto denominador. Para poder sumarlas hay que hallar denominador común, que será la multiplicación de los denominadores:
Y para hallar cada nuevo numerador, se divide el denominador común entre el denominador de cada fracción inicial y el resultado se multiplica por el numerador de la fracción inicial:
Y esto lo podemos escribir como una sola fracción:
Y al llegar aquí hemos llegado a la siguiente conclusión: La fracción original es igual a la fracción que acabamos de calcular:
Por tanto, como sabemos que los denominadores son iguales:
Los numeradores también serán iguales:
Y nos quedamos con esta última expresión. Le vamos a dar valores a la x para calcular A y B.
Los valores que hay que darle son las raíces del polinomio, ya que hará que se anule A o B y sepamos su resultado. Entonces:
Ahora que sabemos los valores de A y B, los sustituimos en esta expresión que teníamos al principio:
Y ya tenemos descompuesta la fracción en una suma de fracciones simples. Para entender lo que hemos hecho hasta ahora, es necesario que domines cómo operar con polinomios y con fracciones algebraicas.
Si te suscribes como alumno premium, te lo puedo explicar más despacio, al mismo tiempo que me preguntas otras dudas. O también puedes estudiarlo más despacio con el Curso de Polinomios
Seguimos con la integral. Ahora, escribimos la integral con nuestras nuevas fracciones simples:
Y cada una de estas integrales son integrales inmediatas de tipo logarítmico:
Que las resolvemos y añadimos la constante:
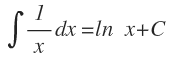
¿Dominas las integrales inmediatas? Es otra de las cosas que necesitas dominar y que también te puedo explicar paso a paso.
¿Necesitas ayuda con las matemáticas? ¿Quieres que te explique paso a paso cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más:
Exámenes resueltos de Matemáticas II Selectividad (PAU) Valencia
Exámenes resueltos de Matemáticas II Selectividad (EBAU) Canarias
Exámenes resueltos de Matemáticas II Selectividad (EBAU) Murcia
Exámenes resueltos de Matemáticas II Selectividad (EBAU) La Rioja
Exámenes resueltos de Matemáticas II Selectividad (EBAU) Asturias
Exámenes resueltos de Matemáticas II Selectividad (EvAU) Navarra
Exámenes resueltos de Matemáticas II Selectividad (EBAU) Extremadura