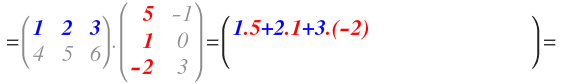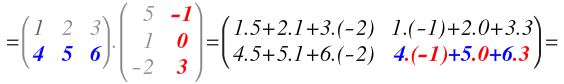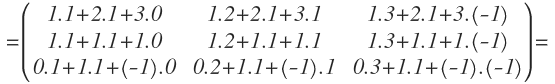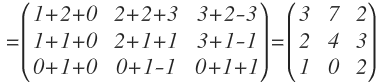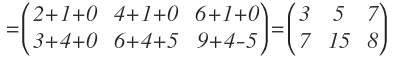¿Quieres aprender la multiplicación de matrices paso a paso? A continuación te voy a explicar cómo se hace el producto de matrices, con ejercicios resueltos paso a paso.
Al contrario que ocurre con los números, que podemos multiplicar cualquiera de ellos, no podemos multiplicar cualquier matriz.
Si has llegado hasta aquí es porque quieres aprender a resolver algún ejercicio. ¿Has pensado en apuntarte a clases de matemáticas online?. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Cómo multiplicar matrices. Producto de matrices
Para multiplicar dos matrices, se debe cumplir una condición muy importante:
Para definir las dimensiones de una matriz, 2×2, 3×3, 3×2… la primera dimensión hace referencia a las filas de la matriz y la segunda dimensión a las columnas:
Por tanto, si tenemos una matriz A de m filas y n columnas, sólo la podremos multiplicar por una matriz B que tenga n filas y p columnas (mismo número de columnas de A, que de filas de B):
La matriz resultante tendrá el mismo número de filas que A y el mismo número de columnas que B.
De todas formas, no tienes que aprenderte esto de memoria para saber cómo multiplicar matrices. Sólo tienes que quedarte con que no se pueden multiplicar cualquier matriz. Siempre deben cumplir la condición anterior y que la matriz resultante, tendrá unas dimensiones distintas a las dos matrices que se multiplican.
Producto de matrices. Ejercicios resueltos
Aquí tienes un vídeo con ejercicios resueltos paso a paso de la multiplicación de matrices:
Y si sigues leyendo tienes explicado los pasos más despacio.
Vamos a ver cómo se realiza el producto de matrices con uno ejercicios.
Ejercicio 1
Sean las matrices A y B las siguientes:
Multiplicar AxB.
En primer lugar, ¿pueden multiplicarse AxB?
Nos tenemos que fijar en las columnas de A y en las filas de B. La matriz A tiene 3 columnas y la matriz B tiene 3 filas. Son iguales y por tanto se pueden multiplicar.
Para multiplicar dos matrices, debemos multiplicar cada fila de la primera matriz, por cada columna de la segunda matriz.
Vamos a verlo paso a paso.
En primer lugar multiplicamos la primera fila de A, por la primera columna de B. Se realiza un producto escalar, es decir, se van multiplicando los elementos de la fila y de la columna y sus resultados se van sumando de la siguiente forma:
El primer elemento de la fila por el primer elemento de la columna…
…más…
el segundo elemento de la fila por el segundo elemento de la columna…
…más…
…el tercer elemento de la fila por el tercer elemento de la columna.
Esta operación, que es el resultado de multiplicar la primera fila por la primera columna, formará primer elemento de la primera fila de la matriz resultante:
Seguimos multiplicando la primera fila de A por la segunda columna de B. Volvemos a multiplicar cada elemento de la fila, por cada elemento de la columna (primero por primero, segundo por segundo y tercero por tercero) y la operación formará el segundo elemento de la primera fila de la matriz resultante:
Hasta ahora hemos multiplicado la primera fila de A por todas las columnas de B. Con sus resultados, hemos formado la primera fila de la matriz resultante.
Repetimos lo mismo con la segunda fila de A, multiplicándola por cada una de las columnas de B.
Seguimos con la segunda fila de A por la primera columna de B, cuyo resultado formará el primer elemento de la segunda fila:
Y para terminar multiplicamos la segunda fila de A por la segunda columna de B, para formar el segundo elemento de la segunda fila:
Ahora ya hemos multiplicado todas las filas de A por todas las columnas de B y sólo queda realizar las operaciones que nos quedan en cada elemento:
Date cuenta que las dimensiones de la matriz resultante son distintas de A y de B (tiene las mismas filas que A y las mismas columnas de B).
Ejercicio 2
Calcula los productos posibles entre las siguientes matrices:
Lo que nos piden en este ejercicio es multiplicar las matrices que se puedan multiplicar. Para ello, el número de columnas de la primera matriz debe ser igual al número de filas de la segunda matriz.
Vamos a empezar con la matriz A que tiene 3 columnas. Esta matriz la podremos multiplicar por las matrices que tengan 3 filas. En primer lugar, la podemos multiplicar por la misma matriz A, que también tiene 3 filas.
Realizamos el producto de matrices de A.A=
Multiplicamos filas por columnas:
Y operamos:
La matriz B también tiene 3 filas, por lo que podemos realizar la multiplicación de A.B=
Multiplicamos filas por columnas y operamos:
Seguimos con la matriz B que tiene 1 columna. La podemos multiplicar por cualquier matriz que tenga 1 fila, pero en este caso no tenemos ninguna, ya que la matriz A tiene 3 filas, la propia matriz B tiene 3 filas y la matriz C tiene 2 filas. Por tanto, la matriz B no la podemos multiplicar por ninguna matriz.
Por último vamos a ver los posibles productos de matrices con la matiz C. La matriz C tiene 3 columnas, por lo que la podemos multiplicar por matrices que tengan 3 filas.
La matriz A tiene 3 filas, por lo multiplicamos C.A:
Multiplicamos filas por columnas:
Y operamos:
La matriz C también se puede multiplicar por la matriz B, que tiene 3 filas:
Multiplicamos filas por columnas y operamos:
Ahora que ya sabes cómo multiplicar matrices, vamos a ver las propiedades del producto de matrices cuadradas.
Propiedades de la multiplicación de matrices cuadradas
1- El producto de matrices cuadradas cumple la propiedad asociativa
2- El elemento neutro es la matriz identidad
Cualquier matriz multiplicada por la matriz identidad dará como resultado la misma matriz. La matriz identidad es como si fuera el 1 para los números.
3- La multiplicación de matrices no es conmutativa en general.
Por norma general, la multiplicación de A por B no tiene el mismo resultado que B por A
Puede existir el caso de que A.B=B.A, pero no es lo normal.
4- Es distributiva respecto de la suma
5- El producto de dos matrices no nulas puede ser una matriz nula.
Por ejemplo:
6- Dada una matriz cuadrada A, no siempre existirá una matriz inversa que cumpla:
Ejercicios propuestos de multiplicación de matrices
Ejercicio 1
Dadas las matrices A y B:
Calcula el valor de a y b para que se cumpla que A²=A-B
En primer lugar calculamos la matriz A² multiplicando A por A:
Ahora calculamos A-B:
Igualamos ambas expresiones:
Para que ambas matrices sean iguales, todos los elementos de la matriz del primer miembro tienen que ser iguales que todos los elementos de la matriz del segundo miembro.
Vemos que todos los elementos de ambas matrices son iguales a excepción del segundo y tercer elemento de la primera columna de cada matriz, así que para que sean iguales, debemos igualar esos elementos de cada matriz.
Por tanto, igualamos los segundos elementos de la primera columna de ambas matrices:
De donde podemos despejar «a»:
De la misma forma, igualamos los terceros elementos de la primera columna de ambas matrices:
Sustituimos «a» por su valor:
Y despejamos el valor de b:
¿Te ha quedado claro cómo multiplicar matrices? ¿Tienes alguna duda más sobre matrices? En el Curso de Matrices te enseño paso a paso todo lo que necesitas saber: cómo calcular al inversa de una matriz, cómo resolver sistemas de ecuaciones, todas las operaciones con matrices… Con ejemplos y ejercicios resueltos
¿Necesitas ayuda en matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más:
Exámenes resueltos de Matemáticas II Selectividad (EvAU) Castilla-La Mancha
Exámenes resueltos de Matemáticas II Selectividad (EBAU) Extremadura
Exámenes resueltos de Matemáticas II Selectividad (EBAU) La Rioja
Exámenes resueltos de Matemáticas II Selectividad (EvAU) Navarra
Exámenes resueltos de Matemáticas II Selectividad (EAU) País Vasco
Exámenes resueltos de Matemáticas II Selectividad (EvAU) Madrid
Exámenes resueltos de Matemáticas II Selectividad (EBAU) Murcia