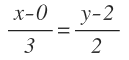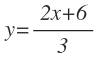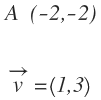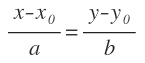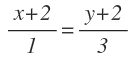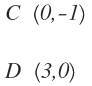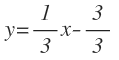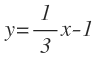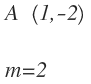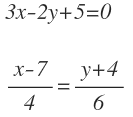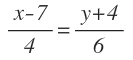A continuación vamos a resolver paso a paso varios ejercicios sobre el cálculo de la ecuación de una recta en diferentes tipos de escenarios, jugando con las diferentes formas de la ecuación de la recta hasta llegar a la solución.
Estos ejercicios se pueden resolver de varias formas. No existe una única forma de resolverlos.
Para entenderlo todo, debes dominar todas las formas que te puedes encontrar la ecuación de una recta, lo cual lo tienes explicado en el Curso de Geometría Analítica en el Plano.
Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Ecuaciones de la recta. Ejercicios
Ejercicio 1
Dada la recta de ecuación 2x-3y+6=0, escríbela en forma contínua, paramétrica, vectorial y explícita.
Tenemos la siguiente recta:
De donde podemos obtener el vector de dirección y un punto que pertenece a la recta. Con estos dos datos, podemos obtener la ecuación vectorial, la paramétrica y la contínua.
El vector de dirección es:
Para obtener un punto de la recta, le damos a x el valor que queramos, por ejemplo x=0 y despejamos el valor de «y»:
Por lo que el punto que pertenece a la recta es:
Con este punto y el vector de dirección obtenemos la ecuación vectorial:
Y la ecuación contínua:
La ecuación explícita la vamos a obtener a partir de la ecuación contínua.
Pasamos el 3 multiplicando al segundo miembro y el 2 multiplicando al primer miembro:
Operamos para eliminar paréntesis:
Y despejamos «y»:
Finalmente, separamos la fracción en dos términos para que se quede en forma explícita:
Esta ecuación también la podemos obtener a partir de la ecuación general:
Despejando la «y» y separando después en dos términos como acabamos de hacer.
Ejercicio 2
El punto P (3,1), ¿pertenece a la recta que pasa por el punto A (-2,-2) y tiene como vector director v=(1,3)?
Para saber si el punto pertenece a la recta, vamos a calcular la ecuación contínua y después sustituiremos las coordenadas del punto por la x y por la «y» en la recta y veremos si se cumple al igualdad.
Entonces, tenemos el punto y el vector de dirección:
En la ecuación contínua:
Sustituimos X0 e Y0 por las coordenadas del punto, y a y b por las coordenadas del vector de dirección:
Operamos para eliminar los paréntesis de los numeradores:
Ya tenemos la ecuación contínua.
Ahora, vamos a ver si el punto P (3,1) pertenece a esa recta:
Sustituimos sus coordenadas por x y por «y»:
Operamos en ambos miembros y vemos que no se cumple la igualdad:
Por tanto, el punto P (3,1) no pertenece a la recta
Ejercicio 3
Determina la ecuación de las rectas siguientes y expresa en forma implícita y explicita:
a: la recta que corta los ejes de coordenadas en los puntos C(0,-1) D(3,0)
b: la recta que pasa por el punto A(1,-2) y tiene pendiente m=-2
c: la recta que pasa por el punto A(1,-2) y forma un angulo de 135º con el sentido positivo del eje de las abcisas.
a: la recta que corta los ejes de coordenadas en los puntos C(0,-1) D(3,0)
Tenemos los puntos:
Calcularemos la ecuación de la recta por medio de la ecuación que pasa por dos puntos:
Sustuímos X1 e Y1 por las coordenadas el punto C y X2 e Y2 por las coordenadas del punto D:
Operamos y queda:
Pasamos el 3 multiplicando al segundo miembro:
Operamos para eliminar el paréntesis:
Para obtener la ecuación implícita pasamos todos los términos al primer miembro y reordenamos:
Para obtener la ecuación explícita, despejamos la «y»:
Y separamos en dos términos, uno con x y otro sin x:
Y simplificamos el segundo término:
b: la recta que pasa por el punto A(1,-2) y tiene pendiente m=-2
Tenemos un punto y la pendiente:
Calcularemos la ecuación de la recta con la ecuación punto pendiente:
Sustituimos X0 e Y0 por las coordenadas del punto y m por su valor:
Operamos:
La ecuación implícita la obtenemos pasando todos los términos al primer miembro y reordenando:
Y la ecuación explícita despejando «y»:
c: la recta que pasa por el punto A(1,-2) y forma un angulo de 135º con el sentido positivo del eje de las abcisas.
Operamos:
La ecuación implícita la obtenemos pasando todos los términos al primer miembro y reordenando:
Y la ecuación explícita despejando «y»:
c: la recta que pasa por el punto A(1,-2) y forma un angulo de 135º con el sentido positivo del eje de las abcisas.
Tenemos un punto y e ángulo que forma con el eje positivo de las x:
A partir del valor del ángulo, calculamos la pendiente:
Y con este valor de la pendiente y el punto A, calculamos la ecuación de la recta mediante la ecuación punto pendiente:
Sustituimos en la fórmula las coordenadas del punto y el valor de la pendiente:
Operamos:
La ecuación implícita será:
Y la ecuación implícita:
Ejercicio 4
Determina las ecuación explícita de una recta que pasa por el origen de coordenadas y es paralela a la recta que pasa por los puntos A(-2,5) B(3,-1).
En primer lugar calcularemos la pendiente que pasa por los puntos:
Mediante esta fórmula:
Sustuímos X1 e Y1 por las coordenadas el punto A y X2 e Y2 por las coordenadas del punto B y operamos:
Ya tenemos el valor de m.
Como la recta que vamos a calcular es paralela a esa, el valor de m es el mismo, por tanto, calcularemos la ecuación de la recta con ese valor de m y el punto:
Lo hacemos mediante la ecuación punto pendiente:
Sustituimos las coordenadas del punto y de la pendiente por sus valores:
Y operamos, llegando a su ecuación explícita:
Ejercicio 5
Las rectas 3x-2y+4=0 y ax-2y+3=0 son paralelas. Calcula a.
Tenemos estas dos rectas:
Y el enunciado nos dice que son paralelas, por lo que su pendiente es la misma. Por tanto, vamos a obtener la pendiente de cada una de las rectas, para igualarlas y obtener así el valor de a.
Para obtener su pendiente, ponemos las rectas en su forma explícita y el valor que quede multiplicando a la x será la pendiente:
En la primera recta:
Despejamos «y»:
Separamos el segundo miembro en dos términos:
Y simplificamos:
La pendiente de esta recta es:
Para la segunda recta hacemos lo mismo:
Despejamos «y»:
Y separamos el segundo miembro en dos términos, uno con x y otro sin x:
La pendiente en este caso es lo que queda multiplicando a la x que es:
Una vez tenemos las dos pendientes de las rectas, las igualamos y de ahí despejamos el valor de a:
Por tanto, a=3 para que la rectas sean paralelas.
Ejercicio 6
Adivina si las rectas 3x-2y+5=0 y x-7/4 = y+4/6 son paralelas o se cortan. Si son paralelas, indica el factor de proporcionalidad de sus vectores directores y, si son incidentes, calcula el punto de intersección.
Este ejercicio es similar al anterior. Para saber si las dos rectas son paralelas tenemos que obtener la pendiente de cada una de ellas y ver si son iguales. Para ello, las pondremos en su forma explícita y veremos qué número queda multiplicando a la x.
Tenemos las rectas:
La primera recta está en forma implícita:
Vamos a ponerla en forma explícita.
Para ello despejamos «y»:
Y separamos el segundo término en dos miembros:
La pendiente para esta recta es:
La segunda recta está en forma contínua:
Para pasarla a forma explícita, primero pasamos los denominadores multiplicando al otro miembro:
Operamos para eliminar los paréntesis:
Despejamos y:
Separamos el segundo término en dos miembros:
Y simplificamos:
La pendiente de esta recta es:
Las dos pendientes son iguales, por lo que las rectas son paralelas y no se cortan.
Ejercicio 7
Calcula la ecuación explicita de la recta que pasa por el punto A (4,3) y es perpendicular a la recta: 3x+y-5=0.
Tenemos el punto A y la recta:
Necesitamos calcular la pendiente de la nueva recta, que la calcularemos a partir de la recta que nos dan, sabiendo que es perpendicular.
Para ello, vamos a obtener la pendiente de la recta que nos dan, poniéndola en su forma explícita:
La pendiente de esta recta es:
La pendiente de una recta perpendicular a esta otra es:
Por lo que la pendiente de una recta perpendicular a la que nos da es:
Con esta pendiente y sabiendo que pasa por el punto:
Utilizamos la ecuación punto pendiente para calcular la ecuación de la recta:
Sustituimos las coordenadas del punto y la pendiente por sus valores:
Operamos para eliminar el paréntesis:
Y despejamos la "y":
Agrupamos los números teniendo en cuenta que tenemos fracciones por lo que antes hay que reducir a común denominador:
Finalmente, la ecuación explícita de la recta queda:
Ejercicio 8
Considera la recta de ecuación y=-2x+2. Busca las coordenadas del punto de intersección de esta recta con la recta perpendicular a ella que por el punto P (6,3)
Tenemos la recta:
Tenemos que calcular la ecuación de otra recta que sea perpendicular a ella y pase por el punto P, por tanto, vamos a calcular la pendiente de la nueva recta.
La pendiente de la recta que nos dan es:
La pendiente de una recta perpendicular a otra es:
Que en nuestro caso sería:
Ahora vamos a calcular la ecuación de una recta con esta pendiente y pase por el punto:
Mediante la ecuación punto pendiente:
Sustituimos los valores de las coordenadas del punto y de la pendiente:
Operamos para eliminar el paréntesis:
Simplificamos la fracción que nos queda en el segundo miembro:
Despejamos "y" pasando el 3 sumando al segundo miembro:
Y operamos:
Esta es la ecuación de la recta perpendicular a la dada que pasa por el punto P (6,3).
Ahora vamos a calcular el punto de intersección entre las dos rectas. Para ello hay que resolver el sistema formado por ambas ecuaciones:
Tenemos un sistema de dos ecuaciones con dos incógnitas, que lo resolveré en este caso por el método de igualación.
Para ello igualo los dos segundos miembros de ambas ecuaciones, ya que ambas son iguales a "y":
Ahora tengo que despejar x. Paso los términos con x al primer miembro y los términos sin x al segundo miembro:
Elimino denominadores:
Agrupo términos en el primer miembro:
Y despejo x:
Este valor de x lo sustituyo en una de las dos ecuaciones para obtener el valor de "y".
Voy a tomar por ejemplo la segunda ecuación:
Sustituyo la x por 4/5 y opero:
El valor de "y" es 2/5.
Por tanto, el punto de intersección, que llamaremos A por ejemplo, tiene de coordenadas las soluciones del sistema que forman ambas ecuaciones, que es:
Ejercicio 9
Consideramos la recta r: x=3 y la recta s que pasa por los puntos A (1,2) y B (5,0) ¿Cuáles son las coordenas del punto C que está en la intersección de r y s?
Las coordenadas del punto C son las soluciones del sistema de ecuaciones formado por las rectas r y s que tenemos que resolver.
Vamos a obtener en primer lugar la ecuación de la recta s, que pasa por los puntos:
Utilizaremos para ello la fórmula de la ecuación que pasa por dos puntos:
Sustituimos las coordenadas de los dos puntos en la fórmula:
Y operamos:
Tenemos la ecuación en forma contínua, pero la vamos a pasar a su forma implícita para facilitar los cálculos a la hora de resolver el sistema de ecuaciones.
Pasamos cada denominador multiplicando al miembro contrario:
Operamos para eliminar paréntesis:
Pasamos todos los términos al primer miembro, agrupamos y reordenamos:
Ya tenemos la ecuación de la recta s, por lo que podemos formar el sistema de ecuaciones:
En este caso, ya tengo el valor de x, que lo da la primera ecuación. Por tanto, en la segunda ecuación:
Sustituyo la x por 3:
Y ahora operamos para despejar "y":
Las soluciones del sistema son:
Que corresponden con las coordenadas del punto C, que está en la intersección de las rectas r y s:
Ejercicio 10
Calcula la ecuación explícita de la recta que pasa por el punto P (2,2) y es paralela a la recta de ecuaciones paramétricas:
De las ecuaciones paramétricas obtenemos el punto por donde pasa y el vector de dirección de la recta:
Con estos datos, obtenemos la ecuación contínua de la recta:
La cual la vamos a pasar a su forma explícita para obtener su pendiente. Para ello, pasamos los denominadores multiplicando al miembro contrario:
Operamos para eliminar paréntesis:
Despejamos la "y":
Y separamos el segundo miembro en un término con x y otro sin x:
De donde obtenemos la pendiente de la recta que es:
Con esta pendiente y junto con el punto que nos da el resultado:
Vamos a calcular la ecuación de la recta que nos piden, mediante la ecuación punto pendiente:
Sustituimos los datos de la pendiente y de las coordenadas del punto en la ecuación:
Operamos para eliminar el paréntesis del segundo miembro:
Simplificamos la fracción del segundo miembro:
Y finalmente pasamos el -2 sumando al segundo miembro, obteniendo así su ecuación explícita:
Si quieres aprender como obtener todas las ecuaciones de la recta paso a paso, te recuerdo que lo tienes explicado en, el Curso de Geometría Analítica en el Plano, con ejercicios resueltos.
¿Necesitas ayuda con las matemáticas? ¿Quieres que te explique cualquier duda que te surja paso a paso?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: