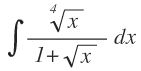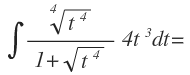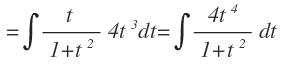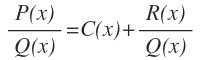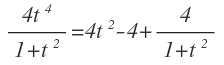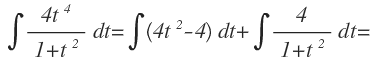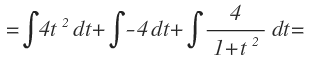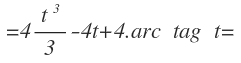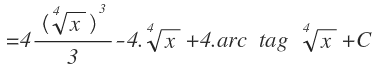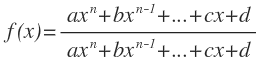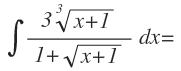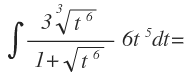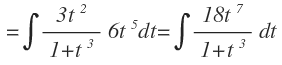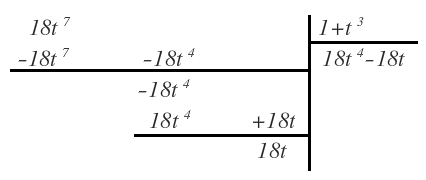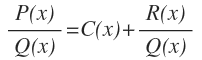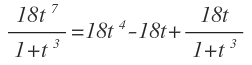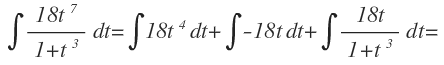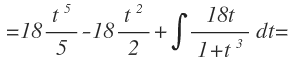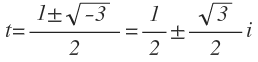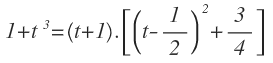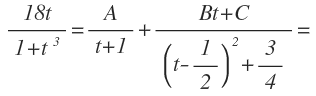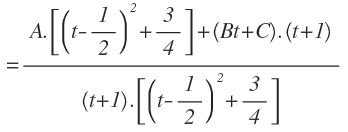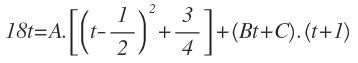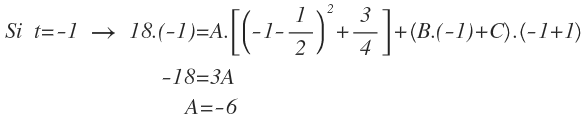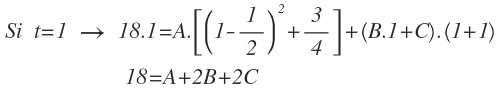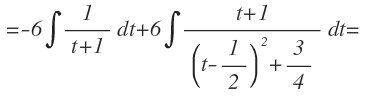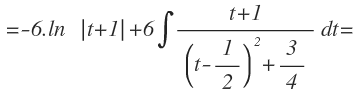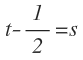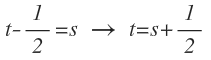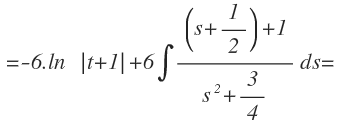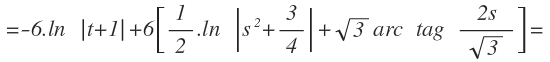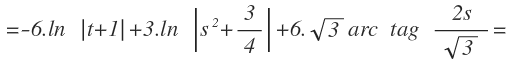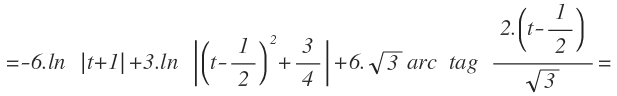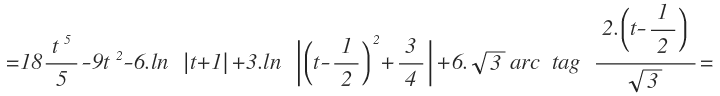Cómo resolver integrales irracionales. Integrales con radicales. Ejercicios resueltos.

A continuación te voy a explicar cómo resolver integrales irracionales, es decir, cómo integrar funciones donde aparecen radicales.

Veremos cómo se resuelven dos tipos de integrales irracionales: cuando dentro de la raíz aparece una potencia de base x (x elevado a un número) y cuando dentro de la raíz hay una función que depende de x, elevada a un exponente.

Vamos a empezar por el primer tipo.

Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.

Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:

QUIERO APRENDER MATEMÁTICAS

Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.

Integrales irracionales con una potencia de base x dentro del radical

Cuando en la integral tenemos términos que corresponde a raíces de cualquier índice, cuyo contenido es una potencia de base x, es decir, la función tiene términos del siguiente tipo:

Entonces se realiza el siguiente cambio de variable:

Donde el exponente «a» corresponde al mínimo común múltiplo de los índices de las raíces:

Vamos a resolver un ejemplo de este tipo:

En este caso, tenemos términos con radicales cuyo contenido está formado por una potencia de base x, en este caso de x elevado a 1, por tanto, realizamos el cambio de variable correspondiente:

Vamos a calcular el exponente «a» al que hay que elevar la «t», que es el mínimo común múltiplo de los índices de las raíces, que en este caso son 2 y 4:

Por tanto, el cambio de variable que hay que realiza es:

Derivamos en ambos miembros de la ecuación anterior para obtener el equivalente de dx con la nueva variable:

Y sustituimos x y dx por sus correspondientes expresiones en función de t:

Operamos en los términos con radicales y después multiplicamos le numerador de la fracción por el factor por el que se está multiplicando:

Hemos llegado a una integral racional donde grado del numerador es mayor que el grado del denominador.

Tienes explicadas cómo resolver integrales de este tipo, al detalle, paso a paso en el Curso de Integrales Indefinidas.

La resolvemos aquí explicando los pasos brevemente.

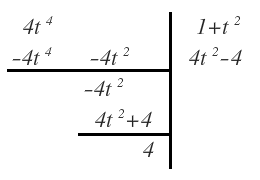
El primer paso para resolverla es realizar la división de los polinomios correspondientes al numerador y al denominador utilizando el método general de la división de polinomios:

Expresamos la función racional en función de los elementos de su división, mediante la siguiente fórmula:

Y queda:

Por lo que podemos expresar la integral como la suma de las integrales de los términos que hemos obtenido:

Que se resuelven mediante la aplicación de las fórmula de integrales inmediatas y nos queda:

Una vez resuelta la integral con respecto de t, tenemos que deshacer el cambio de variable y volver a expresar t en función de x. Obtenemos el valor de t en función de x despejando la x de la expresión utilizada para realizar el cambio de variable:

Y por último, sustituimos t por su valor en función de x para llegar al resultado final:

Integrales irracionales con funciones dentro del radical

Vamos a ver ahora cómo resolver el segundo tipo de integrales irracionales: integrales de funciones que tengan términos con radicales de cualquier índice, cuyo contenido es una función que depende de x elevada a un exponente:

Donde f(x) puede ser o una función polinómica o una función racional, cuyos numerador y denominador también son funciones polinómicas:

En este caso, para realizar el cambio de variable que hay que igualar la función a «t» elevada a un exponente «a»:

Donde, igual que en el caso anterior, el exponente «a» se corresponde con el mínimo común múltiplo de los índices de los radicales:

Para poder aplicar este cambio de variable, la función que está dentro del radical debe ser la misma en todos los términos que aparecen en la integral.

Vamos a verlo más despacio con un ejemplo. Vamos a resolver la siguiente integral:

En este caso, tenemos dos términos con radicales, que tienen dentro la misma función. Por tanto, realizamos el cambio de variable igualando a «t» elevado a «a», la función que hay dentro de los radicales:

Donde el exponente»a» es el mínimo común múltiplo de los índices 2 y 3:

Así que, el cambio de variable a realizar es:

En esta expresión, derivamos en ambos miembros para obtener la equivalencia de dx en función de t:

Sustituimos x y dx por sus correspondientes expresiones en función de t y queda:

Y operamos:

Nos ha quedado una vez más, una integral racional, donde el grado del numerador es mayor que el grado del denominador, así que para resolverla, dividimos el numerador y el denominador con el método general:

Expresamos la función racional en función de los elementos de su división:

Por lo que la integral, podemos escribirla como la suma de las integrales de estos nuevos términos:

Las dos primeras integrales las resolvemos mediante aplicación de fórmula de integrales inmediatas:

La tercera integral se trata de una integral racional, donde el grado del numerador es menor que el grado del denominador, por lo que la resolveremos a parte:

En primer lugar descomponemos el denominador utilizando la regla de Ruffini, al ser de tercer grado y nos queda:

Uno de los factores es un polinomio de segundo grado irreducible, cuyas raíces son complejas:

Por lo que vamos a aplicar el método de integración de funciones racionales con raíces complejas en el denominador.

Para ello, expresamos el polinomio de segundo grado en función de sus soluciones complejas:

Y queda:

Por lo que la descomposición en factores, expresando el polinomio irreducible de esta nueva forma nos queda:

Descomponemos la función racional como una suma de fracciones simples, cuyos denominadores corresponden con cada uno de los factores del denominador original. El numerador de la primera fracción es una constante y el numerador de la segunda fracción es un polinomio de grado 1:

Sumamos ambas fracciones reduciéndolas a denominador común:

Ahora, igualamos el numerador de la función racional con el numerador que acabamos de obtener:

Utilizamos esta expresión para calcular las constantes A, B y C, dándole valores a t:

Le damos t=-1 para que se anule el segundo término y obtengamos directamente el valor de A:

Le damos t=0 para que se anule el término B.t y de esta forma obtenemos una expresión en función de A y C:

Como ya sabemos el valor de A, podemos obtener el valor de C:

Finalmente, le damos otro valor a t, como por ejemplo t=1 y obtendremos una expresión en función de A, B y C:

Como ya conocemos el valor de A y C, los sustituimos por su valor en la última expresión y despejamos el valor de B:

Sustituimos los valores de A, B y C en las fracciones simples:

Como consecuencia, podemos escribir la integral como la suma de las integrales de las fracciones simples:

Sacamos fuera las constantes:

La primera integral se puede resolver con la fórmula de la integral inmediata de la función logarítmica:

Para calcular la segunda integral, debemos realizar un nuevo cambio de variable. Al contenido del paréntesis del denominador le llamamos «s»:

Derivamos en ambos miembros para obtener la equivalencia de dt en función de s:

Y de la primera expresión, podemos despejar cuál es el valor de «t» en función de «s»:

Realizamos el nuevo cambio de variable en la integral y queda:

Operamos en el numerador de la integral:

Separamos la integral es dos nuevas integrales, una por cada término del numerador:

La primera integral puede resolverse por medio de la integral inmediata de una función potencial, por lo que le añadimos un 2 al numerador y por tanto, añadimos otro 2 dividiendo.

En la segunda integral sacamos fuera la constante y sacamos factor común a 3/4, para conseguir un +1:

La primera integral la dejamos igual de momento y en la segunda integral expresamos el primer término del paréntesis como un sólo término al cuadrado. Para ello, dentro del paréntesis hacemos la raíz cuadrada tanto en el numerador como en el denominador, y nos queda:

Ahora aplicamos la fórmula de la integral inmediata de la función logarítmica en la primera integral y la de la función arco tangente en la segunda integral:

Multiplicamos el 6 por cada uno de los términos del corchete:

Y deshacemos el cambio de variable, volviendo a expresar «s» en función de «t»:

No nos olvidemos de que esta integral formaba parte de las tres integrales en las que habíamos separado la integral en función de «t»:

Donde ya habíamos resuelto las dos primeras integrales mediante la aplicación de integrales inmediatas y ahora sustituimos la tercera integral por su resultado:

Por último, tenemos volver a deshacer el cambio de variable, expresando «t» en función de «x», que obtenemos ese valor despejando la «t» de la primera expresión que utilizamos para obtener el cambio de variable:

Sustituimos la «t» por su valor en función de «x» y, ahora sí que sí, hemos llegado al resultado final.

Como ves, para resolver estos tipos de integrales irracionales es necesario que sepas resolver perfectamente todos los tipos de integrales racionales previamente, las cuales las tienes explicadas paso a paso en el Curso de Integrales Indefinidas.

Queda pendiente por explicar las integrales irracionales que se resuelven mediante sustitución trigonométrica, las cuales las tienes explicadas dentro del curso.

¿Necesitas ayuda con las matemáticas? ¿Quieres que te explique cualquier duda que te surja paso a paso?

Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.

He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.

Con mi método:

• Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
• Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión

Suena bien ¿no?

¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?

Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más:

ENSÉÑAME MATEMÁTICAS