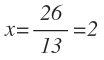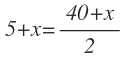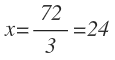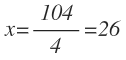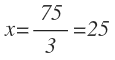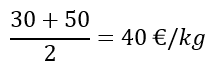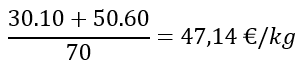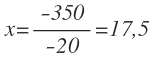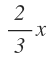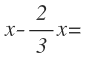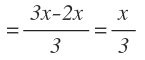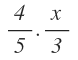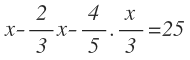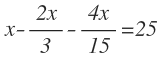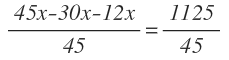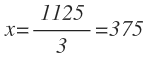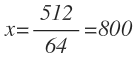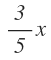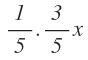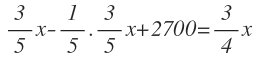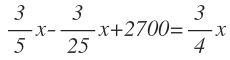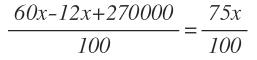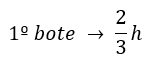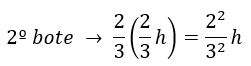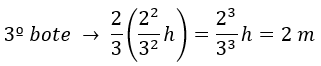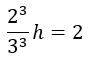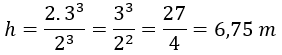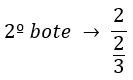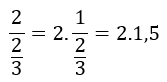A continuación te voy a explicar cómo resolver problemas de ecuaciones de primer grado. Te explicaré cómo plantear la ecuación paso a paso, a interpretar la solución obtenida, así como a comprobar si tu resultado es correcto.
¡Empezamos!
Si has llegado hasta aquí es porque quieres aprender a resolver algún ejercicio. ¿Has pensado en apuntarte a clases de matemáticas online?. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Procedimiento general para la resolución de problemas de ecuaciones de primer grado
El procedimiento para resolver problemas de ecuaciones de primer grado es el siguiente:
- Identificar las incógnita del problema: Debemos saber qué es lo que nos está preguntando el problema
- Asignar la variable x a la incógnita del problema.
- Plantear la ecuación de primer grado traduciendo el enunciado a lenguaje algebraico
- Resolver la ecuación de primer grado
- Interpretar la solución: Una vez tenemos la solución de la ecuación (que no es la solución del problema), debemos interpretarla para darle un sentido, obteniendo así la solución del problema
Problemas de ecuaciones de primer grado (con solución)
Vamos a ver resolver ahora unos cuantos problemas resueltos de ecuaciones de primer grado siguiendo el procedimiento que te acabo de describir. Veremos cómo resolver diferentes tipos de problemas.
Doy por hecho que saber resolver ecuaciones de primer grado. Si no es tu caso y necesitas a aprender, te recomiendo que empieces el Curso de Ecuaciones de Primer Grado desde el principio, en el que te enseño paso a paso cómo resolverlas.
Problemas resueltos de cantidades o precios
Problema 1
La suma de tres números naturales consecutivos es igual a cuádruple del menor ¿De qué números se trata?
Nos preguntar por tres números. Empezamos llamando x al primer número:
El enunciado nos dice que son tres números consecutivos. Los números son consecutivos (1, 2, 3, 4…)cuando el número siguiente es una unidad mayor que el anterior. Entonces, si el primer número es x, el segundo número será una unidad más, es decir, x+1:
Y siguiendo el mismo razonamiento, el tercer número será una unidad mayor que el segundo, es decir, x+2:
Por tanto, los tres números traducidos al lenguaje algebraico son:
Traducimos a lenguaje algebraico el enunciado: La suma de tres números consecutivos es decir, x+(x+1)+(x+2), es igual al cuádruple del menor. El menor es el primer número, x, y su cuádruple es 4x. La ecuación queda:
Ahora pasamos a resolverla. En primer lugar eliminamos los paréntesis, que como los precede un signo +, los términos que quedaban dentro no varían:
Pasamos los términos con x al primer miembro y los números al segundo miembro:
Operamos en cada miembro:
Multiplicamos ambos miembros por -1, para que la x quede positiva en el primer miembro (hay otras formas de resolverlo). La solución por tanto es:
Pero ésta es la solución de la ecuación. Tenemos que encontrar la solución del problema. Sustituimos el valor de la x en nuestras expresiones de los tres números traducidos a lenguaje algebraico.
El primer número es:
El segundo número es:
El tercer número es:
Vamos a comprobar que el resultado es correcto. La suma de los tres números es:
Y el cuádruple del menor, es decir, del primer número es:
Su resultado es el mismo, luego el enunciado se cumple y por tanto, nuestra solución es correcta.
Problema 2
Por un videojuego, un cómic y un helado, Jaime ha pagado 26 euros. El videojuego es 5 veces más caro que el cómic y el cómic cuesta el doble que el helado. ¿Cuánto ha pagado Jaime por cada artículo?
Nos preguntan por el precio de cada artículo, pero en este caso, tenemos 3 artículos ¿A cuál le llamamos x?
Nos dan datos del videojuego, diciendo que es más caro que el cómic. También nos dan datos del cómic, diciendo que cuesta el doble que el helado, pero sin embargo no nos dan ningún dato del helado. Por tanto, al helado le llamamos x:
En problemas de este tipo, hay que llamar x al artículo del que no tengamos ningún dato.
Una vez sabemos qué artículo es x, traducimos a lenguaje algebraico el resto de artículos, volviendo hacia atrás en el enunciado.
Del cómic nos dice que cuesta el doble que el helado, como el helado es x, el cómic será 2x:
Del videojuego nos dice que cuesta 5 veces más que el cómic. Como el cómic es 2x, el videojuego será 5.2x, o lo que es lo mismo 10x:
Ahora planteamos la ecuación. El precio de los tres artículos, es decir, la suma de los tres, es igual a 26 euros:
Empezamos a resolverla operando en el primer miembro:
Y pasamos el 13 dividiendo al segundo miembro:
El valor de x es 2, pero no es la solución del problema. Tenemos que sustituir la x por su valor, en cada una de las expresiones de los artículos.
Para el helado:
Para el cómic:
Para el videojuego:
Luego el videojuego vale 20 euros, el cómic 4 euros y el helado 2 euros, que si los sumas su resultado es 26 euros.
Problema 3
Me falta 1 euro para comprar mi revista preferida. Si tuviera el doble de lo que tengo ahora, me sobrarían 2 euros. ¿Cuánto tengo? ¿Cuánto vale la revista?
Este problema es algo más complejo que los anteriores.
Vamos a empezar llamándole x al dinero que tengo:
También nos preguntan por el precio de la revista, que lo expresaremos en función del dinero que tengo. Si tengo x dinero y me falta 1 euros para comprarla, quiere decir, que la revista vale 1 euro más de lo que tengo, luego la revista será x+1:
Ya tenemos traducido a lenguaje algebraico el dinero que tengo y el precio de la revista.
Ahora con la segundo parte del problema, vamos a plantear al ecuación. Dice así: Si tuviera el doble de lo que tengo ahora, me sobrarían 2 euros.
El doble de lo que tengo es 2x, que tiene que ser igual a lo que vale la revista (x+1) más 2 euros que me sobran, es decir, x+1+2. La ecuación queda:
Para entender que el +2 va en el segundo miembro, piensa que 2x es 2 unidades mayor que x+1 (ya que al comprar la revista me sobran 2 euros), entonces, para igualar ambos miembros, necesito sumar 2 al segundo miembro.
Resolvemos la ecuación pasando los términos con x al primer miembro y los términos si x al segundo miembro:
Operamos y queda:
Luego el dinero que tengo es:
Y el precio de la revista es:
El resultado es correcto porque vemos que al tener 3 euros, me falta 1 euro para comprar la revista. Si tuviera el doble, es decir, 6 euros, me sobrarían 2. Por tanto, se cumple la condición del enunciado.
Problemas resueltos de edades
Problema 1
Antonio tiene 15 años, su hermano Roberto 13 y su padre 44. ¿Cuántos años tienen que pasar para que entre los dos hijos iguales la edad del padre?
Empezamos asignando a cada uno la edad que tiene:
Nos preguntan los años que tienen que pasar, luego llamamos x a los años que pasan.
Dentro de x años, cada uno tendrá x años más, luego para saber los años que tendrá cada uno dentro de x años, le sumamos x a cada uno:
El enunciado nos dice que dentro de x años, la suma de las edades de los hijos será igual a la edad del padre, luego utilizando las expresiones de los años de cada uno, dentro de x años, la ecuación queda:
Empezamos a resolverla pasando los términos con x al primer miembro y los números al segundo miembro:
Operamos en ambos miembros, llegando a la solución de la ecuación.
En este caso, x que son los años que pasan, es igual a 16. Luego la solución de la ecuación coincide con la solución del problema.
Dentro de 16 años cada uno tendrá estos años:
Que efectivamente, si sumamos las edades de los hijos, su resultado es igual a la edad del padre:
Problema 2
El padre de Pedro tiene 40 años y él tiene 5. ¿Dentro de cuantos años la edad de Pedro será la mitad que la de su padre?
Asignamos a cada uno la edad que tiene:
Llamamos x a los años que pasan.
Dentro de x años, cada uno tendrá la edad que tiene actualmente más x:
El enunciado nos dice que dentro de x años, la edad de Pedro será la mitad que la de su padre, luego:
Para entender que la edad del padre hay que dividirla entre 2 en la ecuación, piensa que si no dividimos ninguna, la edad de Pedro es la mitad que la de su padre (o la edad de su padre es el doble que la de Pedro), por lo que para que se cumpla la igualdad, tenemos que dividir la edad del padre entre 2.
Para empezar a resolver la ecuación, pasamos el 2, que está dividiendo a todo el segundo miembro, multiplicando al primer miembro:
Multiplicamos el 2 por el paréntesis:
Pasamos los términos con x al primer miembro y los términos sin x al segundo miembro:
Y operamos llegando a la solución:
Por tanto, deben pasar 30 años para que la edad de Pedro sea la mitad que la de su padre.
Vamos a comprobarlo. Dentro de 30 años, cada uno tendrá la siguiente edad:
Efectivamente, se cumple que Pedro tendrá 35 años, que es la mitad de los 70 que tendrá su padre
Problema 3
Sabemos que mi tío tiene 27 años más que mi primo y que dentro de 12 años le doblará la edad. ¿Cuántos años tiene cada uno?
El problema nos dice que el tío tiene 27 años más que el primo, pero del primo no nos da ningún dato, luego a la edad del primo le llamamos x:
Sabiendo que la edad del primo es x, la edad del tío es 27 años más, luego la edad del tío es:
El enunciado dice que dentro de 12 años el tío le doblará la edad al primo. Tenemos que plantear la ecuación con esta frase.
En primer lugar vamos a obtener la edad que tendrá cada uno de ellos dentro de 12 años y para ello sumamos 12 a cada una de las edades.
La edad del primo será:
Y la edad del tío será:
La edad del tío es el doble que la del primo, por tanto, para que las edades sean iguales, hay que multiplicar por 2 la edad del primo:
Una vez planteada la ecuación pasamos a resolverla. Empezamos eliminando el paréntesis:
Pasamos los términos con x a un miembro de la ecuación y los números al otro:
Finalmente operamos y resolvemos:
Ahora este valor de x los sustituimos en cada una de las edades:
Problema 4
La edad de un padre es el doble que la de su hijo. Sabiendo que dentro de 6 años la suma de sus edades será de 84 años, calcular la edad actual del padre y del hijo.
El enunciado nos da la referencia de que la edad del padre es el doble que la de su hijo. Como del hijo no nos dan ningún dato, a la edad del hijo le llamamos x:
Una vez sabemos que la edad del hijo es x, la edad del padre es el doble, es decir, 2x:
El problema nos dice que dentro de 6 años, la suma de las edades será de 84. Vamos a traducir a lenguaje algebraico esa expresión.
Lo primero que tenemos que hacer es obtener la edad de cada uno dentro de 6 años. Para ello, le sumamos 6 a cada una de las edades.
La edad del hijo es:
Y la edad del padre es:
Ahora sumamos estas dos edades y las igualamos a 84:
Ya tenemos planteada la ecuación. Ahora pasamos a resolverla.
Dejamos en el primer miembro los términos con x y en el segundo miembro los términos sin x:
Agrupamos términos:
Despejamos x y resolvemos:
Este valor de x, lo sustituimos en cada una de las edades iniciales para obtener la edad de cada uno:
Problemas geométricos resueltos
Problema 1
Calcula las dimensiones de un rectángulo en el que la base mide 2 cm menos que la altura y cuyo perímetro es igual a 100 cm.
En primer lugar vamos a asignar las incógnitas. Nos dan datos sobre la base, pero de la altura no nos dicen nada, luego a la altura le llamamos x:
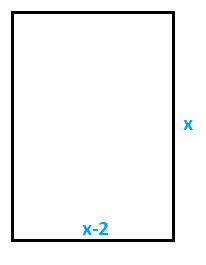
Nos dicen que la base es 2 cm menor que la altura, luego si la altura es x, la base será x-2:
El rectángulo queda de la siguiente manera:
El perímetro es la suma de todos los lados y es igual a 100. Tenemos dos bases y dos alturas, por lo que la ecuación queda:
Eliminamos los paréntesis. Los términos se quedan igual:
Pasamos los términos con x al primer miembro y los términos sin x al segundo miembro:
Operamos en ambos miembros:
Despejamos x y resolvemos:
Sustituimos este valor de la x en las expresiones de la base y la altura. Por tanto la altura mide:
Y la base:
Problema 2
En un triángulo isósceles, cada uno de los lados iguales mide 3 cm más que el lado desigual. Si su perímetro mide 81 cm, ¿cuánto mide cada lado?
Nos dan datos de los lados iguales, pero no del lado desigual. Por tanto, al lado desigual, que es la base, le llamamos x:
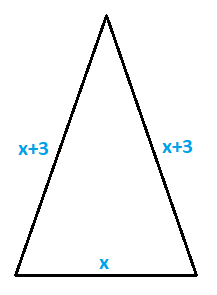
Nos dicen que los lados iguales miden 3 cm más que la base, luego si la base es x, cada lado igual será x+3:
El triángulo sería:
El perímetro, que es la suma de los tres lados, es igual a 81:
Eliminamos paréntesis:
Pasamos los términos con x al primer miembro y los números al segundo miembro:
Operamos en ambos miembros:
Despejamos x y resolvemos:
El valor de x lo sustituimos en la expresión de la base:
Y en el de los lados iguales:
Problemas resueltos de mezclas
Problema 1
En un bar tienen dos clases de café: el café de clase 1 a 30 €/kg y el café de clase 2 a 50 €/kg. ¿Cuántos kg de café hay que mezclar de cada clase para tener 70 kg de café de 45 €/kg?
Antes de empezar a resolver el problema, te voy a explicar más despacio cómo se obtiene la ecuación para que lo entiendas mejor.
Nos preguntan los kg de café que hay que mezclar de cada clase para obtener 70 kg de café mezcla a 45 €/kg, es decir, mezclando cafe 1 con café 2, queremos obtener 70 kg de café de mezcla.
Por ejemplo, si mezclamos el 50% de cada clase de café tendríamos que mezclar 35 kg de cada clase para obtener los 70 kg:
El precio de la mezcla sería 40 €/kg, que corresponde a la media de los precios de las dos clases de café:
Si sumamos la multiplicación del peso por el precio de cada clase de café tenemos:
Que es igual al precio por el peso de la mezcla:
Por tanto, nos queda que:
Vamos a poner otro ejemplo. Ahora mezclamos 10 kg del café tipo 1 y 60 kg del café clase 2, para tener los 70 kg de la mezcla:
En este caso, el precio de la mezcla estaría más cerca del café clase 2 ya que se ha usado más café de ese tipo en la mezcla. Para obtener el precio de la mezcla calculamos su media ponderada (esto no es necesario que lo aprendas, solo lo hago para calcular el precio del ejemplo):
Sumando la multiplicación del peso por el precio de cada café nos da:
Que vuelve a ser igual al precio por el peso de la mezcla:
Así que de nuevo se cumple:
Siempre se cumplen estas tres premisas:
- El peso de la mezcla es igual a la suma de los pesos
- El precio €/kg de la mezcla depende de la clase de café que más cotenga la mezcla.
- La suma de los €/kg por el peso de cada clase es igual a los €/kg de la mezcla por el peso de la mezcla:
En este problema, no sabemos la cantidad de cada café que hay que mezclar. Sólo sabemos el peso de la mezcla. Por eso, a uno de las dos clases de café le llamamos x.
En este caso, podemos llamarle x al café de clase 1 o al café de clase 2. Yo le llamaré x al café de clase 1:
Tenemos que obtener en total 70 kg, sumando los pesos de las dos clases de café. Por tanto, si el café de clase 1 es x, el café de clase 2 será 70-x:
Cuando planteamos una ecuación, debemos trabajar sólo con una media. En este caso, tenemos dos unidades de medida: el peso del café en kg y el precio del café en €/kg. Si multiplicamos el peso por el precio, el resultado será en € y tendremos la misma unidad para cualquier clase de café (clase 1, clase 2 o mezcla).
De esta forma, si sumamos los kilos de café de clase 1 (x) por su precio más los kilos de café de clase 2 (70-x) por su precio, el resultado serán los 45 kg de café mezclado, por su precio, que son 70 €/kg
En problemas de mezclas, la ecuación se plantea operando con las multiplicaciones de pesos por precios.
Vamos a resolver la ecuación. En primer lugar eliminamos el paréntesis multiplicando los términos que tiene en su interior por 50:
Dejamos los términos con x en el primer miembro y los números en el segundo miembro:
Operamos en ambos miembros:
Despejamos x y resolvemos:
Por tanto, necesitaremos 17,5 kg de café de clase 1 y 52,5 kg de café de clase 2:
Problema 2
Un químico dispone de dos garrafas de ácido, una con una concentración del 5 % y otra con una concentración del 30 %. ¿Qué cantidad habrá que poner de cada garrafa para conseguir un litro de mezcla con una concentración del 10 %?
Le llamamos x a la cantidad de ácido con una concentración del 5%:
Como en total debemos conseguir una mezcla de 1 litro, si tenemos x litros de ácido al 5%, la cantidad de ácido al 30% será la diferencia hasta llegar a 1 litro, es decir, 1-x:
Para plantear la ecuación debemos operar con los litros de ácido. Entonces, si en cada garrafa multiplicamos la concentración de ácido (en tanto por uno), por los litros de esa garrafa, obtendremos los litros de ácido.
Para calcular los litros de ácido de la primera garrafa tendremos que multiplicar la concentración de ácido en tanto por uno, que es 0,05, por los litros de esa garrafa que son x. Para la segunda garrafa, multiplicamos 0,3 por los litros, que son (x-1). La suma de estas dos cantidades de ácido será igual a la concentración de 0,1 por 1 litro.
En forma de ecuación nos queda:
Vamos a resolver la ecuación.
En primer lugar eliminamos el paréntesis:
Dejamos los términos con x en el lado izquierdo de la ecuación y los que no llevan x en el lado derecho:
Y finalmente despejamos x:
Por tanto, necesitaremos 0,8 litros de ácido al 5% y 0,2 litros de ácido al 30%
Problemas resueltos de porcentajes y fracciones
Problema 1
De una cesta de manzanas se pudren los 2/3 y nos comemos los 4/5 del resto. Si sobran 25 manzanas, ¿cuántas manzanas había en la cesta?
Llamamos x a la cantidad de manzanas:
Ahora vamos a ir traduciendo poco a poco el enunciado a lenguaje algebraico.
Se pudren los 2/3 es decir:
Nos comemos los 5/4 del resto, es decir, de las que quedan después de que se pudran los 2/3. Vamos a calcular primero las que quedan, que lo hacemos restando al total, que es x, las que se pudren, que son 2/3x:
Operamos y nos queda:
Los 4/5 del resto son:
Por tanto, al total le restamos las que se pudren y las que nos comemos. Su resultado es igual a 25:
Ya tenemos la ecuación planteada. Pasamos a resolverla empezando por multiplicar fracciones:
Obtenemos denominador común:
Eliminamos denominadores:
Operamos en ambos miembros:
Despejamos x y resolvemos:
Por tanto, en la cesta había 375 manzanas.
Problema 2
En la primera prueba de una oposición queda eliminado el 52% de los participantes. En la segunda prueba, se elimina al 25% de los restantes. Si el número total de personas eliminadas es de 512, ¿cuántas personas se presentaron a la oposición?
Llamamos x al número de personas:
Ahora vamos traduciendo a lenguaje algebraico el enunciado.
El 52% de los participantes es (revisa la lección sobre cálculo de porcentajes del curso de proporcionalidad para que te quede más claro):
Después se elimina el 25% de los restantes. Vamos a calcular primero los restantes, que lo hacemos restando al total el 52% que hemos calculado antes:
El 25% de los restantes es:
Las personas eliminadas son el 52% de la primera prueba más el 25% de los restantes en la segunda prueba y su suma es igual a 512. Con estos datos planteamos la siguiente ecuación:
Operamos en el primer miembro:
Despejamos x y resolvemos:
A la oposición se presentaron 800 personas.
Problema 3
En el mes de agosto un embalse estaba a los 3/5 de su capacidad. En septiembre no llovió y se gasto 1/5 del agua que tenía. En octubre se recuperaron 2700 m³, quedando a los 3/4 partes de su capacidad. ¿Cuál es la capacidad del embalse?
Llamamos x a la capacidad del embalse:
Los 3/5 de su capacidad es:
1/5 del agua que tenía, que son 3/5.x, es:
A los 3/5 de la capacidad, le restamos 1/5 del agua que tenía, le sumamos 2700 m³ y su resultado son las 3/4 partes de su capacidad. La ecuación queda de la siguiente manera:
Multiplicamos fracciones en primer lugar:
Obtenemos denominador común:
Eliminamos denominadores:
Pasamos los términos con x al primer miembro y los números al segundo miembro:
Operamos en el primer miembro:
Despejamos la x y resolvemos, cuyo resultado son 10000 m³, que es la capacidad total del embalse:
Problema 4
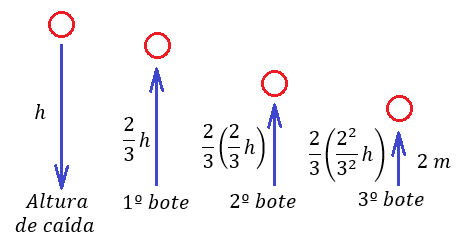
Una pelota de goma cae al suelo y se eleva cada vez que vota a los 2/3 de la altura anterior. Tras botar 3 veces, se ha elevado 2 metros. ¿Desde qué altura cayó?
Este problema lo podemos resolver de dos formas distintas. Vamos a ver cada una de ellas.
Primera forma:
Llamando h a la altura de caída y luego ir multiplicando por 2/3 la altura anterior para calcular la altura de cada bote en función de h.
El esquema sería el siguiente:
Pasamos a detallar el esquema paso a paso:
Partimos de la altura de caída a la que llamamos h:
La altura del primer bote la obtenemos multiplicando por 2/3 la altura anterior que es h:
La altura del segundo bote la obtenemos multiplicando por 2/3 la altura del primer bote:
Y para hallar la altura del tercer bote multiplicamos por 2/3 la altura del segundo bote bote. Además sabemos que esta altura del tercer bote es igual a 2 metros:
Nos queda una ecuación de primer grado que depende de h:
Despejamos h y operamos, resultando que h es igual a una altura de 6,75 metros:
Segunda forma:
Empezamos por la altura conocida del tercer bote e ir hallando la altura de los botes anteriores hasta llegar a la altura de caída.
El esquema sería:
Detallamos el esquema paso a paso:
Sabemos que la altura del tercer bote es igual a 2 metros:
Al igual que para saber la altura del bote siguiente hay que multiplicar por 2/3, para hallar la altura del bote anterior tenemos que dividir entre 2/3. Así que la altura del segundo bote la podemos calcular dividiendo entre 2/3 los 2 metros del tercer bote:
Para que simplificar los cálculos, en vez de ir dividiendo entre 2/3 vamos a multiplicar por 1,5, que es lo mismo. Es decir, dividir entre 2/3 es lo mismo que multiplicar por el inverso de 2/3, que es 1/(2/3) y 1/(2/3) es igual a 1,5:
Así que la altura del segundo bote la obtenemos multiplicando por 1,5 la altura del tercer bote:
La altura del primer bote la obtenemos multiplicando por 1,5 la altura del segundo bote:
Y finalmente, la altura de caída la calculamos multiplicando por 1,5 la altura del primer bote:
Dando el mismo resultado que con la primera forma.
¿Necesitas ayuda en matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: