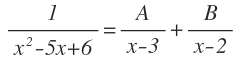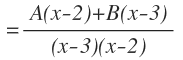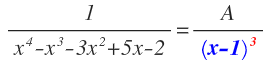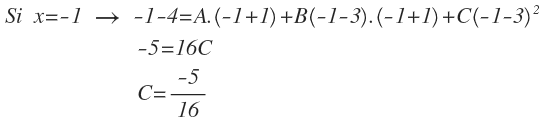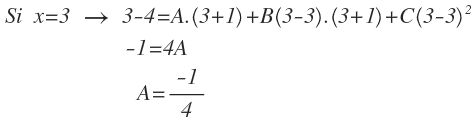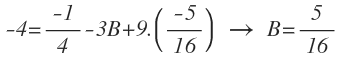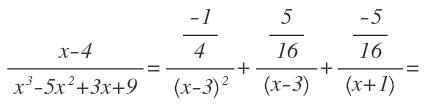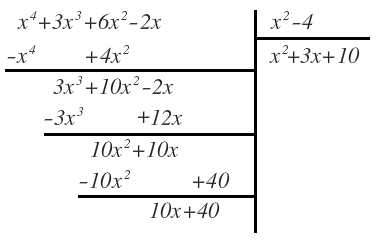Descomposición en fracciones simples. Ejercicios resueltos

A continuación te voy a enseñar cómo descomponer fracciones algebraicas en una suma de fracciones simples, con ejercicios resueltos paso a paso.

¡Empezamos!

Si has llegado hasta aquí es porque seguramente necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolver algún ejercicio que se te resista o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.

Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:

QUIERO APRENDER MATEMÁTICAS

Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.

Cómo descomponer en fracciones simples

Para saber qué procedimiento hay que aplicar para descomponer una fracción algebraica en una suma de fracciones simples, tenemos que fijarnos en los grados, tanto del numerador como del denominador.

Si tenemos una fracción algebraica:

Podemos tener dos casos:

1 – Que el grado del numerador sea menor que el grado del denominador

Si el grado del numerador es menor que el grado del denominador, entonces hay que analizar las raíces del denominador. Pueden darse tres casos:

1.1 – Que el denominador Q(x) tenga raíces reales distintas

1.2 – Que el denominador Q(x) tiene raíces reales múltiples

1.3 – Que el denominador Q(x) tiene raíces complejas

Es decir, en función del tipo de raíces del denominador, se aplicará un procedimiento u otro.

2- Que el grado del numerador sea mayor o igual que el grado del denominador

Si el grado del numerador es mayor o igual que el grado del denominador, entonces tendremos que realizar la división por el método general y después, volver a analizar la fracción resultante para ver qué procedimiento del primer caso aplicar.

Vamos a ver detenidamente cada uno de los casos

Cómo descomponer fracciones algebraicas con grado del numerador menor que el grado del denominador

Vamos ver cómo descomponer una fracción algebraica cuando el grado del numerador es menor que el grado del denominador.

Como descomponer fracciones algebraicas con raíces reales distintas en el denominador

Tenemos la siguiente fracción algebraica:

El grado del numerador es 0 y el grado del denominador es 2, por tanto, el grado del numerador es menor que el grado del denominador

Vamos a proceder a descomponer la fracción en una suma de fracciones simples. En primer lugar, tenemos que factorizar el polinomio del denominador.

En este caso es un polinomio de grado 2. Para descomponerlo hallamos sus raíces (soluciones de la ecuación de segundo grado) y para ello lo igualamos a 0 y resolvemos la ecuación:

Cuyas soluciones son:

En este punto es donde sabemos que el denominador tiene raíces reales distintas.

Cada raíz del polinomio puede escribirse de forma de binomio (x-a), donde a es el valor de cada raíz y además, un polinomio cualquiera puede escribirse como el producto de todos sus binomios (x-a). Por tanto:

Si el polinomio del denominador fuera de grado 3 o superior habría que utilizar otros métodos para descomponerlo. Tienes todos los métodos de descomposición de polinomios explicados paso a paso en el Curso de Polinomios.

Ahora, la fracción algebraica, puede escribirse como una suma de fracciones simples, cuyos denominadores son cada uno de los factores del denominador:

En este caso tenemos dos fracciones porque tenemos dos factores. En general, tendríamos tantas fracciones como factores nos salgan al descomponer el denominador.

Los numeradores de cada fracción son dos constantes que no conocemos, que llamaremos A y B:

Ahora vamos a calcular el valor de A y B.

Tenemos una suma de dos fracciones con distinto denominador. Para poder sumarlas hay que hallar denominador común, que será la multiplicación de los denominadores:

Y para hallar cada nuevo numerador, se divide el denominador común entre el denominador de cada fracción inicial y el resultado se multiplica por el numerador de la fracción inicial:

Y esto lo podemos escribir como una sola fracción:

Y al llegar aquí hemos llegado a la siguiente conclusión: La fracción original es igual a la fracción que acabamos de calcular:

Por tanto, como sabemos que los denominadores son iguales:

Los numeradores también serán iguales:

Nos quedamos con esta última expresión para calcular A y B y para ello, le damos valores a la x.

Los valores que hay que darle a la x son las raíces del polinomio, ya que hará que se anulen A o B y sepamos su resultado. Entonces:

Ahora que sabemos los valores de A y B, los sustituimos en esta expresión que teníamos al principio:

Como descomponer fracciones algebraicas con raíces reales múltiples en el denominador

Para entender este caso, hay que aclarar que el denominador tenga raíces reales múltiples significa que al menos una de sus raíces se repite.

Vamos a ver un ejemplo:

El grado del numerador es 1 y el grado del denominador es 3, por lo que el grado del numerador es menor que el grado del denominador.

Ahora debemos factorizar el denominador. Como es un polinomio de grado tres, utilizamos la regla de Ruffini y nos queda:

Al factorizar podemos ver que x=3 es una raíz repetida del polinomio del denominador, por lo que tenemos raíces reales múltiples y por tanto hay que utilizar este método que te voy a explicar para descomponerla en fracciones simples.

Cuando teníamos raíces reales distintas, los denominadores de las fracciones simples eran cada uno de los factores del denominador de la función racional, pero cuando las raíces son múltiples, en los denominadores de las fracciones simples, debemos poner su factor correspondiente en forma de potencia y luego vamos sumando fracciones simples, cuyo denominadores serán el mismo factor de la raíz múltiple en forma de potencia, pero disminuyendo en uno el exponente, hasta que el exponente sea 1.

Por ejemplo, vamos a descomponer esta fracción algebraica en fracciones simples:

En primer lugar descomponemos el denominador, utilizando la regla de Ruffini al ser un polinomio de grado cuatro:

Nos queda:

Que expresando el factor que se repite en forma de potencia nos queda:

Como te he comentado antes ponemos el factor en forma de potencia como uno de los denominadores de las fracciones simples, es decir, ponemos (x-1)³ como denominador:

Ahora vamos sumando fracciones simples, cuyo denominadores serán el mismo factor de la raíz múltiple en forma de potencia, pero disminuyendo en uno el exponente, hasta que el exponente sea 1:

Y por último añadimos la siguiente fracción simple cuyo resultado corresponde con el factor de la raíz que no se repite:

A este método de obtener fracciones simples se le conoce como el método Alemán.

Bien, una vez hemos dejado claro esto, vamos a aplicar lo aprendido para seguir descomponiendo nuestra fracción algebraica. Nos quedamos en que habíamos factorizado el denominador, llegando a la conclusión de que tenía raíces reales múltiples:

Descomponemos la función racional en fracciones simples aplicando el método alemán: la primera fracción simple tendrá como denominador el factor correspondiente a la raíz repetida en forma de potencia, es decir (x-3)², la siguiente fracción simple será este mismo factor pero con su exponente disminuido en 1, es decir (x-3) y por último añadimos la última fracción simple que tendrá como denominador el factor que corresponde a la otra raíz:

Los numeradores de cada fracción simple son constantes que no conocemos y los hemos llamado A, B y C.

Vamos a obtener el valor de estas constantes.

En primer lugar realizamos la suma de las fracciones simples, reduciendo a común denominador:

Ahora igualamos el numerador de la fracción que acabamos de obtener con el numerador de la fracción original:

El siguiente paso es darle valores a la x. Le vamos a dar los valores de sus raíces, que harán que se anulen términos. Como tenemos tres constantes y sólo dos raíces, nos falta un valor para la x, que será el 0.

Podemos elegir cualquier número para darle valores a la x. Hemos elegido estos para simplificar cálculos.

Con x=-1:

Obtengo directamente el valor de C.

Con x=3:

Obtengo directamente el valor de A.

Con x=0:

Obtengo una ecuación que depende de A, B y C. Como ya sé el valor de A y C, sólo me queda sustituir y despejar para obtener el valor de B:

Una vez conocidos los valores de todas las constantes, escribimos nuestra fracción algebraicas como una suma de fracciones simples:

Como descomponer fracciones algebraicas con raíces complejas en el denominador

El procedimiento que vamos a ver a continuación se utiliza para descomponer fracciones algebraicas cuyo denominador tenga raíces complejas, siendo el grado del numerador menor que el del denominador.

Por ejemplo:

El grado del numerador es menor que el grado del denominador, ya que en el denominador tenemos un polinomio de grado 3, que es el resultado de multiplicar ambos factores:

En nuestro caso, ya tenemos el denominador descompuesto en factores (si no es así, hay que descomponerlo utilizando la regla de Ruffini si es un polinomio de grado mayor o igual a tres).

Uno de los factores es de grado dos, lo que significa que es un polinomio de segundo grado irreducible y que por tanto, sus raíces son complejas. Lo comprobamos igualando el polinomio a cero y resolviendo la ecuación de segundo grado obtenida:

Llegados a este punto, hemos identificado que se trata de una función racional, donde el grado del numerador es menor que el grado del denominador, con raíces complejas.

A la hora de descomponer esta fracción algebraica como una suma de fracciones simples, el denominador de cada fracción simple corresponde a cada factor del denominador original, tal y como se hace cuando descomponemos fracciones con raíces reales distintas:

En las fracciones simples donde el denominador sea un polinomio de grado 1, el numerador corresponderá a una constante que no conocemos, que le llamamos por ejemplo A:

Ahora viene la diferencia de este método: En las fracciones simples cuyo denominador sea un polinomio de segundo grado, el numerador que le corresponde será un polinomio de grado 1, compuesto por un término de grado 1 y un término de grado cero, de los cuales no conocemos sus coeficientes y los debemos calcular. Este polinomio de grado 1 le hemos llamado en este caso Bx+C:

Ahora debemos calcular el valor de las constantes A, B y C.

Para ello, sumamos las fracciones simples, reduciéndolas a común denominador:

La fracción resultante, tiene el mismo denominador que nuestra fracción original:

Por tanto, sus numeradores son iguales:

Y nos quedamos con esta ecuación para hallar los valores de las constantes, que los calcularemos, dando valores a la x y obteniendo nuevas ecuaciones que estarán en función de las constantes y donde podremos despejarlas para obtener su valor.

En primer lugar le daremos a x el valor de la raíz real, para anular uno de los términos y obtener el valor de una de las constantes directamente. Le damos x=1:

Ahora le damos el valor de x=0, para que se anule al menos el término con x correspondiente al polinomio de primer grado que no conocemos. Nos queda:

En este caso, como ya conocemos el valor de A, podemos obtener también el valor de C, que es:

Finalmente, le damos un tercer valor a x, que puede ser cualquiera. Nos quedará una ecuación en función de A, B y C. Yo le he dado x=-1 y me queda:

Como ya conocemos los valores de A y C, los sustituimos por su valor, operamos y obtenemos el valor de B:

Ahora que sabemos los valores de todas las constantes, los sustituimos en sus fracciones simples, por lo que ya tenemos descompuesta en fracciones simples nuestra fracción algebraica:

Cómo descomponer fracciones algebraicas con grado del numerador mayor o igual que el grado del denominador

Ahora voy a explicar cómo se descomponen las fracciones algebraicas como suma de fracciones simples cuando el grado del numerador es igual o mayor que el grado del denominador al mismo tiempo que realizamos un ejemplo paso a paso.

Tenemos la siguiente fracción algebraica:

Se trata de una fracción algebraica donde el grado del numerador es mayor que el grado del denominador, ya que el numerador es de grado 4 y el denominador es de grado 2.

En este caso, el primer paso que hay que realizar es la división de polinomios mediante el método general:

En cualquier división, el dividendo es igual al divisor por el cociente más el resto. En nuestro caso, con polinomios, quedaría de la siguiente manera:

Si en esta última expresión, divido los términos de ambos miembros entre el divisor me queda:

Operando en el primer término del segundo miembro, vemos que Q(x) se anula y finalmente queda:

Con lo que hemos obtenido una nueva forma de expresar una función racional a partir de los elementos de su división, que está formada por dos términos, uno de los cuales corresponde a una nueva fracción, donde el grado del numerador  es menor que el grado del denominador, que es lo que queremos buscar (un poco más abajo sabrás por qué).

En nuestro caso, los polinomios correspondientes al dividendo, el divisor, el cociente y el resto son:

Y aplicando la fórmula anterior, nuestra fracción algebraica nos queda de la siguiente forma:

donde en uno de los términos me ha quedado una fracción algebraica cuyo grado del numerador es menor que el grado del denominador y que a su vez vamos a descomponer en una suma de fracciones simples, utilizando el método antes explicado.

Nos centramos ahora en esta fracción algebraica:

Empezamos descomponiendo el denominador:

Vemos que tiene dos raíces reales distintas, por lo que aplicamos el procedimiento para ese caso, así que el denominador de cada fracción simple corresponde con cada factor del denominador de la función racional y los numeradores corresponden a dos constantes, A y B, las cuales, tenemos que calcular su valor:

Para ello, sumamos ambas fracciones reduciendo a denominador común:

Y después igualamos el numerador de la fracción algebraica con el numerador que de la fracción que acabamos de obtener:

Utilizamos esta última ecuación para obtener los valores de A y B, para lo cual, le damos valores a x, que serán los correspondientes a las raíces del denominador.

Para x=2, sustituimos la x por 2 y nos queda:

Para x=-2, sustituimos la x por -2 y nos queda:

Por último, expresamos la fracción algebraica como la suma de fracciones simples que acabamos de calcular:

Recuerda que estamos descomponiendo esta fracción y nos quedamos en este punto:

Sólo nos queda sustituir la fracción del último término por su descomposición:

Ejercicios resueltos de descomposición de fracciones algebraicas en fracciones simples

Descomponer las siguientes fracciones algebraicas en suma de fracciones simples:

¿Necesitas ayuda en matemáticas? ¿Quieres que te explique cualquier duda que te surja?

Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.

He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.

Con mi método:

• Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
• Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión

Suena bien ¿no?

¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?

Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más:

ENSÉÑAME MATEMÁTICAS