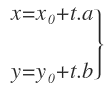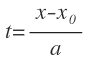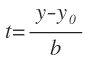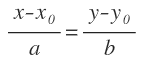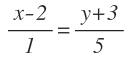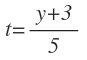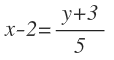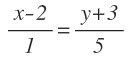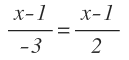A continuación te voy a explicar cómo calcular la ecuación contínua y la ecuación general o implícita de la recta, con ejemplos y ejercicios resueltos paso a paso. Además te explico cómo saber si un punto pertenece a una recta y cómo calcular un punto que pertenezca a una recta.
Las demás formas de expresar la ecuación de una recta, las tienes explicadas paso a paso en el Curso de Geometría Analítica en el Plano, con ejercicios resueltos.
Es importante conocer y dominar todas las formas en las que se puede expresar una recta, ya que eso nos permitirá calcular la ecuación de la recta en función de los datos que conozcamos.
Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Ecuación contínua de la recta
Te voy a explicar cómo obtener la ecuación contínua de una recta, conocido un punto por donde pase y su vector de dirección:
La ecuación contínua se obtiene a partir de las ecuaciones paramétricas:
Para ello, en la primera ecuación:
Despejamos «t»:
Y en la segunda ecuación:
También despejamos «t»:
Ahora, igualamos ambas expresiones de «t», ya que «t» es el mismo valor en ambas ecuaciones, dando lugar a la ecuación contínua de la recta:
Donde X0 e Y0 son las coordenadas del punto por donde pasa la recta y a y b son las coordenadas de su vector de dirección:
Vamos a ver un ejemplo de cómo calcular la ecuación contínua de una recta.
Ejercicio resuelto sobre calcular la ecuación contínua de una recta
Hallar la ecuación contínua de la recta que pasa por el punto P0 (2,-3) y cuyo vector de dirección es v=(1,5).
La recta pasa por el punto:
Y tiene como vector director:
Podemos obtener su ecuación contínua de dos formas.
La primera, más corta, es a partir de la fórmula de la ecuación continua de una recta:
Sustituyendo las coordenadas del punto y del vector de dirección:
Después operamos para eliminar paréntesis, obteniendo la ecuación contínua:
Donde como ves, en los numeradores tenemos las coordenadas del punto por donde pasa la recta y en los denominadores tenemos las coordenadas del vector de dirección.
También puedes calcular la ecuación contínua de al recta, a través de sus ecuaciones paramétricas, obtenidas también a partir de las coordenadas del punto por donde pasa y de su vector de dirección:
De la primera ecuación:
Despejamos «t»:
Y de la segunda ecuación:
También despejamos «t»:
Igualamos ambas expresiones de «t» y nos queda:
En este caso, en el primer miembro, al no tener denominador, es equivalente a tener un 1, que lo añadimos para dejar la ecuación exactamente igual que al forma de la ecuación contínua:
Esta bien que conozcas cómo calcular la ecuación contínua a partir de las ecuaciones paramétricas, ya que en muchos ejercicios tendrás las ecuaciones paramétricas como dato inicial.
Ecuación general o implícita de la recta
Vamos a ver ahora cómo obtener la ecuación general o implícita de una recta, conocidos un punto que pase por la recta y su vector de dirección:
La ecuación general se obtiene a partir de la ecuación continua:
Empezamos pasando la «a» multiplicando al segundo miembro y la «b» multiplicando al primer miembro, para no tener denominadores:
Ahora multiplicamos la «a» y la «b» por los paréntesis:
Pasamos todos los términos al primer miembro, dejando cero en el segundo miembro:
Finalmente, ordenamos la ecuación, de forma que pondremos primero el término con «x», después el término con «y» y finalmente los términos que no tienen variable:
Si al coeficiente que queda delante de la x le llamamos A:
Al coeficiente que queda delante de la «y» le llamamos B:
Y al resto de términos le llamamos C:
Llegamos por tanto a la ecuación general de una recta:
En este caso, el vector de dirección lo podemos obtener en con los coeficientes A y B:
Ya que A y B están calculados a partir de las coordenadas a y b del vector de dirección.
Haciéndolo con números es mucho más sencillo. Vamos a verlo con un ejemplo:
Ejercicio resuelto sobre calcular la ecuación general de una recta
Hallar la ecuación general de la recta que pasa por el punto P0 (2,-3) y cuyo vector de dirección es v=(1,5).
Para hallar la ecuación general, partimos de la ecuación contínua, que la tenemos calculada en el ejemplo anterior:
Pasamos el 1 multiplicando al segundo miembro y el 5 multiplicando al primer miembro:
Multiplicamos paréntesis:
Pasamos todos los términos al primer miembro:
Operamos y ordenamos términos, poniendo en primer lugar el término con x, en segundo lugar el término con «y» y en último lugar el número, obteniendo así la ecuación general de la recta (o ecuación implícita).
Como pasar de la ecuación general a las demás
Si tenemos la ecuación general de una recta, ¿cómo podemos calcular el resto de ecuaciones de la recta?, es decir, ¿cómo podemos obtener la ecuación vectorial, las ecuaciones paramétricas y la ecuación contínua?
Para poder calcular el resto de ecuaciones necesitamos tener el vector de dirección y saber un punto que pase por la recta.
Vamos a ver cómo hacer esto con un ejemplo.
Tenemos la siguiente ecuación que está en forma general:
Como te he comentado anteriormente, el vector de dirección de una recta en forma general viene determinado en función de sus coeficientes A y B:
Por tanto, en nuestro caso A=2 y B=3, por lo que el vector de dirección de la recta es:
Ya tenemos el vector de dirección y sólo nos falta obtener un punto que pase por la recta.
Para calcular un punto que pase por la recta, debemos calcular cualquier punto que pertenezca a la recta.
¿Cómo sabemos que un punto pertenece a una recta?
Vamos a verlo.
Cómo saber si un punto pertenece a una recta
Sabemos que un punto pertenece a una recta sustituyendo las coordenadas del punto por las variables x e «y» de la recta. Si se cumple la igualdad, entonces el punto pertenece a la recta y no pertenecerá en caso contrario.
Por ejemplo, ¿pertenece el punto A (1,2) a la recta de nuestro ejemplo?
Para descubrirlo, sustituimos la x por 1 y la «y» por 2. Si se cumple la igualdad, entonces el punto pertenece a la recta.
Vamos a sustituir x e «y» de la recta por las coordenadas del punto:
Operamos y vemos que la igualdad no se cumple:
Por tanto, el punto A no pertenece a la recta.
Dicho esto, seguimos con nuestro ejercicio.
Habíamos calculado el vector de dirección y necesitamos calcular un punto que pertenezca a la recta.
Entonces, ¿cómo podemos calcular cualquier punto que pertenezca a la recta?
Calculamos cualquier punto que pertenezca a la recta dándole un valor cualquiera a x y resolviendo la ecuación con respecto de «y», encontrando con ello un valor que cumpla la igualdad para ese valor de x.
Por ejemplo, le vamos a dar el valor a x de x=1 (puedes darle cualquier valor):
Sustituimos la x por 1 en la ecuación de la recta:
Y despejamos la «y», cuyo valor es igual a:
Por tanto, las coordenadas del punto que pertenece a la recta son:
Ya tenemos el vector de dirección y un punto que pasa por la recta:
Con estos dos datos, ya podemos calcular la ecuación vectorial:
Las ecuaciones paramétricas:
Y la ecuación contínua:
Si quieres aprender el resto de ecuaciones de la recta, además de saber resolver todos los ejercicios sobre recta, te recomiendo el Curso de Geometría Analítica en el Plano, con explicaciones con todo detalle.
¿Necesitas ayuda con las matemáticas? ¿Quieres que te explique cualquier duda que te surja paso a paso?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: