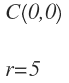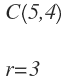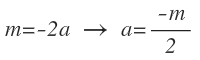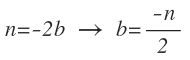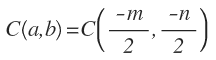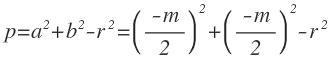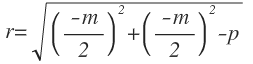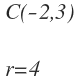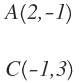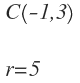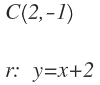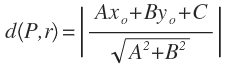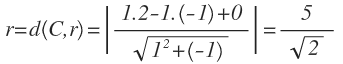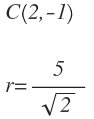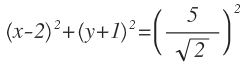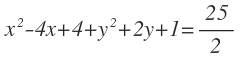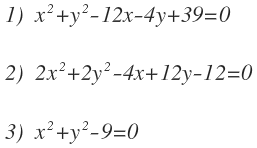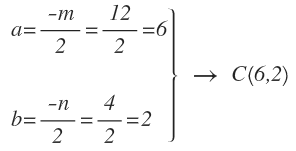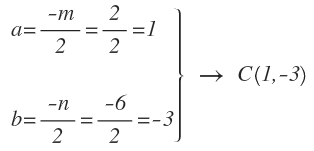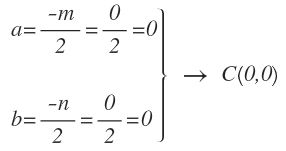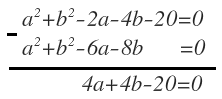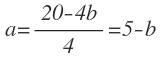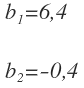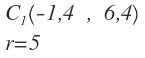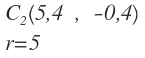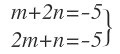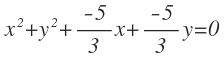A coninuación te voy a explicar cómo calcular la ecuación de la circunferencia. Veremos qué datos necesitamos para obtenerla, cómo se expresa esta ecuación y resolveremos ejercicios paso a paso aplicando lo aprendido.
¡Empezamos!
Si has llegado hasta aquí es porque quieres aprender a resolver algún ejercicio. ¿Has pensado en apuntarte a clases de matemáticas online?. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Aquí tienes un vídeo con ejercicios resueltos paso a paso:
Y aquí la explicación de todo lo que necesitas saber:
Ecuación de la circunferencia
La circunferencia es el conjunto de puntos del plano que equidistan de un punto fijo llamado centro.
Si tenemos una circunferencia de centro C(a,b) y de radio r y tomamos cualquier punto que pertenezca a la circunferencia:
El radio siempre va a ser la distancia entre el punto P de la circunferencia y el centro C:
Te recuerdo, que la fórmula para calcular la distancia entre dos puntos es la siguiente:
En nuestro caso, los dos puntos que tenemos son el punto P y el punto P:
Sustituimos las coordenadas de ambos puntos en la fórmula:
Pasando la raíz como cuadrado al segundo miembro nos queda:
Que es la ecuación de la circunferencia con centro en C(a,b) y de radio r.
Por tanto, para obtener la ecuación de la circunferencia, debemos conocer el centro y el radio y tan sólo debemos sustituir a y b por las coordenadas del centro y r por el valor del radio.
Por ejemplo, para obtener la ecuación de la circunferencia con centro en el origen y radio 5 sería, sustituimos en la fórmula anterior a y b por 0 y r por 5:
Operamos y nos queda:
La ecuación de la circunferencia con centro fuera del origen, por ejemplo con centro en C(5,4) y radio 3, la obtenemos sustituyendo «a» por 5, «b» por 4 y el radio por 3:
Podemos seguir operando en esta ecuación y obtendríamos la ecuación de la circunferencia en forma general, que es justo lo que veremos a continuación.
Ecuación de la circunferencia: forma general
Como acabamos de ver, si conocemos las coordenadas del centro de la circunferencia y su radio podemos llegar a esta expresión de la ecuación de la circunferencia:
Si desarrollamos los productos notables en el primer miembro nos queda:
Pasamos todos los términos al primer miembro y reordenamos términos para dejarlos de esta forma:
Si llamamos «m» al coeficiente que queda delante de la «x»:
Llamamos «n» al coeficiente que queda delante de la «y»:
Y llamamos «p» a los términos que no llevan «x» ni «y»:
Y los sustituimos en la expresión anterior, nos queda la siguiente fórmula:
Que corresponde a la ecuación de la circunferencia en su forma general.
En la forma general de la ecuación de la circunferencia, los términos elevados al cuadrado, es decir, x² e y², deben tener el mismo coeficiente, o lo que es lo mismo, el número que tengan delante debe ser el mismo. En caso contrario, no sería la ecuación de una circunferencia.
Para obtener el centro a partir de esta ecuación, debemos expresar las coordenadas del centro, a y b, en función de m y de n, que las obtenemos despejándolas a partir de las expresiones anteriores:
De esta manera, el centro lo podemos obtener como:
De la misma forma, si en la expresión de «p», sustituimos a y b por sus expresiones en función de m y n:
Podemos expresar el radio de la siguiente manera:
Aunque te parezca que las fórmulas son algo complicadas, verás que a la hora de aplicarlas para resolver ejercicios resulta mucho más sencillo.
Ejercicios resueltos sobre la ecuación de la circunferencia
Vamos a resolver unos cuantos ejercicios para aplicar todo lo aprendido sobre la ecuación de la circunferencia.
Ejercicio 1
Halla la ecuación de la circunferencia que tiene de centro el punto C(-2,3) y de radio r=4. ¿Pertenecen los puntos A(2,3), B(-4,3) y D(1,5) a la circunferencia?
En este caso tenemos el centro y el radio:
Por tanto, en la siguiente expresión:
Sustituimos las coordenadas del centro y el radio por sus valores:
Desarrollamos los productos notables y el cuadrado del segundo miembro:
Y reordenamos términos para obtener la ecuación de la circunferencia en su forma general:
Para saber si cada uno de los puntos pertenecen a la circunferencia, debemos sustituir las coordenadas de cada punto por x y por «y» y comprobar si se cumple la igualdad. Si se cumple, el punto pertenece a la circunferencia y en caso contrario, el punto no pertenece.
Para ver si el punto A(2,3) pertenece a la circunferencia, sustituimos x por 2 e «y» por 3:
Operamos en el primer miembro y vemos que efectivamente el resultado es 0, igual al del segundo miembro, por tanto el punto A sí pertenece a la circunferencia:
Comprobamos ahora el punto B(-4,3), sustituyendo x e «y» por las coordenadas del punto:
Al operar en el primer miembro, el resultado no es igual al del segundo miembro, luego el punto B no pertenece a la circunferencia:
Por último, hacemos lo mismo con el punto C(1,5):
El resultado del primer miembro no es igual a cero, por lo que el punto C tampoco pertenece a la circunferencia:
Ejercicio 2
Hallar la ecuación de la circunferencia que pasa por el punto A(2,-1) y cuyo centro es C(-1,3).
En este ejercicio conocemos el centro y un punto de la circunferencia:
Nos falta conocer el radio de la circunferencia para poder calcular su ecuación, que es igual a la distancia entre el punto A y el centro C:
Ahora ya conocemos el centro y el radio:
Por tanto, ya podemos calcular la ecuación de la circunferencia.
En la siguiente expresión:
Sustituimos a, b y r por sus valores:
Operamos:
Y reordenamos términos para dejar la ecuación en su forma general:
Ejercicio 3
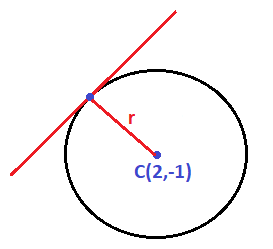
Hallar la ecuación de la circunferencia de centro C(2,-1) y que sea tangente a la recta r: y=x+2.
En este caso tenemos como datos el centro y una recta tangente a la circunferencia:
El radio será igual a la distancia entre el centro y la recta, ya que la recta tangente siempre es perpendicular al radio.
La fórmula para calcular la distancia de un punto a una recta es:
Para poder aplicarla, necesitamos poner la ecuación de la recta en su forma general:
Sustituimos los coeficientes de la ecuación de al recta y las coordenadas del centro en la ecuación, por lo que obtenemos el valor del radio:
Ya tenemos el valor del centro y del radio:
Sustituimos sus valores en la ecuación de la circunferencia:
Desarrollamos los cuadrados:
Pasamos el 2 multiplicando al primer miembro para eliminar el denominador:
Y reordenamos términos:
Observa como el coeficiente del término x² y del término y² es el mismo.
Ejercicio 4
Hallar el centro y el radio de las siguientes circunferencias:
Vamos a calcular el centro y el radio a partir de la ecuación general de una circunferencia:
Para ello hay que obtener a y b en función de m y n:
Las expresiones del centro y del radio serán:
Vamos con la primera circunferencia:
Calculamos los valores de a y b y obtenemos directamente el centro:
El radio lo calculamos a partir de esta fórmula:
Sustituimos a, b y p por sus valores y operamos:
Seguimos con la segunda circunferencia:
En primer lugar simplificamos la expresión para que delante de los términos al cuadrado tengamos un 1, tal y como es la forma general de la ecuación de una circunferencia:
Calculamos a y b para obtener el centro:
Y calculamos el radio:
Y finalmente, la tercera circunferencia:
Calculamos el centro:
El valor del radio es:
Ecuación de la circunferencia que pasa por dos puntos
Vamos a resolver un ejercicio sobre la ecuación de la circunferencia que pasa por dos puntos:
Hallar la ecuación de la circunferencia que pasa por los puntos A(1,2) y B(3,4) y que tiene de radio r=5.
En este caso conocemos el radio, pero no conocemos el centro. En su lugar nos dan dos puntos que pertenecen a la circunferencia.
A partir de los dos puntos que pertenecen a la circunferencia debemos calcular las coordenadas del centro a y b. Para ello partimos de la ecuación de la circunferencia:
Sustituimos las coordenadas del punto A por x e y en la fórmula:
Desarrollamos los cuadrados:
Y reordenamos términos:
Sustituimos las coordenadas del punto B por x e y en la fórmula:
Desarrollamos los cuadrados:
Y reordenamos términos:
Restamos las dos ecuaciones obtenidas para eliminar los términos que están al cuadrado:
Y de la expresión obtenida despejamos a:
En la primera de las ecuaciones anteriores:
Sustituimos «a» por su expresión en función de «b»:
Desarrollamos el producto notable y eliminamos el paréntesis multiplicándolo por el -2:
Operamos y reordenamos términos:
Nos queda una ecuación de segundo grado completa, que la resolvemos y obtenemos las siguientes soluciones:
El primer valor de b, lo sustituimos en la expresión donde despejamos «a» y obtenemos su valor:
Con estos valores de a y b tenemos uno de los posibles centros de la circunferencia que cumple las condiciones del enunciado:
Del segundo valor de b, calculamos otro valor de «a»:
Obteniendo las coordenadas del otro centro que cumple las condiciones:
Con el primer centro y conociendo el radio, obtenemos la ecuación de la primera circunferencia:
Y con el segundo centro y el mismo valor del radio, obtenemos la ecuación de la segunda circunferencia:
Ecuación de la circunferencia que pasa por tres puntos
Vamos a ver cómo se resuelve un ejercicio sobre la calcular la ecuación de la circunferencia que pasa por tres puntos:
Hallar la ecuación de la circunferencia que pasa por los puntos A(1,2), B(2,1) y D(0,0).
En este ejercicio no conocemos ni el centro ni el radio de la circunferencia.
A partir de la ecuación de la circunferencia en su forma general:
Debemos encontrar los valores de m, n y p, a partir de los cuales obtendremos el centro y el radio. Para ello, como tenemos tres incógnitas, necesitamos tres ecuaciones, que las obtendremos sustituyendo las coordenadas de cada punto en la ecuación.
Sustituimos las coordenadas del punto A por x e y en la ecuación:
Sustituimos las coordenadas del punto B por x e y en la ecuación:
Y hacemos lo mismo con el punto C:
De la tercera ecuación despejamos el valor de p:
En la primera ecuación:
Despejamos el valor de p, operamos y reordenamos términos:
En la segunda ecuación:
Despejamos el valor de p, operamos y reordenamos términos:
Y con las dos primeras ecuaciones simplificadas, formamos un sistema de dos ecuaciones con dos incógnitas:
Cuya solución es:
Conocidos los valores de m, n y p, los sustituimos en la fórmula de la ecuación de la circunferencia en su forma general:
Y nos queda:
Finalmente eliminamos denominadores:
¿Necesitas ayuda con las matemáticas? ¿Quieres que te explique cualquier duda que te surja paso a paso?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: