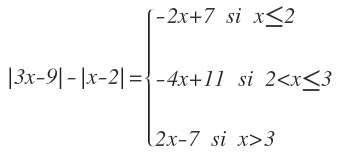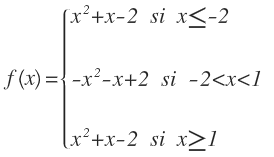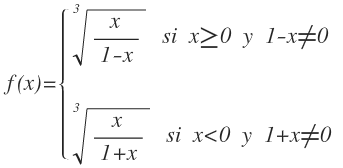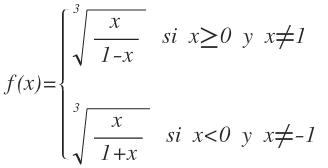A continuación te voy a explicar cómo transformar funciones con valor absoluto en funciones definidas a trozos, así como a obtener su dominio. Lo veremos con ejercicios resueltos paso a paso.
Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
¡Empezamos!
Valor absoluto de una función
Para entender las funciones con valor absoluto, antes debemos entender la definición de valor absoluto
Definición de valor absoluto en una función
Como ya sabes, el valor absoluto de un número es el valor positivo de ese número. Por ejemplo, el valor absoluto de -3 es igual a 3: |-3|=3.
El valor absoluto de una función corresponde a transformar los valores negativos de la función en positivos, por lo que la función es positiva en todo su dominio.
La definición de valor absoluto es la siguiente:
Todos los valores del valor absoluto de una función deben ser positivos. Para ello se trasforma la función con valor absoluto en una función definida a trozos, donde para un valor cualquiera x, si es mayor o igual a cero se toma el mismo valor x y si es menor que cero se toma el valor x multiplicado por -1, es decir -x.
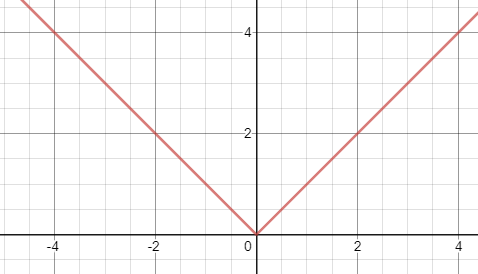
Si representamos el valor absoluto de x, nos queda:
Como ves, la gráfica siempre está por encima del eje x o lo que es lo mismo, siempre es positiva.
Para el primer tramo, representamos y=x para los valores de x mayores o iguales que cero, es decir, x sólo puede tomar valores que sean mayores o iguales que cero. En este caso, para cualquier valor de x, «y» tomará el mismo y además será siempre positivo (ya que no podemos darle valores negativos a la x)
Para el segundo tramo, representamos y=-x, para los valores de x menores que cero, es decir, que x sólo puede tomar valores que sean menores que cero. Ahora, si por ejemplo x=-1, «y» será igual a 1, ya que y=-(-1)=1. Por tanto, para cualquier valor negativo de x, «y» siempre será positiva.
En el Curso de Funciones tienes lecciones sobre cómo representar ecuaciones y funciones definidas a trozos.
Valor absoluto de una función
Si entre las barras de valor absoluto hay una función, para valores mayores o iguales que cero de la función se toma la misma función y para valores menores que cero de la función, la función se multiplica por -1
Ejercicios resueltos de funciones con valor absoluto
Para que te quede más claro, vamos a ir resolviendo ejercicios de funciones con valor absoluto aplicando lo que acabamos de ver.
Expresar las siguientes funciones con valor absoluto como funciones definidas a trozos. Calcular su dominio y representarlas
Ejercicio 1
Aplicamos la definición de valor absoluto para una función, dejando en el primer tramo la función tal y como está si la función es mayor o igual que cero y en el segundo tramo, la función multiplicada por -1, si la función es menor que cero:
Operamos en las desigualdades:
El dominio de la función es todo el conjunto de los números reales:
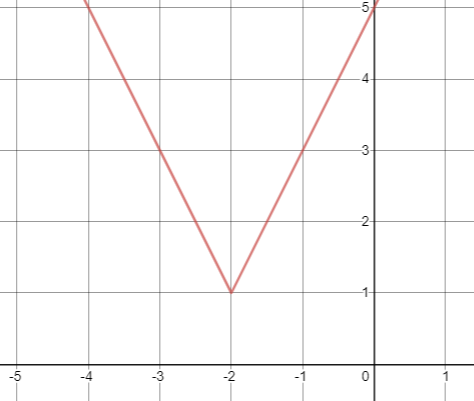
Si la representamos queda:
Ejercicio 2
En este caso, además del término con valor absoluto, la función tiene otro término sin función absoluto. En estos casos, aplicamos la fórmula de la definición de valor absoluto sólo en el término donde tenemos el valor absoluto, dejando el resto de la función igual.
En las desigualdades, se pone sólo lo que está encerrado entre las barras (cuidado con esto):
Ahora operamos tanto en cada tramo de la función como en las desigualdades:
El domino de la función es todo R:
Y la función representada queda de la siguiente manera:
Ejercicio 3
En esta función tenemos dos términos con valor absoluto. En estos casos, no es posible aplicar la definición de valor absoluto en los dos términos a la vez, por lo que tenemos que hacerlo por separado.
El primer término queda:
Operamos en las desigualdades:
El segundo término queda:
Operamos en las desigualdades:
Ya tenemos definidos cada uno de los términos en funciones definidas a trozos. Ahora lo que tenemos que hacer es unificarlo todo en una sola función. Para ello, representamos en la recta real los puntos donde la función cambia de tramo de cada término, que en nuestro caso es 2 y 3:
Ahora, escribimos el valor de la función para cada intervalo. El primer término |3x-9|, es igual a 3x-9 para valores de x mayores o iguales que 3 y es igual a -3x+9 para valores de x menores que 3. Como también tenemos el 2, los valores menores que 3 está divido en 2 intervalos, por lo que lo indicamos en cada intervalo:
En la misma recta, representamos el segundo término de la función |x-2|. Para valores de x mayores o iguales que 2, la función es igual a x-2. Lo indicamos en el intervalo de 2 a 3 y de 3 en adelante. Para valores de x menores que 2, la función es igual a -x+2. Nos queda:
Tenemos el valor de la función de cada término para cada intervalo. Ahora vamos a calcular un sólo valor de la función en cada intervalo, realizando la operación que nos marca la función (primer término menos el segundo término) pero con el valor que tiene cada uno de los términos en cada intervalo.
Para el primer intervalo desde menos infinito hasta 2:
Para el segundo intervalo desde 2 hasta 3:
Para el tercer intervalo desde 3 hasta infinito:
Indicamos el valor de la función en cada uno de los intervalos en la recta real para tenerlo más claro:
Y eso lo indicamos como una función definida a trozos. Los «iguales» en las desigualdades se pueden colocar en cualquier tramo, siempre que tengamos un solo «igual» para cada valor de x. Para el 2 lo coloco en el primer tramo y para el 3 en el segundo tramo:
Una vez ya tenemos la función definida a trozos, calculamos su dominio, que es todo R:
Y representamos la función:
Ejercicios resueltos de funciones de segundo grado con valor absoluto
Empezamos aplicando la definición de valor absoluto:
Ahora tenemos que resolver las inecuaciones de segundo grado que nos quedan en las condiciones:
Es decir, debemos saber los rangos de valores de x donde se cumplan que la función sea mayor o igual que cero o menor que cero.
Para ello, igualamos la inecuación a cero y la convertimos en una ecuación:
Resolvemos la ecuación de segundo grado resultante, cuyas soluciones son:
Representamos las soluciones en la recta numérica:
Nos ha quedado la recta dividida en tres tramos. Debemos saber en qué tramos la función es positiva o negativa.
Para saber si el tramo que está a la izquierda de -2 es positivo o negativo, le damos un valor a la x que esté a la izquierda de -2 en la recta, por ejemplo el -3 y vemos su resultado.
Cuando x=-3:
El resultado es 4, por lo que la función es positiva.
Para el tramo central, le damos un valor a la x que esté entre -2 y 1, por ejemplo el 0:
Para x=0:
El resultado es -2, por lo que la función es negativa.
Y para el tramo de la derecha le damos a la x un valor que quede a la derecha de 1. Por ejemplo el 2. Para x=2:
El resultado es mayor que cero, por lo que la función es positiva.
Si representamos en la recta los tramos positivos y negativos nos queda de la siguiente forma:
Ahora ya podemos resolver las inecuaciones de segundo grado.
Empezamos con la inecuación donde la función es mayor o igual que cero:
La función es positiva para los valores de x que sean menores o iguales que -2 y mayores o iguales que 1:
Por tanto, en estos rangos, la función toma este valor:
Resolvemos ahora la inecuación donde la función es menor que cero:
La función es negativa para los valores comprendidos entre -2 y 1:
En este rango, la función toma este valor:
El valor que toma la función es función de si es positiva o negativa lo sabemos de aplicar la definición de valor absoluto:
Si escribimos el valor de cada intervalo en la recta numérica nos queda:
Por último, escribimos la función como una función definida a trozos, que ya se puede representar en los ejes de coordenadas:
Ejercicios de funciones racionales con valor absoluto
Calcular el dominio de las siguientes funciones con valor absoluto
Ejercicio 1
En primer lugar, representamos la función como una función definida a trozos y para ello aplicamos la definición de valor absoluto sólo en el término afectado por valor absoluto, dejando el resto de la función igual.
En el primer tramos dejamos la x encerrada en valor absoluto como positiva cuando x es mayor o igual que cero. Además como nos queda una función racional, debemos tener en cuenta que el denominador no puede ser igual a cero, por lo que lo añadimos como condición.
En el segundo tramo dejamos la x encerrada en valor absoluto como negativa cuando x es menos que cero. Además, igual que antes, al tener una función racional, debemos tener en cuenta que el denominador no puede ser igual a cero, por lo que lo añadimos como condición.
En este caso, en cada tramo tenemos funciones irracionales de índice impar, por lo que existen siempre y por tanto no añaden ninguna condición a cada tramo.
La función nos queda de la siguiente forma:
Operamos en las condiciones de cada tramo para que quede en función de los valores de x:
El dominio del primer tramo es el siguiente:
Es decir, existe desde 0 (incluido) hasta 1 (sin incluir) y desde 1 (sin incluir) hasta infinito.
El dominio del segundo tramo es el siguiente:
Es decir, existe desde menos infinito hasta -1 (sin incluir) y desde -1 (sin incluir) hasta 0 (sin incluir).
Por tanto, considerando la función entera, existe en todo el conjunto de los números reales, menos en x=-1 y x=1:
Ejercicio 2
Aplicamos la definición de valor absoluto para escribir la función como una función definida a trozos. Además, en cada tramo, al tener una función racional, añadimos la condición de que el denominador no puede ser igual a cero:
Ahora vamos a obtener las condiciones en función de valor de x.
La desigualdad del primer tramo es:
Tenemos una inecuación racional que debemos resolver. En esta lección tienes explicado cómo resolver inecuaciones racionales más paso a paso: Cómo resolver inecuaciones racionales.
Igualamos el denominador a cero:
Resolvemos la ecuación, obteniendo como resultado x=2. Lo representamos en la recta real, como un punto vacío, ya que al estar en el denominador nunca se toma:
Ahora vamos a obtener el signo de cada intervalo.
Para saber el signo del tramo que queda a la izquierda de 2, le damos a x el valor de 0 en la función y operamos:
Para saber el signo del tramo que queda a la derecha de 2, le damos a x el valor de 3 en la función y operamos:
Representamos el signo de cada intervalo:
Estamos buscando los valores de x que hacen la función positiva, luego el tramo que buscamos es desde 2 hasta infinito, o lo que es lo mismo, los valores que sean mayores que 2 (el 2 no se toma ya que hace el denominador igual a cero y por tanto no pertenece al dominio):
Ahora vamos a ver qué valores de x hacen que la función racional de la condición del segundo tramo sea menor que cero.
La inecuación es la misma que antes luego ya tenemos el signo de cada intervalo:
Ahora los valores de x que buscamos son los que hacen que la función sea negativa, es decir, desde menos infinito hasta 2 (sin incluir) o lo que es lo mismo, los valores de x menores que 2:
Por tanto, la función queda de la siguiente forma:
La función existe en todo el conjunto de los números reales menos en x=2, luego el dominio es:
¿Necesitas ayuda en matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: