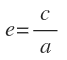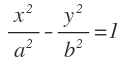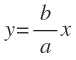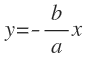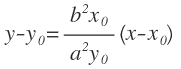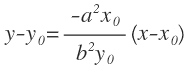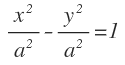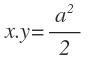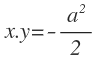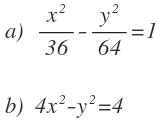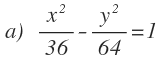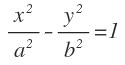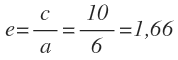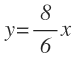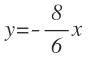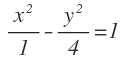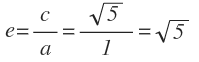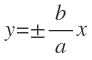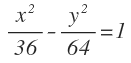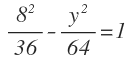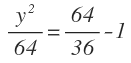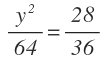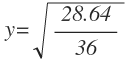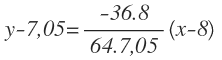A continuación vamos a ver qué es una hipérbola. Te explicaré cuáles son sus elementos más importantes, la ecuación de una hipérbola, su excentricidad, las ecuaciones de sus asíntotas y aprenderás también a calcular la recta tangente y la recta normal a un punto de la hipérbola. Con ejercicios resueltos paso a paso.
¡Vamos allá!
Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Qué es una hipérbola
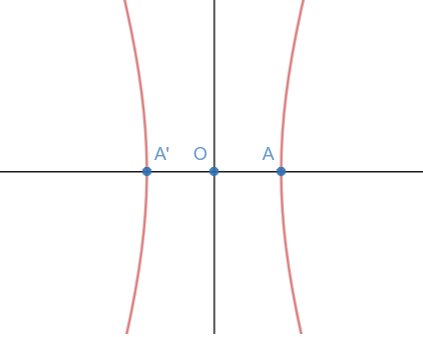
Una hipérbola es el lugar geométrico de todos los puntos del plano, cuya diferencia de distancias (en valor absoluto) a dos puntos fijos llamados focos, es constante e igual a 2a (siendo 2a la longitud del eje real de la hipérbola).
Es decir, en una hipérbola:
La distancia del punto P al punto F’, menos la distancia del punto P al punto F es igual a la longitud del eje mayor, que mide 2a:
Elementos de la hipérbola
Los elementos de la hipérbola son los siguientes:
- Focos: Son los puntos fijos F y F’
- Radio vectores: Son los segmentos PF’ y PF
- Centro de la hipérbola: Punto O donde se cortan los ejes
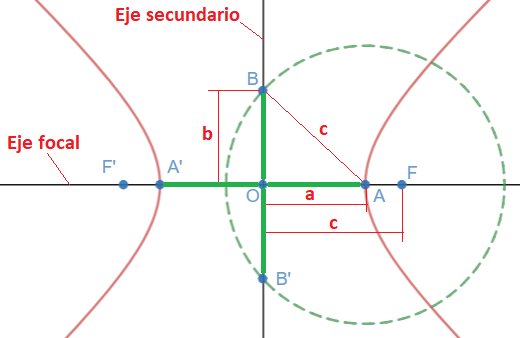
- Vértices: Son los puntos A, A’, B y B’. A y A’
- A y A’ son los puntos de corte del eje real con la hipérbola. Sus coordenadas son (a,0) y (-a,0) respectivamente.
- B y B’ son los puntos de corte del eje secundario con la circunferencia de centro en el punto A y radio «c». Sus coordenadas son (b,0 ) y (-b,0) respectivamente.
- Eje real: Es el segmento AA’, cuya longitud es 2a
- Eje imaginario: Es el segmento BB’, cuya longitud es 2b
- Distancia focal: Es el segmento FF’, cuya longitud es 2c
- Semieje real: Es la longitud «a»
- Semieje imaginario: Es la longitud «b»
- Semidistancia focal: Es la longitud «c»
- Eje focal: Es la recta que pasa por los focos y por el eje real
- Eje secundario: Es la mediatriz del segmento FF’
Relación entre las longitudes a, b y c de la hipérbola
Las longitudes de los semiejes, a y b, están relacionadas con la semidistancia focal, c, están relacionadas entre sí.
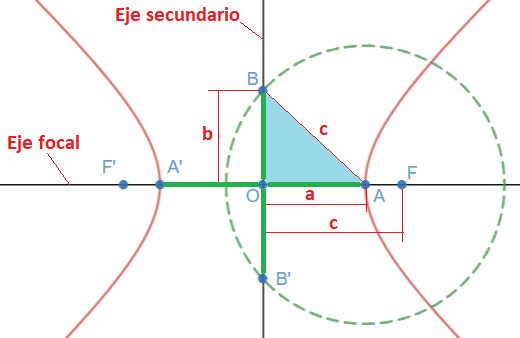
Como hemos visto en los elementos de la hipérbola, los puntos B y B’ son los puntos de corte del eje secundario con la circunferencia de centro en el punto A y radio «c», por tanto, el segmento que une el punto A con el punto B es igual a c, que corresponde con el radio de la circunferencia.
Entre los puntos O, A y B se forma un triángulo rectángulo, cuyos catetos son «a» y «b» y su hipotenusa es «c»:
Así que, las distancias «a», «b» y «c» están relacionadas por el teorema de Pitágoras:
Excentricidad de la hipérbola
Las ramas de las hipérbolas pueden ser más abiertas o más cerradas. Esta característica se mide mediante la excentricidad de la hipérbola, que es el cociente entre la entre la semidistancia focal «c» y el semieje real «a»:
La excentricidad es un número mayor que 1.
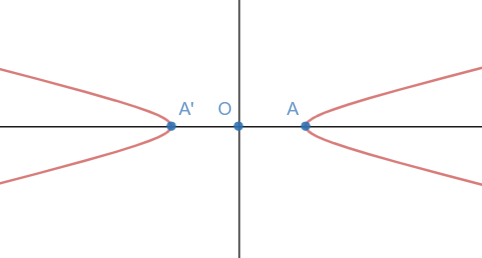
Para un mismo valor de «a», cuanto más se aproxima la excentricidad a 1, las ramas de la hipérbola son más cerradas:
Por el contrario, cuanto mayor es el valor de la excentricidad, las ramas de la hipérbola son más abiertas:
Ecuación de la hipérbola con centro en el origen
La ecuación de la hipérbola con centro en el origen se obtiene a partir de calcular la distancia de un punto cualquiera a los focos, lo cual no voy a demostrar aquí. Operando y reordenando términos se llega a la siguiente expresión que se corresponde con la ecuación de la hipérbola:
Donde «a» es la longitud del semieje real y «b» es la longitud del semieje imaginario. El centro de la hipérbola se encuentra en el origen de coordenadas (0,0).
Asíntotas de la hipérbola
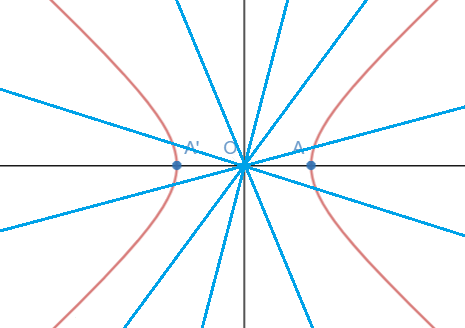
En una hipébola, podemos trazar infinitas rectas que pasen por el origen. Unas cortarán a la hipérbola en dos puntos y otras no cortarán a la hipérbola:
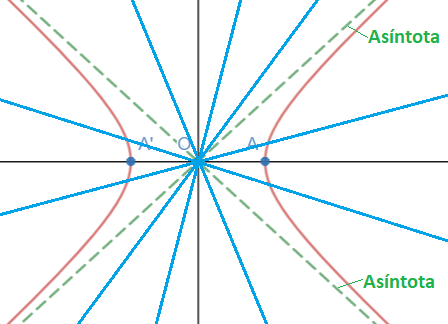
Las rectas que más se acercan a la hipérbola pero no llegan nunca a tocarla son las asíntotas de una hipérbola. Una hipérbola tiene dos asíntotas:
Ecuaciones de las asíntotas de una hipérbola
Las ecuaciones de las asíntotas de una hipérbola son:
Donde «a» es la longitud del semieje real y «b» es la longitud del semieje imaginario.
Ecuación de la recta tangente y de la recta normal a la hipérbola en un punto
Vamos a ver ahora cómo calcular la ecuación de la recta tangente a la hipérbola en un punto, así como la ecuación de la recta normal.
Ecuación de la recta tangente a la hipéborla
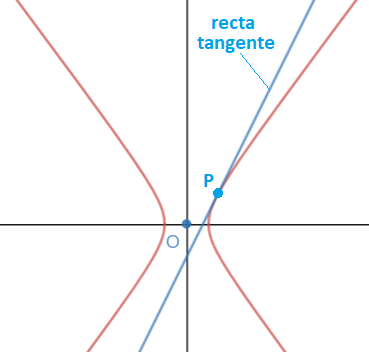
La recta tangente a una hipérbola es aquella que toca a la curva de la hipérbola en un punto:
La ecuación de la recta tangente a una hipérbola en un punto es la siguiente:
Donde X0 e Y0 son las coordenadas del punto, «a» es la longitud del semieje real y «b» la longitud del semieje imaginario.
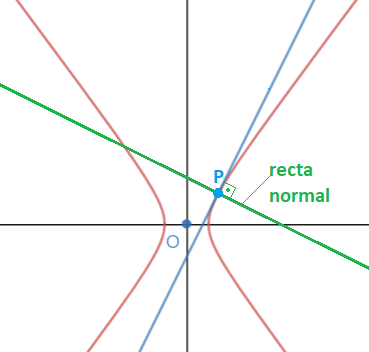
Ecuación de la recta normal a la hipérbola en un punto
La recta normal a la hipérbola es un punto es la recta perpendicular a la recta tangente y que pasa por el punto P:
La ecuación de la recta normal a la hipérbola en un punto es:
Donde X0 e Y0 son las coordenadas del punto, «a» es la longitud del semieje real y «b» la longitud del semieje imaginario.
Hipérbola equilátera
Una hipérbola equilátera es aquella donde la longitud del eje real y la del eje imaginario son iguales:
Obteniendo denominador común y después pasando el denominador al segundo miembro, la ecuación de la hipérbola equilátera queda:
Las asíntotas de la hipérbola equilátera son:
Y su excentricidad:
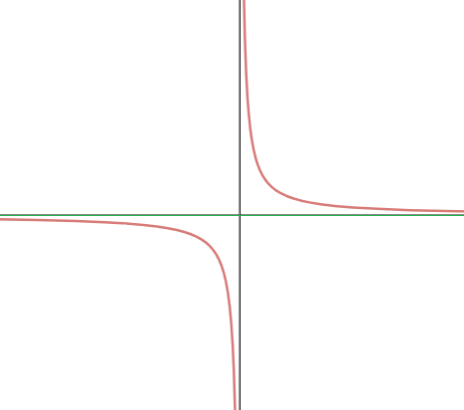
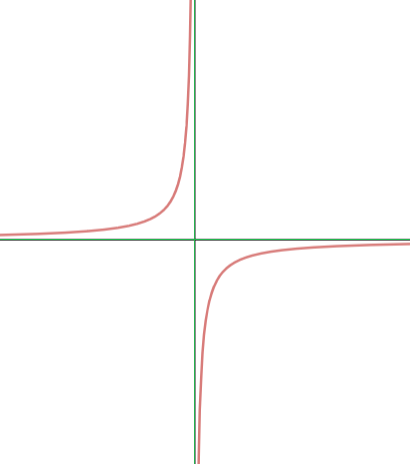
Si giramos la hipérbola equilátera 45 grados a la izquieda, las asíntotas pasan a ocupar el lugar de los ejes de coordenadas:
En este caso, la ecuación de la hipérbola equilátera queda de la siguiente manera:
Si la giramos 45 grados a la derecha (-45º), entonces la gráfica de la hipérbola es:
Y la ecuación en este caso es:
Ejercicios resueltos sobre la hipérbola
Ejercicio 1
Halla las coordenadas de los focos, las longitudes de los semiejes, las coordenadas de los vértices, la excentricidad y las asíntotas de las siguientes hipérbolas:
Empezamos con la primera hipérbola:
La ecuación de una hipérbola es:
Luego a partir del denominador de la primera fracción calculamos el valor de «a»:
Con el valor de «a», obtenemos las coordenadas de los vértices A y A’:
Del denominador de la segunda fracción obtenemos el valor de «b»:
Conocido el valor de «b», las coordenadas de B y B’ son:
La relación entre «a», «b» y «c» es:
Sustituimos «a» y «b» por su valor, despejamos «c» y operamos:
Con el valor de «c», obtenemos las coordenadas de los focos:
Calculamos la excentricidad, como el cociente de «c» entre «a»:
Finalmente, calculamos las ecuaciones de las asíntotas, a partir de los valores «a» y «b»:
Seguimos con la segunda elipse:
En primer lugar, debemos poner la ecuación de la misma forma que la ecuación de una hipérbola:
Para ello, dividimos todos los términos de la ecuación entre 4, para conseguir que en el segundo miembro nos quede un 1:
Simplificamos fracciones:
A partir del denominador del primer término hallamos el valor de «a» y las coordenadas de A y A’:
Con el denominador del segundo término, obtenemos el valor de «b» y las coordenadas de B y B’:
Con la relación entre «a», «b» y «c», despejamos «c» y calculamos su valor:
Con el valor de «c», obtenemos las coordenadas de los focos:
La excentricidad en este caso es:
Y finalmente, obtenemos las ecuaciones de sus asíntotas:
Ejercicio 2
Halla las ecuaciones de la rectas tangente y normal a la siguiente hipérbola en el punto de abcisa x=8 y considerando que el punto se encuentra en el primer cuadrante:
Empezamos obteniendo las coordenadas del punto. Para ello sustituimos x por 8 en la ecuación de la elipse:
Y ahora despejamos el valor de «y»:
Nos quedan dos soluciones de «y». Como el enunciado nos dice que el punto está en el primer cuadrante, nos quedamos sólo con el valor positivo, por lo que las coordenadas del punto son:
La fórmula de la ecuación de la recta tangente a un hipérbola es:
Sustituimos X0 e Y0 por las coordenadas del punto y «a²» y «b²» por sus valores:
Operamos y nos queda:
Calculamos ahora la ecuación de la recta normal, cuya ecuación es:
Sustituimos X0 e Y0 por las coordenadas del punto y «a²» y «b²» por sus valores:
Operamos y nos queda:
¿Necesitas ayuda con las matemáticas? ¿Quieres que te explique cualquier duda que te surja paso a paso?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: