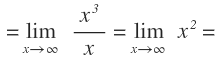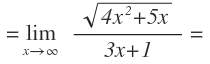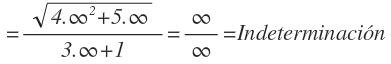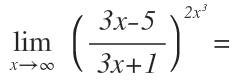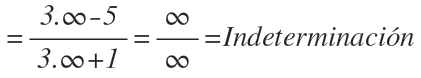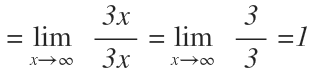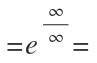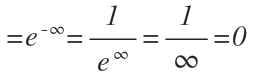A continuación te voy a explicar cómo calcular límites con indeterminaciones cero por infinito, infinito menos infinito y 1 elevado a infinito. Lo veremos al detalle mientras que con ejercicios resueltos paso por paso.
Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
La resolución de estas indeterminaciones se encadenan con otros tipos de indeterminaciones como infinito entre infinito, por lo que debes saber resolver también esa indeterminación (la tienes explicada en el Curso de Límites, junto con todas las indeterminaciones).
Cálculo de límites con indeterminación cero por infinito
Cualquier número multiplicado por cero es cero, pero a su vez, cualquier número multiplicado por infinito es infinito. Entonces ¿Cuanto es cero por infinito? ¿Es cero? ¿Es infinito?
Pues ni es una cosa ni es otra. Por eso mismo, cero por infinito es otra indeterminación
El procedimiento para resolver límites con indeterminación cero por infinito es:
- Llegar a la indeterminación cero por infinito sustituyendo la x por el número al que tienda
- Operar dentro de la función para eliminar la indeterminación
- Resolver la indeterminación infinito entre infinito que nos queda
Vamos a resolver un ejemplo de límite con indeterminación cero por infinito:
En primer lugar, sustituimos la x por infinito y llegamos a la conclusión que estamos ante una indeterminación cero por infinito:
Para resolver las indeterminaciones cero por infinito, lo que hay que hacer antes de nada es operar dentro del límite. En este caso, podemos multiplica la fracción por el paréntesis y queda:
Volvemos a sustituir la x por infinito y llegamos a otra indeterminación, esta vez de infinito entre infinito:
Para resolver las indeterminaciones infinito entre infinito, nos quedamos en el numerador y en el denominador con el término de mayor grado y después operamos:
Sustituimos la x por infinito y llegamos a la solución final del límite, que es infinito:
Vamos a resolver otro ejercicio de límite con este tipo de indeterminación.
Empezamos sustituyendo la x por infinito y llegamos a que tiene una indeterminación cero por infinito:
Operamos en la función multiplicando la fracción por la raíz y queda:
Sustituimos la x por infinito y llegamos al resultado de la indeterminación infinito entre infinito:
Nos quedamos con los términos de mayor grado del numerador y del denominador y resolvemos la raíz que nos queda en el numerador:
Podemos eliminar la x de ambas partes de la fracción y por tanto, llegamos al resultado final:
Cálculo de límites con indeterminación infinito menos infinito
Déjame hacerte una pregunta: ¿Infinito menos infinito es cero?
Mucha gente diría que si, pero la realidad es que no. Aunque sea un concepto abstracto, hay muchos «tamaños» de infinito, pero es no lo sabemos. Como no sabemos si los infinitos son iguales, infinito menos infinito es otra indeterminación:
Veamos un ejemplo:
Primero sustituimos la x por 1. Tenemos dos fracciones, que al sustituir resulta un número entre cero, cuyo resultado es infinito, luego estamos ante una determinación infinito menos infinito:
A partir de este punto, para resolver las indeterminaciones del tipo infinito menos infinito, seguiremos el siguiente procedimiento:
- Operamos con el fin de que nos quede un sólo término
- Descomponemos en factores los polinomios del numerador y del denominador.
- Eliminamos los factores que se repitan en el numerador y en el denominador. De esta forma se elimina la indeterminación
- Se vuelve a sustituir la x por el número al que tienda el límite, llegando a una solución determinada.
Para resolver este tipo de límites, debes tener muy claro cómo restar fracciones algebraicas, que lo tienes explicado en el Curso de Fracciones Algebraicas, así cómo descomponer polinomios, que lo tienes explicado en el Curso de Polinomios.
Seguimos resolviendo el límite del ejemplo con el procedimiento descrito. Restamos las fracciones algebraicas:
Multiplicamos paréntesis en el numerador. Como el segundo término tiene un signo menos delante, dejamos entre paréntesis el resultado de la multiplicación:
Eliminamos el paréntesis del numerador, cambiado de signo los términos de su interior:
Agrupamos términos y reordenamos:
Nos ha quedado un polinomio de tercer grado que tenemos que descomponer. Este tipo de polinomios se descomponen por Ruffini:
Eliminamos el factor que se repite en el numerador y en el denominador:
Volvemos a sustituir la x por 1, que al ser por la derecha, nos queda un cero positivo, por lo que el resultado es infinito:
Cálculo de límites con indeterminación infinito menos infinito con raíces
El procedimiento para resolver límites con la indeterminación infinito menos infinito con raíces es el siguiente:
- Llegar a la indeterminación infinito menos infinito sustituyendo la x por el número al que tienda
- Multiplicar y dividir por el conjugado de la función
- Operar en el numerador de la fracción resultante para simplificar términos
- Resolver la indeterminación infinito entre infinito que nos queda
Vamos a resolver un ejemplo de límite con indeterminación infinito menos infinito más despacio:
En primer lugar, sustituimos la x por infinito, lo que nos hacer llegar a la indeterminación infinito menos infinito:
Para resolver los límites con indeterminación infinito menos infinito hay que multiplicar y dividir por el conjugado de la función:
Operamos en el numerador de la fracción, donde nos queda una diferencia de cuadrados, ya que teníamos una multiplicación de suma por diferencia:
Resolvemos los cuadrados y agrupamos términos semejantes en el numerador:
Sustituimos la x por infinito. Llegamos a otra indeterminación, que ahora es la de infinito entre infinito:
Nos quedamos con el término de mayor grado tanto en el numerador como en el denominador, resolvemos la raíz en y agrupamos términos en el denominador:
Finalmente, eliminamos la x y llegamos al resultado del límite:
Cálculo de límites con indeterminación 1 elevado a infinito
Si te preguntara cuánto es 1 elevado a infinito ¿dirías que el resultado es 1? Pues no estarías en lo cierto, ya que 1 elevado a infinito se trata de otra indeterminación:
Para calcular los límites con indeterminación 1 elevado a infinito se calcula mediante esta fórmula:
Donde el número al que tiende la x puede ser cualquier número o puede ser más o menos infinito:
Seguiremos el siguiente procedimiento para resolver límites con la indeterminación 1 elevado a infinito:
- Llegar a la indeterminación 1 elevado a infinito la x por el número al que tienda
- Resolver, si es necesario, la indeterminación infinito entre infinito del límite de la función que forma la base de la potencia, para demostrar que su resultado es 1
- Aplicar la fórmula para resolver indeterminaciones 1 elevado a infinito
- Realizar operaciones en la función, dentro del límite
- Resolver la indeterminación infinito entre infinito que nos queda
Vamos a resolver paso a paso un ejemplo de límite con indeterminación 1 elevado a infinito:
Empezamos a resolver este límite sustituyendo la x por infinito y llegamos a este resultado:
Esta indeterminación no es 1 elevado a infinito, pero para poder aplicar la fórmula anterior, debemos demostrar el infinito entre infinito que está entre paréntesis es igual a 1.
Para ello resolvemos el límite de la función que forma la base de la potencia, es decir:
Sustituimos la x por infinito y llegamos a la indeterminación infinito entre infinito:
Nos quedamos con el mayor término del numerador y del denominador y operamos, llegando al resultado, que es igual a 1:
Sabiendo que el límite de la función, que forma la base de al potencia, cuando x tiende a infinito es 1, ahora sí podemos poner que este límite da como resultado la indeterminación 1 elevado a infinito:
Por tanto, aplicamos la fórmula anterior y nos queda:
Una vez aplicada la fórmula, tenemos que hacer operaciones. En primer lugar, dentro del paréntesis, realizamos la resta reduciendo a denominador común y agrupamos términos en el numerador:
Ahora eliminamos el paréntesis multiplicando por el término que tiene delante:
Cuando ya no podemos seguir operando, sustituimos la x por infinito y llegamos a la indeterminación infinito entre infinito:
Para resolver esta indeterminación, dejamos el término de mayor grado y operamos:
Finalmente, volvemos a sustituir la x por infinito, que nos queda «e» elevado a menos infinito, que por propiedades de las potencias, baja el denominador. «e» elevado a infinito es igual a infinito y 1 partido por infinito es igual a cero:
Cálculo de límites con infinito elevado a infinito
Vamos a ver cómo resolver los límites en los que una vez sustituyas la x por infinito, tengas como resultado infinito elevado a infinito.
Para empezar, infinito elevado a infinito no es una indeterminación. Infinito elevado a infinito es igual a infinito:
Por tanto, para resolver este tipo de límites, tan sólo tenemos que sustituir la x por infinito y el resultado se obtiene directamente.
Por ejemplo:
Sustituimos la x por infinito, que nos queda infinito elevado a infinito, cuyo resultado es infinito:
¿Necesitas ayuda con las matemáticas? ¿Quieres que te explique cualquier duda que te surja paso a paso?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: