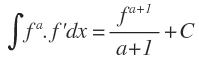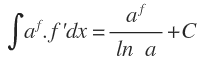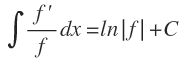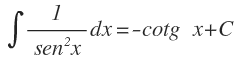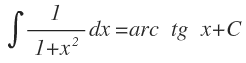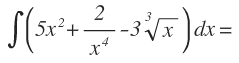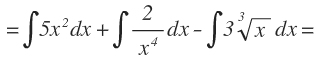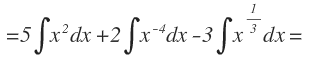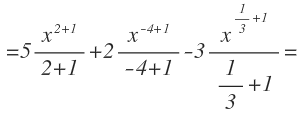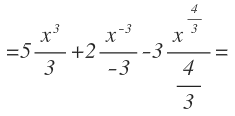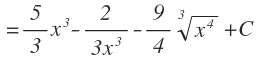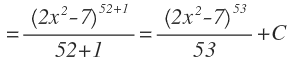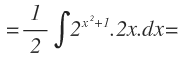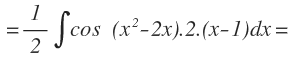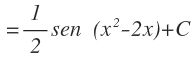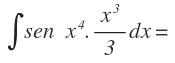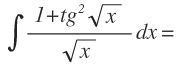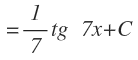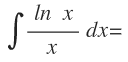Integrales inmediatas. Ejercicios resueltos de integrales inmediatas

A continuación te voy a explicar cómo aplicar las integrales inmediatas para resolver integrales, al mismo tiempo que utilizamos las propiedades de las integrales.

Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.

Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:

QUIERO APROBAR MATEMÁTICAS

Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.

Y si quieres aprender a resolver integrales de todo tipo, no sólo integrales inmediatas, en el Curso de Integrales Indefinidas, tienes explicados paso a paso todos los métodos de integración, con ejercicios resueltos y propuestos con la solución para practicar. Además me puedes preguntar todas las dudas que te surjan.

Vamos a empezar por tanto indicando cada una de las integrales inmediatas.

¿Qué son las integrales inmediatas?

Son integrales que se resuelven de una forma directa, aplicando su fórmula correspondiente. Para poder aplicar el método de integrales inmediatas, hay que transformar la función a integrar, mediante las propiedades de las integrales, para que quede de la misma forma que figura en cada una de las fórmulas.

Las funciones a integrar pueden ser de dos tipos:

• Funciones simples: Donde sólo interviene una x
• Funciones compuestas: Donde en lugar de la x de las funciones simples, aparece una función y  la multiplicación por su derivada.

Integrales inmediatas de funciones simples y compuestas

A continuación te dejo todas las integrales inmediatas de funciones simples, es decir, en aquellas que aparece sólo la x. La aplicación de este tipo de integrales se realiza directamente si tiene la misma forma que en cada fórmula.

Para que tenga la misma forma que en la fórmula, hay que aplicar las propiedades de las integrales (veremos cómo más abajo cuando resolvamos alguna integrales).

Las funciones compuestas son aquellas tienen la misma forma que las funciones simples, pero en lugar de aparecer una x, aparece una función con más de un término y la multiplicación por su derivada.

Para aplicar estas integrales inmediatas, es muy importante identificar que la derivada de la función existe o que se puede llegar hasta ella transformando la función utilizando las propiedades de las potencias.

Te dejo aquí las integrales inmediatas de funciones simples y compuestas:

Integral inmediata de una función potencial

Donde «a» tiene que ser distinto de -1.

Integral inmediata de una función exponencial

Integral inmediata de una función logarítmica

Integral inmediata de la función seno

Integral inmediata de la función coseno

Integral inmediata de la función tangente

Integral inmediata de una función cotangente

Integral inmediata de una función arco seno

Integral inmediata de una función arco tangente

Tabla de integrales inmediatas

Aquí te dejo una tabla de integrales inmediatas para que las tengas todas más a mano:

>> Descargar tabla de integrales inmediatas

Ejercicios resueltos de integrales inmediatas

¿Qué integrales se puede resolver con integrales inmediatas?

Pues todas aquellas que sea posible transformarlas mediante las propiedades de las integrales, para que queden igual que las fórmulas de las integrales inmediatas

La mejor forma de aprender a utilizar tanto las integrales inmediatas de funciones simples como las integrales inmediatas de funciones compuestas es practicando.

Por eso, vamos a resolver unas cuantas integrales donde nos encontraremos con todos los casos posibles y te iré indicando cómo solventar todos los problemas que te surjan, al mismo tiempo que vamos aplicando las propiedades de las integrales.

Ejercicio resuelto 1

En primer lugar separamos cada término de la función en una nueva integral, aplicando una de las propiedades de las integrales:

Ahora en cada integral, sacamos fuera las constantes:

Cada una de las integrales que nos ha quedado, aunque no lo parezca, se resuelven con la integral inmediata de la función potencial simple, ya que las funciones son de la forma de x elevada a un número:

A la primera integral no hay que hacerle nada, pero a la segunda y la tercera integral, debemos transformarlas para que estén de la misma manera. En la segunda integral, subimos la potencia al numerador y le cambiamos el signo y en la tercera, ponemos la raíz en su forma exponencial:

Ahora ya podemos aplicar la fórmula de la integral inmediata en cada una de las integrales:

Ya hemos integrado. Ahora vamos operar. Realizamos las sumas que nos han quedado en los exponentes y denominadores:

Y finalmente multiplicamos los números que nos han quedado, dejamos todos los exponentes como positivos o los volvemos a pasar a raíz y le añadimos la constante:

Ejercicio resuelto 2

Esta integral se resuelve con la integral inmediata de la función potencial compuesta:

Sabemos que se utiliza esta porque vemos una función elevada a un exponente.

La función es la que está elevada al exponente, que en este caso es:

Y su derivada por tanto es:

Ambas funciones están en la integral, de la misma forma que están en la fórmula, por lo que la podemos aplicar sin necesidad de transformar nada.

La aplicamos, operamos y le añadimos la constante:

Ejercicio resuelto 3

Tenemos una integral de una función exponencial compuesta, que se resuelve con esta integral inmediata:

La función es la que está elevando al número e:

Y su derivada es:

Esta vez, la derivada no aparece en la integral

¿Entonces qué hacemos? ¿Ya no se puede seguir?

Sí que se puede seguir. Se puede arreglar. En este caso nos falta el 3 que corresponde a la derivada de la función. Al ser una constante podemos añadirla (multiplicando a todo lo demás), siempre y cuando también dividamos toda la integral por la misma constante.

Es decir, multiplicamos y dividimos por 3 para no alterar el resultado de la integral:

Ahora ya tenemos la función y su derivada, por lo que podemos aplicar la fórmula de la integral inmediata y queda:

Ejercicio resuelto 4

Esta integral la resolvemos con la fórmula de la integral inmediata de la función exponencial compuesta, ya que el 2 está elevado a una función que es:

La derivada de esta función es:

Que no aparece como tal en la integral, ya que le falta un 2. Al ser una constante, multiplicamos y dividimos por 2, para no alterar el resultado de la integral:

Y ahora ya podemos aplicar la fórmula de la integral inmediata:

Ejercicio resuelto 5

Esta integral se resuelve con la fórmula de la integral inmediata logarítmica compuesta, ya que tenemos un cociente de funciones. Según esta fórmula, la función está en el denominador, que es:

La derivada de la función es:

No aparece como tal en la integral pero podemos transformarla para que aparezca. En primer lugar sacamos fuera el 5:

Y ahora, le añadimos el 12 que necesitamos, dividiendo entre 12 también toda la integral, evidentemente:

Finalmente aplicamos la fórmula de la integral inmediata:

Ejercicio resuelto 6

Para resolver esta integral utilizaremos la fórmula de la integral inmediata  de la función seno compuesta.

La función que está dentro del coseno es:

Y su derivada:

Una vez más, no tenemos todos los factores de la derivada. Si te das cuenta, he descompuesto la derivada sacando factor común al 2, para que se viera más claramente el factor (x-1). Por tanto, nos falta un 2, por lo que se lo añadimos y dividimos la integral entre 2:

Ahora aplicamos al fórmula de la integral inmediata del seno:

Ejercicio resuelto 7

Esta integral la resolveremos con la fórmula de la integral inmediata del coseno compuesta, ya que dentro del seno hay una función, que está multiplicando a otra función que podría ser su derivada. Vamos a verlo.

Esta es la función que está dentro del seno:

Y su derivada es:

Que no aparece en la integral. Para que apareciera, le sobra el 3 que divide a x³ y le falta un 4. Por tanto, primero sacamos el 3 fuera de la integral:

Y ahora multiplicamos  y dividimos entre 4:

Ahora ya podemos aplicar la fórmula de la integral inmediata y sumarle la constante:

Ejercicio resuelto 8

Esta integral a simple vista no tiene forma de ninguna integral inmediata, pero se le parece mucho a la fórmula de la integral inmediata de la tangente compuesta:

La función que está dentro de la tangente es:

Y su derivada:

He desarrollado su derivad hasta dejar la x en forma de raíz. Así se ve más claro que en la integral, podemos obtener esta derivada añadiendo un 2 en el denominador. Por tanto, como se lo añadimos al denominador, es decir, está dividiendo, multiplicamos la integral por 2:

Y finalmente aplicamos la fórmula de la integral inmediata de la tangente:

Ejercicio resuelto 9

Esta integral se ve claramente que se resuelve con la otra fórmula de la integral inmediata de la tangente, donde la función es:

Y su derivada:

Que debería aparecer en el numerador pero no aparece, por lo que lo añadimos y dividimos entre 7:

Para en el último paso aplicar la fórmula de la integral inmediata y añadirle la constante:

Ejercicio resuelto 10

Esta integral, si te das cuenta, a priori,no tiene forma de ninguna de las integrales inmediatas. Sin embargo, se ve claramente que tenemos una función (sen x), que está multiplicada por su derivada (cos x).

Es decir tenemos una función elevada al cuadrado que es:

Cuya derivada es:

Ahora se ve más claro que podemos aplicar la fórmula de la integral inmediata de la función potencial compuesta, donde tenemos una función elevada a un número, multiplicada por su derivada:

Por tanto, aplicando esta fórmula y operando llegamos al resultado de la integral:

Ejercicio resuelto 11

Esta integral, es un caso similar al anterior, ya que tampoco se le parece directamente a ninguna de las fórmula de las integrales inmediatas.

Sin embargo, tenemos una función que es ln x y también tenemos su derivada, que es 1/x:

Es decir, volvemos a tener una multiplicación de una función por su derivada, por lo que otra vez tenemos que aplicar la fórmula de la integral inmediata de la función potencial compuesta:

donde en esta ocasión, la función está elevada a 1.

Por tanto, al aplicar la fórmula de esta integral inmediata y operar queda:

Como ves, para saber qué fórmula de integral inmediata hay que utilizar en cada caso, tienes que fijarte a cuál de ellas se parece la integral a resolver y si dentro de la integral tienes una función y su derivada o en el peor de los casos, si no tienes la derivada, si la puedes obtener añadiendo o quitando constantes.

¿Qué pasa si no existe la derivada de la función ni tampoco es posible obtenerla?

Entonces no se puede integrar por este método de integración y habría que saber cuál dependiendo de la forma de la integral. Lo tienes todo explicado al detalle en el Curso de Integrales Indefinidas.

Ejercicios propuestos

Resuelve las siguientes integrales por el método de integración de integrales inmediatas:

¿Necesitas clases de matemáticas? ¿Quieres que te explique cualquier duda que te surja?

Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.

He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.

Con mi método:

• Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
• Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión

Suena bien ¿no?

¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?

Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más:

ENSÉÑAME MATEMÁTICAS