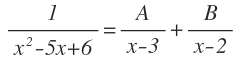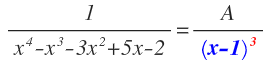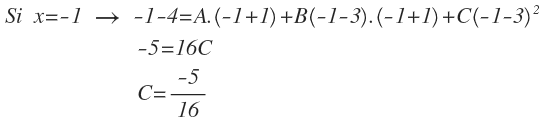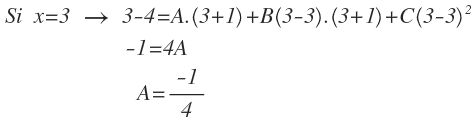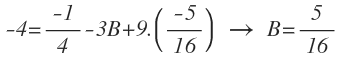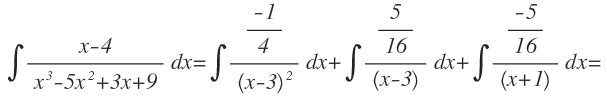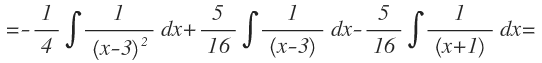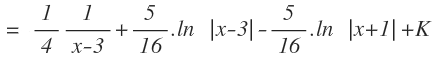A continuación te voy a explicar cuál es el procedimiento para resolver integrales racionales cuando el polinomio del denominador tiene raíces reales múltiples, al mismo tiempo que vamos resolviendo un ejemplo.
Si quieres saber cómo resolver integrales racionales cuando el denominador tenía raíces reales distintas, lo tienes explicado en el Curso de Integrales, donde te enseño a integrar paso a paso desde el principio.
Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Cómo resolver integrales racionales con raíces múltiples en el denominador
Antes de empezar a explicar como resolver este tipo de integrales vamos a dejar claro qué quiere decir que el denominador tenga raíces reales múltiples: que el denominador tenga raíces reales múltiples significa que al menos una de sus raíces se repite.
Vamos a verlo todo con un ejemplo:
Primero de todo debemos identificar qué método de integración hay que utilizar y para ello, debemos saber qué tipo de integral se trata.
Vamos a ir descartando métodos de integración.
No puede resolverse con ninguna integral inmediata de una función simple, ya que en el denominador tenemos una función con más de un término.
La integral inmediata de una función compuesta que más puede parecerse es la de tipo logarítmico:
Pero si intentamos resolverla con esta integral inmediata, necesitamos la función derivada del denominador, que tampoco podemos obtenerla, luego tampoco puede resolverse por ese método.
Una vez descartados los otros métodos de integración es cuando aplicamos el método de una integral racional. Tenemos por tanto la siguiente integral:
Que se trata de una integral racional donde el grado del polinomio del denominador es mayor que el grado del polinomio del numerador:
Ahora debemos factorizar el denominador. Como es un polinomio de grado tres, utilizamos la regla de Ruffini y nos queda:
Al factorizar podemos ver que x=3 es una raíz repetida del polinomio del denominador, por lo que tenemos raíces reales múltiples y por tanto hay que utilizar este método que te voy a explicar.
El procedimiento para resolver este tipo de integrales es similar al de las integrales racionales con raíces reales distintas en el denominador, ya que debemos descomponer la función racional en fracciones simples. La diferencia está en el denominador las fracciones simples.
Antes de seguir resolviendo nuestra integral, vamos a dejar claro cómo descomponer en fracciones simples cuando tenemos raíces reales múltiples en el denominador:
Con las raíces reales distintas, los denominadores de las fracciones simples eran cada uno de los factores del denominador de la función racional, una vez descompuesto, por ejemplo:
Pero cuando las raíces son múltiples, en los denominadores de las fracciones simples, debemos poner su factor correspondiente en forma de potencia y luego vamos sumando fracciones simples, cuyo denominadores serán el mismo factor de la raíz múltiple en forma de potencia, pero disminuyendo en uno el exponente, hasta que el exponente sea 1.
Por ejemplo, vamos a descomponer esta fracción en fracciones simples:
En primer lugar descomponemos el denominador, utilizando la regla de Ruffini al ser un polinomio de grado cuatro:
Nos queda:
Que expresando el factor que se repite en forma de potencia nos queda:
Como te he comentado antes ponemos el factor en forma de potencia como uno de los denominadores de las fracciones simples, es decir, ponemos (x-1)³ como denominador:
Ahora vamos sumando fracciones simples, cuyo denominadores serán el mismo factor de la raíz múltiple en forma de potencia, pero disminuyendo en uno el exponente, hasta que el exponente sea 1:
Y por último añadimos la siguiente fracción simple cuyo resultado corresponde con el factor de la raíz que no se repite:
A este método de obtener fracciones simples se le conoce como el método Alemán.
Bien, una vez hemos dejado claro esto, vamos a aplicar lo aprendido para seguir resolviendo nuestra integral. Nos quedamos en que habíamos factorizado el denominador, llegando a la conclusión de que tenía raíces reales múltiples:
Descomponemos la función racional en fracciones simples aplicando el método alemán: la primera fracción simple tendrá como denominador el factor correspondiente a la raíz repetida en forma de potencia, es decir (x-3)², la siguiente fracción simple será este mismo factor pero con su exponente disminuido en 1, es decir (x-3) y por último añadimos la última fracción simple que tendrá como denominador el factor que corresponde a la otra raíz:
Los numeradores de cada fracción simple son constantes que no conocemos y los hemos llamado A, B y C.
Vamos a obtener el valor de estas constantes.
En primer lugar realizamos la suma de las fracciones simples, reduciendo a común denominador (si no entiendes cómo dar este paso, lo tienes explicado paso a paso en el Curso de Fracciones Algebraicas):
Ahora igualamos el numerador de la fracción que acabamos de obtener con el numerador de la fracción original:
El siguiente paso es darle valores a la x. Le vamos a dar los valores de sus raíces, que harán que se anulen términos. Como tenemos tres constantes y sólo dos raíces, nos falta un valor para la x, que será el 0.
Podemos elegir cualquier número para darle valores a la x. Hemos elegido estos para simplificar cálculos.
Con x=-1:
Obtengo directamente el valor de C.
Con x=3:
Obtengo directamente el valor de A.
Con x=0:
Obtengo una ecuación que depende de A, B y C. Como ya sé el valor de A y C, sólo me queda sustituir y despejar para obtener el valor de B:
Una vez conocidos los valores de todas las constantes, escribimos nuestra integral como una suma de integrales de cada fracción simple obtenida:
Sacamos fuera las constantes:
Y las resolvemos mediante integrales inmediatas, llegando al resultado final de la integral:
Ejercicios propuestos
Resuelve las siguientes integrales:
¿Necesitas ayuda con las matemáticas? ¿Quieres que te explique cualquier duda que te surja paso a paso?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más:

Exámenes resueltos de Matemáticas II Selectividad (EBAU) Asturias

Exámenes resueltos de Matemáticas II Selectividad (EBAU) Extremadura

Exámenes resueltos de Matemáticas II Selectividad (PBAU) Baleares

Exámenes resueltos de Matemáticas II Selectividad (EBAU) Castilla y León

Exámenes resueltos de Matemáticas II Selectividad (EBAU) Canarias

Exámenes resueltos de Matemáticas II Selectividad (EAU) País Vasco

Exámenes resueltos de Matemáticas II Selectividad (EvAU) Navarra