La resolución de triángulos rectángulos consiste en calcular las medidas de sus tres lados y el valor de sus tres ángulos, cuando ya conocemos como mínimo dos de estos elementos.
Si has llegado hasta aquí es porque quieres aprender a resolver algún ejercicio. ¿Has pensado en apuntarte a clases de matemáticas online?. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
En este vídeo tienes ejercicios resueltos sobre resolución de triángulos rectángulos:
Y si sigues leyendo, lo tienes todo explicado con todo detalle.
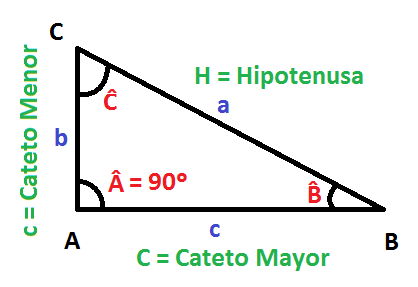
Triángulos rectángulos: ¿Qué elementos tienen? ¿Cómo se relacionan los elementos de un triángulo rectángulo?
Los triángulos en general, están formados por 3 lados y 3 ángulos. Además, los triángulos rectángulos se llaman así por tener un ángulo recto entre sus catetos.
Los lados de un triángulo rectángulo son la hipotenusa y los dos catetos:
El lado que está enfrente del ángulo recto es la hipotenusa:
A los otros dos lados, son los catetos: cateto mayor y cateto menor, que como su propio nombre indican, el cateto mayor es el que tiene una mayor longitud y el cateto menor es el que tiene una menor longitud.
Pero existe otra forma de denominar a los catetos, en función del ángulo que tomemos de referencia: el cateto opuesto y contiguo (o cateto adyacente).
¿Cómo identificar los catetos en un triángulo rectángulo?
Te voy a explicar cómo diferenciar entre el cateto opuesto y el cateto contiguo en función del ángulo de referencia.
¿Cómo saber cuál es el cateto opuesto?
Se le llama cateto opuesto al lado que esté enfrente del ángulo de referencia
¿Cómo saber cuál es el cateto contiguo o cateto adyacente?
Se le llama cateto contiguo al lado que esté tocando a ese ángulo.
Por ejemplo, en este triángulo:
Si tomamos de referencia el ángulo B:
b es el lado que está enfrente de B y c es el lado que está tocando al ángulo B.
Pero si tomamos como referencia al ángulo C:
Entonces b es el cateto contiguo y c es el cateto opuesto.
Por tanto, para saber cuál de todas las razones trigonométricas en el triángulo rectángulo, tienes que utilizar para resolver un problema, lo primero que tienes que hacer es identificar tus catetos con respecto al ángulo con el que estés calculándolas.
Los lados y ángulos del triángulo rectángulo, tienen una serie de relaciones entre ellos, las cuales nos van a ayudar a calcular las medidas de los elementos que no conozcamos.
- Los tres lados están relacionados por el teorema de Pitágoras:
- Los tres ángulos suman entre ellos 180º:
- Los lados y los ángulos se relacionan mediante las razones trigonométricas, las cuales te las explico con todo detalle en el siguiente apartado.
Razones trigonométricas de un triángulo rectángulo
Los ángulos y lados de un triángulo rectángulo, están relacionados por unas expresiones a las que llamamos razones trigonométricas.
Vamos ir viéndolas una por una, tomando como ángulo de referencia el ángulo B.
Seno del ángulo B
Relaciona el ángulo B con el cateto opuesto y la hipotenusa. En otras palabras, es la razón entre el cateto opuesto y la hipotenusa. Se expresa como sen B:
Coseno del ángulo B
Relaciona el ángulo B con el cateto contiguo y la hipotenusa. Es la razón entre el cateto contiguo y la hipotenusa. Se expresa como cos B:
Tangente del ángulo B
Es la razón entre el cateto opuesto y el cateto contiguo. También entre el seno y el coseno. Se expresa como tg B:
Cosecante del ángulo B
Es la razón inversa del seno. Se expresa como cosec B:
No hay que confundirlo con la función inversa del seno, que es el arco seno.
Secante del ángulo B
Es la razón inversa del coseno. Se expresa como sec B:
No hay que confundirlo con la función inversa del coseno que es el arco coseno.
Cotangente del ángulo B
Es la razón inversa de la tangente y se expresa como cotg B:
No hay que confundirlo por la función inversa de la tangente que es el arco tangente.
Como ves, todas la razones trigonométricas relacionan un ángulo con dos lados, es decir, tres variables. Por tanto, a la hora de elegir que razón utilizar, deberá ser aquella que sepamos al menos dos de las tres variables.
Tenemos que ir jugando con estas fórmulas según los datos que nos de el enunciado del problema.
Existen dos casos posibles que podemos encontrarnos en los problemas o ejercicios de resolución de triángulos rectángulos que son:
- Que conozcamos dos lados y nos pregunte por algún ángulo o el otro lado
- Que conozcamos un lado y un ángulo y nos pidan calcular cualquier otro lado o ángulo
Si nos dan como dato dos ángulos, no podremos calcular los lados de ese triángulo rectángulo. Necesitaríamos más información.
Siempre necesitamos como mínimo dos datos para calcular un tercero.
Resolución de triángulos rectángulos cuando se conocen dos lados
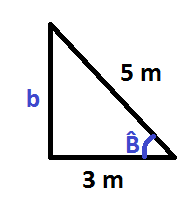
Vamos a ver, todo lo que te acabo de explicar con un ejemplo. Tenemos un triángulo del que conocemos 2 de sus lados:
Nos piden calcular el lado b y el ángulo B:
Para calcular el lado b, lo hacemos mediante la fórmula de Pitágoras, ya que en esa fórmula se relacionan los 3 lados y sólo nos queda por conocer 1 un lado.
De la fórmula de Pitágoras despejamos el cateto mayor, que corresponde con el lado b:
Y ahora sustituimos valores y calculamos:
- C = b (es el lado que estamos calculando)
- c = 3 m
- H = 5 m
Nos ha quedado una ecuación, de la que tenemos b como incógnita.
Para calcular el ángulo B, podemos hacerlo de muchas maneras. Una de ellas es utilizando la razón trigonométrica del seno por ejemplo, ya que conocemos el valor de la hipotenusa y del cateto opuesto.
En realidad podríamos utilizar cualquier razón trigonométrica porque conocemos todos sus lados:
Sustituimos valores y resolvemos:
Una vez conocemos el valor del seno de B, con la calculadora hemos calculado su inversa y obtenemos el ángulo. Presta atención a que la calculadora esté en grados y no en radianes.
Resolución de triángulos rectángulos cuando se conocen un lado y un ángulo
Vamos a ver otro ejemplo con este triángulo, del que conocemos un ángulo y un lado.
Nos piden calcular el lado c:
A priori, no se puede utilizar la fórmula de Pitágoras porque sólo tengo el dato de un lado. Por tanto, queda utilizar las razones trigonométricas.
Conocemos la hipotenusa y nos están pidiendo el lado adyacente. La razón que relaciona éstos dos lados es la del coseno:
Sustituimos los valores que conocemos y resolvemos:
- Ángulo B = 60º
- Cateto Adyacente = c
- Hipotenusa = 6 m
En este caso, el c0seno de 60, una vez resuelto con la calculadora, lo tratamos como un número más.
Ahora que ya conocemos c, podríamos utilizar Pitágoras para calcular el lado que nos queda, si nos lo estuvieran pidiendo.
Conforme vamos conociendo más elementos, tenemos la posibilidad de aplicar más relaciones para encontrar la solución que nos pidan.
La resolución de triángulos rectángulos tienen muchas aplicaciones, como calcular la distancia de un cable, calcular la altura de una torre, calcular la distancia de un árbol según su sombra, calcular el ángulo que forma una escalera apoyada en una pared o cualquier otra cosa que nos pueda pedir el enunciado de un problema.
Ejercicio resuelto de resolución de triángulos rectángulos
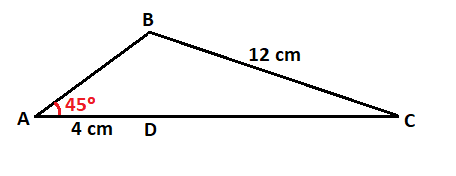
En el siguiente ejercicio, aplicaremos lo aprendido para calcular diferentes ángulos y lados de un triángulo, que en principio no es rectángulo.
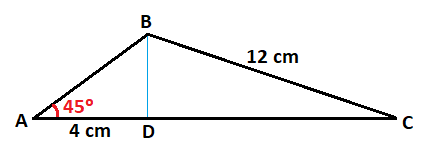
Calcular los lados y los ángulos del siguiente triángulo, del que nos dan uno de los ángulos, uno de los lados y la distancia desde el punto A hasta el punto D:
Lo primero que tienes que hacer es buscar triángulos rectángulos en este triángulo para poder resolverlo y calcular los elementos que faltan.
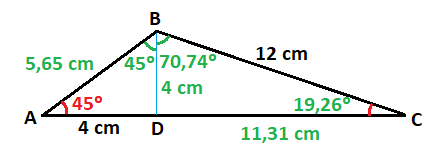
Para ello, trazamos una línea vertical que una al vértice B con el punto D, que es la altura del triángulo y lo divide en dos triángulos rectángulos:
Empezamos quedándonos con el triángulo de la izquierda:
En este triángulo falta por calcular el lado c y el lado h (les he llamado c y h por llamarles de alguna forma para distinguirlos).
Vamos a calcular el lado c. Conocemos el ángulo y el lado contiguo al ángulo, pero no conocemos el lado opuesto.
La razón que relaciona esas tres variables es la tangente:
De donde despejamos c:
La tangente de 45º la calculamos con la calculadora y finalmente operamos:
El lado c mide 4 cm.
Ahora calcularemos el lado h, mediante la razón del seno, ya que conocemos el ángulo, el cateto opuesto y no conocemos la hipotenusa:
Despejamos h:
Calculamos el seno de 45º con la calculadora y operamos:
El lado h mide 5,65 cm.
Otra forma de calcular h hubiera sido por el teorema de Pitágoras.
Finalmente vamos a calcular el ángulo que nos falta. Como sabemos que los lados de un triángulo deben sumar 180º, a 180º le restamos los dos ángulos que ya sabemos:
Por lo que el ángulo que falta mide 45º.
Colocamos todos los datos calculados en el triángulo rectángulo:
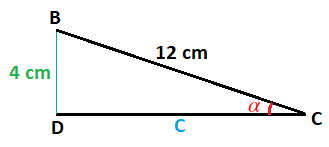
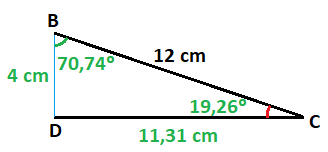
Hacemos lo mismo con el triángulo rectángulo que nos quedó a la derecha, donde colocamos el valor de uno de los lados que hemos calculado gracias al otro triángulo rectángulo:
De este triángulo faltaría por calcular el lado C y los dos ángulos que no son rectos.
Empezamos calculando el ángulo alfa. Lo haré mediante la razón del seno, que relaciona el cateto opuesto con la hipotenusa y tengo los dos datos:
Calculo el seno de alfa:
Y mediante la inversa del seno, calculo el ángulo:
El ángulo alfa mide 19,26º.
El lado C lo voy a calcular por Pitágoras esta vez:
El lado C mide 11,31 cm.
El ángulo que nos falta lo calcularemos sabiendo que los tres ángulos de un triángulo suman 180º y a 180º le restaré los dos ángulos que ya sabemos:
Coloco todos los datos en el triángulo
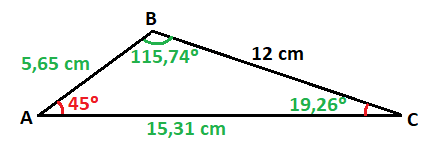
Ahora ya tengo todos los datos que necesito para calcular los lados y los ángulos del triángulo original
Para calcular el ángulo B, sumo los dos ángulos que he obtenido anteriormente:
Y para calcular el lado inferior, sumo el dato que ya tenía desde el punto A al punto D y el que he calculado desde el punto D al punto C:
Por lo que los lados y ángulos del triángulo original son:
¿Necesitas clases de matemáticas online? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más:




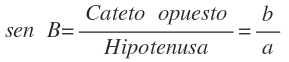
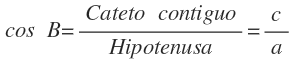



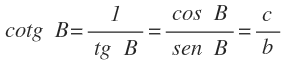





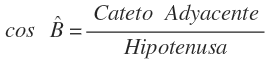
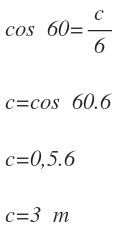

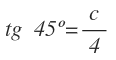
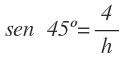




fue muy util la tarea