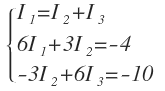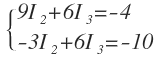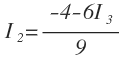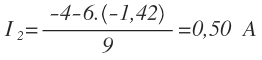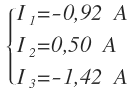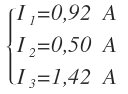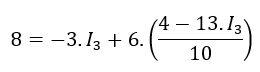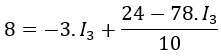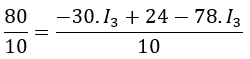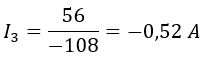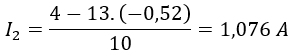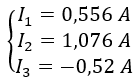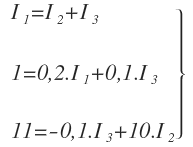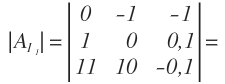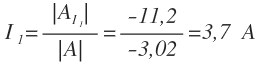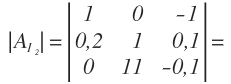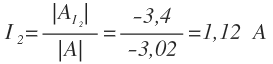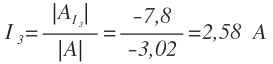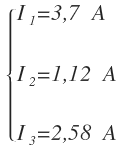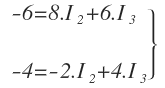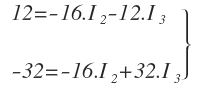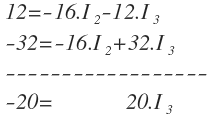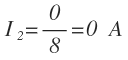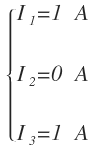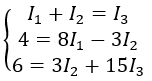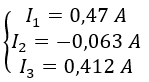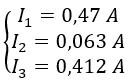Leyes de Kirchhoff. Ejercicios resueltos paso a paso

A continuación te voy a explicar las leyes de Kirchhoff, las cuales nos sirven para resolver circuitos y conocer el comportamiento de todos sus elementos activos y pasivos. Se trata de dos leyes: la primera ley de Kirchhoff o ley de las corrientes y la segunda ley de Kirchhoff o ley de las tensiones.

Veremos cada una de ellas detenidamente y resolveremos ejercicios aplicándolas.

Si has llegado hasta aquí es porque hay algún ejercicio que no sabes resolver y necesitas clases de electrotecnia online y es muy probable que también necesites refuerzo en matemáticas. Si después de leer esto, quieres seguir aprendiendo paso a paso, en una plataforma donde tengas todo explicado, con ejercicios resueltos y alguien que te resuelva tus dudas, solo tienes que apuntarte a los Cursos de Electrotecnia Online:

VER CURSOS DE ELECTROTECNIA ONLINE

Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas y electrotecnia. Puedo explicarte paso a paso cualquier duda que no entiendas.

Sólo tienes que dejarte guiar y verás como vas a aprendiendo poco a poco a resolver tus ejercicios de electrotecnia.

En este vídeo tienes explicado paso a paso un ejercicio resuelto sobre la aplicación de las leyes de Kirchhoff:

Y a continuación tienes toda la explicación que necesitas para entenderlo:

Conceptos previos de las leyes de Kirchhoff

Antes de empezar con las leyes de Kirchhoff es necesario que conozcas una serie de conceptos previos para entender mejor los enunciados.

• Elementos activos: Son los elementos de un circuito capaces de suministrar energía al circuito. Las fuentes de tensión son elementos activos.
• Elementos pasivos: Son los elementos de un circuito que consumen energía. Son elementos pasivos las resistencias, las inductancias y los condensadores.
• Nudo: Punto de un circuito donde concurren más de dos conductores
• Rama: Conjunto de todos los elementos comprendido entre dos nudos consecutivos
• Malla: Conjunto de ramas que forman un camino cerrado en un circuito, que no puede subdividirse en otros ni pasar dos veces por la misma rama

Por ejemplo, en el siguiente circuito:

Los elementos activos son los generadores:

Los elementos pasivos son las resistencias:

a, b, c y d son los nudos del circuito.

Tenemos seis ramas: ab, bd,  bc, ad, dc y ac y tres mallas: abda, dbcd y adca.

Primera ley de Kirchhoff. Ley de las corrientes de Kirchhoff

Las corrientes que entran y salen de un nudo están relacionadas entre sí por la ley de las corrientes de Kirchhoff, cuyo enunciado es el siguiente:

«La suma algebraica de todas las intensidades que llegan a un nudo es igual a la suma algebraica de todas las intensidades que salen del nudo, consideradas todas ellas en el mismo instante de tiempo»:

Por ejemplo, en el siguiente nudo «a», llegan las intensidades I1, I2 e I3 y salen las intensidades I4 e I5:

Por tanto, aplicando la primera ley de Kirchhoff nos quedaría:

La primera ley de Kirchhoff también se puede enunciar como que «la suma algebraica de todas las intensidades que concurren en un nudo es igual a cero»:

Se adopta el convenio de considerar positivas a las intensidades que llegan y negativas a las intensidades que salen.

En el nudo del ejemplo anterior:

Aplicando la ley de las corrientes de Kirchhoff con este segundo enunciado nos queda:

Segunda ley de Kirchhoff. Ley de las tensiones de Kirchhoff

El voltaje generado en un circuito se consume en las caídas de tensión que se producen en todas las resistencias conectadas en el mismo, ya que por la ley de Ohm, la tensión es igual al producto de la intensidad por la resistencia (V=I.R).

Las tensiones generadas y las caídas de tensión producidas en los receptores se relacionan entre sí por la ley de las tensiones de Kirchhoff, cuyo enunciado dice así:

«En toda malla o circuito cerrado, la suma algebraica de todas las tensiones generadas debe ser igual a la suma algebraica de las caídas de tensión en todas las resistencias a lo largo de la malla»:

Si el sumatorio del segundo miembro lo pasamos al primer miembro nos queda:

Expresión que nos permite enunciar la segunda ley de Kirchhoff de esta forma: «La suma algebraica de las tensiones a lo largo de una malla o circuito cerrado es igual a cero».

Convenio de signos en la segunda ley de Kirchhoff

Para aplicar esta ley, debemos tener en cuenta si la tensión del generador o la caída de tensión del receptor es positiva o negativa y esto lo establecemos con un convenio de signos.

Ojo, los convenios de signos que te voy a indicar a continuación son válidos en esta expresión:

ya que en la otra expresión que está igualada a cero, los signos de I.R cambiarían.

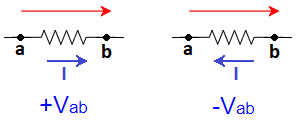
En los generadores, el convenio de signos para la tensión es el siguiente:

• Cuando recorremos un generador desde el borde negativo hasta el positivo, la tensión es positiva
• Cuando recorremos un generador desde el borde positivo hasta el negativo, la tensión es negativa

La flecha indica el sentido con el que se recorre la malla.

En las resistencias, el convenio de signos para la caída de tensión es:

• La caída de tensión será positiva si el sentido de la intensidad que circula por ella coincide con el sentido con el que se recorre la malla.
• La caída de tensión será negativa si el sentido de la intensidad que circula por ella es contrario al sentido con el que se recorre la malla.

Vamos a ver un ejemplo:

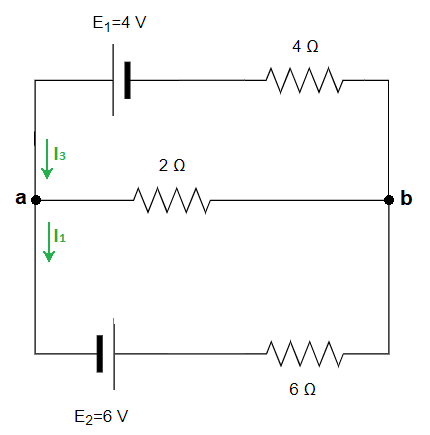
Vamos a aplicar la segunda ley de Kirchhoff al siguiente circuito en la malla con sentido a-b-d-a, donde tenemos también el sentido de las intensidades (veremos más abajo en el ejercicio cómo establecer el sentido de las intensidades):

Aplicamos la siguiente fórmula:

Para E1, el recorrido va del polo positivo negativo al positivo, luego la tensión es positiva. En las tres resistencias, la intensidad y el sentido con el que se recorre la malla es el mismo.

Ahora, pasamos todos los términos del segundo miembro restando al primer miembro y nos queda:

Es decir, nos queda que la suma de tensiones generadas, menos la suma de las caídas de tensión en los receptores es igual a cero:

Procedimiento para resolver circuitos con las leyes de Kirchhoff

Vamos a ver cuál es el procedimiento para resolver cualquier circuito aplicando las dos leyes de Kirchhoff. Es el siguiente:

1. Le asignamos una letra a cada nudo del circuito
2. Se dibujan las intensidades por cada rama, asignándoles un sentido al azar.
3. Se aplica la primera ley de Kirchhoff o la ley de las corrientes a tantos nudos tenga el circuito menos uno
4. Se aplica la segunda ley de Kirchhoff o la ley de las tensiones a todas las mallas del circuito
5. Tendremos tantas ecuaciones como número de intensidades tenga el circuito
6. Se resuelve el sistema de ecuaciones planteado, ya sea por el método de sustitución o aplicando la regla de Cramer si tenemos 3 ecuaciones o más
7. Las intensidades que tengan signo positivo, tienen el mismo sentido que le asignamos en el segundo paso. Las intensidades con signo negativo tienen sentido contrario al valor asignado inicialmente y debemos cambiarles el sentido.
8. Una vez tenemos el valor y sentido real de todas las intensidades, ya podemos hacer un balance de potencias y contestar a todas las preguntas sobre el análisis del circuito.

Ejercicios resueltos sobre las leyes de Kirchhoff

Vamos a resolver unos ejercicios, donde aplicaremos las leyes de Kirchhoff paso a paso, al mismo tiempo que te enseño a resolver ejercicios de este tipo.

Ejercicio 1

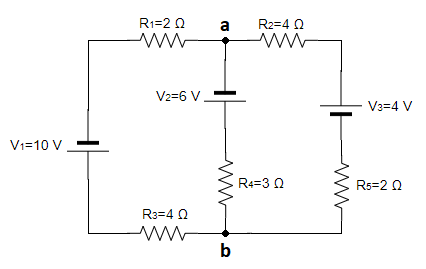
En el siguiente circuito, calcula las intensidades de cada una de sus ramas y realiza un balance de potencias:

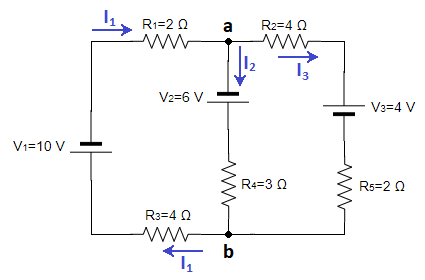
Ya tenemos las letras asignadas a los nudos. Seguimos dibujando las intensidades de cada rama asignando un sentido al azar:

Tenemos que aplicar la ley de las corrientes de Kirchhoff a tantos nudos tenga el circuito menos uno. Tenemos 2 nudos, el a y el b, luego se la tenemos que aplicar a uno de ellos. Se la aplico al nudo «a» y queda:

Ya tenemos la primer ecuación.

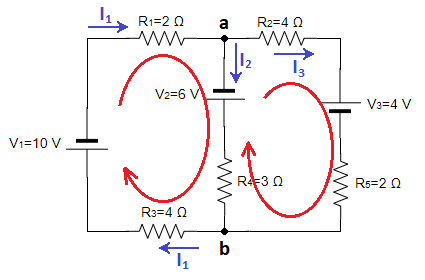
Seguimos aplicando la ley de las tensiones de Kirchhoff a todas las mallas del circuito. En nuestro caso tenemos dos mallas. En primer lugar, establecemos el sentido con el que recorreremos cada malla, que en mi caso será éste:

En la primera malla nos queda:

Operamos y reordenamos términos:

En la segunda malla nos queda:

Operamos y reordenamos términos:

Con la segunda ley de Kirchhoff, nos han salido dos ecuaciones más, teniendo tres en total, igual que el número de intensidades, que son éstas:

Vamos a resolver el sistema que nos ha quedado.

En la primera ecuación tengo I1 despejada en función de I2 e I3. Esa expresión de I1 la sustituyo en la segunda ecuación:

Elimino el paréntesis multiplicando I2 e I3 por 6:

Y agrupo términos:

Esta ecuación junto con la tercera ecuación del sistema inicial forman un sistema de dos ecuaciones con dos incógnitas, que paso a resolver por el método de sustitución:

En la primera ecuación:

Despejamos I2. Para ello primer pasamos el 6I3 restando al otro miembro:

Y después pasamos el 9 dividiendo al segundo miembro:

En la segunda ecuación:

Sustituimos I2 por la expresión obtenida anteriormente:

Eliminamos el paréntesis multiplicando el -3 por los términos del numerador:

Obtenemos denominador común:

Eliminamos denominadores:

Agrupamos términos y reordenamos:

Finalmente despejamos I3 y operamos:

En la expresión donde despejamos I2:

Sustituimos I3 por el valor que acabamos de calcular y operamos:

Ya tenemos el valor de I2 e I3, falta el valor de I1. En la primer ecuación del sistema de tres ecuaciones inicial:

Sustituimos los valores de I2 e I3 y operamos:

Nos han quedado los siguientes valores de las intensidades:

Tanto I1 como I3 son negativas, luego debemos cambiar el sentido asignado inicialmente. I2 es positiva, luego el sentido que le asignamos al principio es el real. Las intensidades en el circuito quedan de la siguiente forma:

Una vez las intensidades tienen el sentido correcto, sus valores son todos positivos:

Ahora que tenemos el valor de todas las intensidades del circuito vamos a realizar el balance de potencias, que no es más que calcular la potencia generada por los generadores de tensión y la potencia consumida por la resistencia y luego analizar si la potencia generada es suficiente para abastecer a todos los receptores.

La potencia generada por el circuito es igual a la suma de las potencias de cada generador, que será igual a la tensión de cada generador por la intensidad que la recorre:

En nuestro caso I1 circula por V1, I2 circula por V2 e I3 circula por V3:

Sustituimos los valores de las intensidades y tensiones y operamos:

Seguimos calculando la potencia consumida por el circuito, que es igual a la suma de la potencia de cada resistencia, calculada como el valor de cada resistencia multiplicada por la intensidad que la recorre al cuadrado:

I1 circula por R1 y R3, I2 circula por R4 e I3 circula por R2 y R5:

Sustituimos los valores de las intensidades y resistencias y operamos:

Para que el circuito funcione con normalidad, la potencia generada debe ser mayor que la consumida.

En nuestro caso, la potencia generada y la consumida son prácticamente iguales (la diferencia tal vez se deba al redondeo decimales), por lo que el circuito estaría compensado.

En el caso de que la potencia consumida sea mayor que la generada, el circuito no podría funcionar y estaríamos ante un caso de sobrecarga.

Ejercicio 2

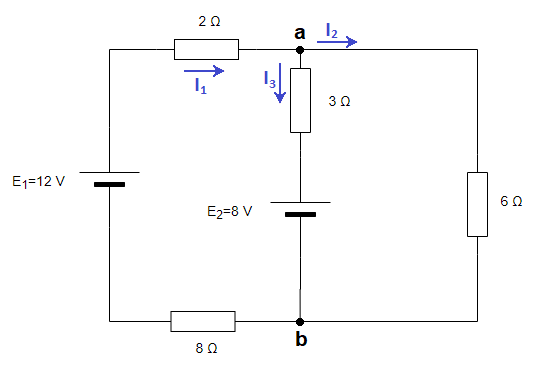
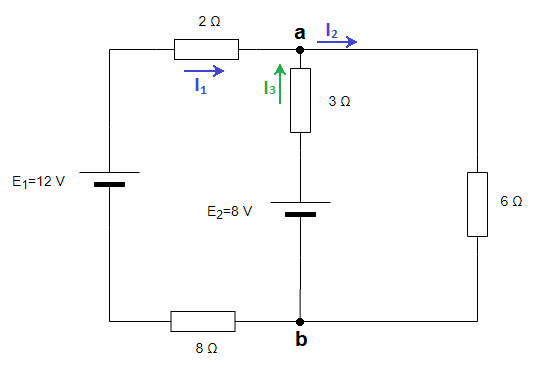
En el siguiente circuito, calcula la intensidad en cada rama y la potencia disipada en las resistencias de 3 y 8 ohmios:

En primer lugar, asignamos letras a los nudos y dibujamos las intensidades en cada rama, con un sentido arbitrario:

Aplicamos la primera ley de Kirchhoff a uno de los nudos, por ejemplo al nudo «a»:

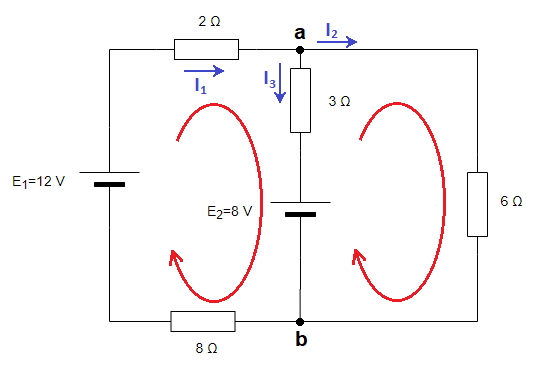
Seguimos aplicando la segunda ley de Kirchhoff a las dos mallas del circuito. Para ello, establecemos el sentido con el que recorreremos cada malla:

Para la malla de la izquierda nos queda:

Operamos agrupando términos semejantes:

En la malla de la derecha nos queda:

Aplicando las leyes de Kirchhoff, hemos obtenido tres ecuaciones, con las tres incógnitas (intensidades I1, I2 e I3):

Vamos a resolver el sistema. Lo haremos por el método de sustitución.

En la primera ecuación ya tenemos despejada I1:

En la segunda ecuación:

Sustituyo I1 por su expresión equivalente en función de I2 e I3:

Eliminamos el paréntesis multiplicando el 10 por cada uno de los términos del interior del paréntesis:

Agrupamos términos semejantes:

Esta ecuación, junto con la tercera ecuación del sistema de ecuaciones original, forman un sistema de dos ecuaciones con dos incógnitas (I2 e I3), que resolveremos por el método de sustitución:

En la primera ecuación:

Despejamos I2:

En la segunda ecuación:

Sustituyo I2 por la expresión que acabamos de obtener:

Eliminamos el paréntesis multiplicando el 6 por cada uno de los términos del numerador:

Obtenemos denominador común:

Y eliminamos paréntesis:

Por último, reagrupamos términos semejantes:

Y despejamos I3:

En la expresión donde despejamos I2:

Sustituimos I3 por su valor y operamos:

Con el valor de I2 e I3 ya podemos calcular el valor de I1.

En la primera ecuación del sistema original:

Sustituimos I2 e I3 por sus valores y operamos:

Los valores de las intensidades que hemos obtenido son:

Por tanto, hay que cambiar el sentido asignado a I3:

Los valores de las intensidades con su sentido correcto son:

Una vez tenemos las intensidades de cada rama vamos a calcular la potencia en las resistencias de 3 y 8 ohmios.

Para calcular la potencia utilizaremos la siguiente fórmula:

Donde la intensidad será la que circule por la resistencia en cuestión en cada caso

Para calcular la potencia en la resistencia de 3 ohmios, tenemos en cuenta que la intensidad que circula por ella es I3:

Sustituimos I3 por su valor y operamos:

La intensidad que circula por la resistencia de 8 ohmios es I1, por lo que la fórmula para calcular su potencia queda:

Sustituimos I1 por su valor y operamos:

Ejercicio 3

En el siguiente circuito, calcular la tensión que aparece en los bornes de la lámpara, así como la intensidad y potencia de la misma:

Asignamos letras a los nudos y dibujamos las intensidades en cada rama con sentido al azar:

Aplicamos la primera ley de Kirchhoff a uno de los nudos, por ejemplo al nudo «a»:

Aplicamos la segunda ley de Kirchhoff a las dos mallas del circuito, por lo que establecemos el sentido para recorrer cada malla:

En la malla de la izquierda nos queda:

Reagrupamos términos:

En la malla de la derecha tenemos:

Nos queda un por tanto un sistema de tres ecuaciones, cuyas tres incógnitas son I1, I2 e I3:

En este caso, vamos a resolver el sistema de ecuaciones con la regla de Cramer.

Para ello, colocamos las incógnitas en orden en el primer miembro, es decir, primero el término con I1, después el término con I2 y por último el término con I3 y en el segundo miembro dejamos los términos que no tengan incógnita o términos independientes:

Obtenemos el determinante de la matriz de los coeficientes.  Los coeficientes son los números que multiplican a las incógnitas. Si en alguna ecuación nos falta algún término, ponemos un 0:

Aplicamos la regla de Sarrus para resolver el determinante:

Y operamos:

El valor del determinante es distinto de cero:

por lo que estamos ante un sistema compatible determinado, por lo que este sistema tiene solución y podemos resolverlo aplicando la regla de Cramer.

Empezamos obteniendo el determinante asociado a I1, sustituyendo la primera columna por los términos independientes:

Aplicamos la regla de Sarrus:

Y operamos:

I1 es igual al valor del determinante asociado a I1 entre el valor del determinante de la matriz de los coeficientes:

Obtenemos el determinante asociado a I2, sustituyendo la segunda columna por los términos independientes:

Aplicamos la regla de Sarrus:

Y operamos:

I2 es igual al valor del determinante asociado a I2 entre el valor del determinante de la matriz de los coeficientes:

Por último, obtenemos el determinante asociado a I3, sustituyendo la tercera columna por los términos independientes:

Aplicamos la regla de Sarrus:

Y operamos:

I3 es igual al valor del determinante asociado a I3 entre el valor del determinante de la matriz de los coeficientes:

Los valores de las intensidades que hemos obtenido son:

Todas son positivas, lo que quiere decir que el sentido asignado al principio es el correcto:

Vamos a calcular la tensión en la lámpara que es igual a la intensidad I2 por el valor de la resistencia:

Sustituimos valores y operamos:

La potencia en la lámpara la calculamos con la siguiente fórmula:

Sustituimos I2 y R por sus valores y operamos:

Ejercicio 4

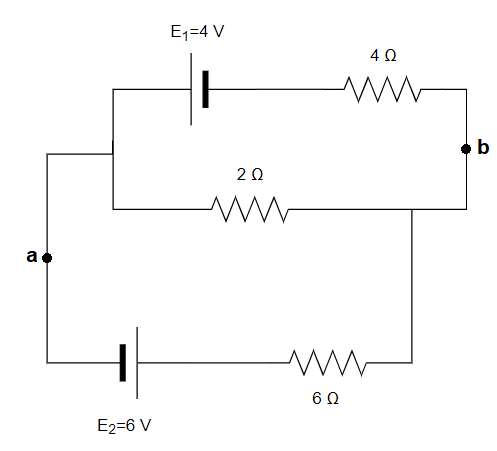
En el siguiente circuito, calcular la corriente en la resistencia de 2 ohmios, así como la tensión entre sus bornes y la potencia disipada:

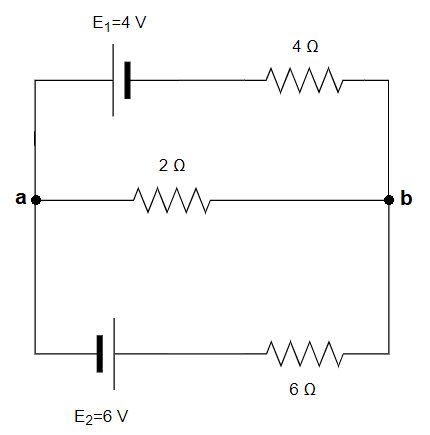
Este circuito es equivalente a este otro, donde se ve más clara la aplicación de las leyes de Kirchhoff:

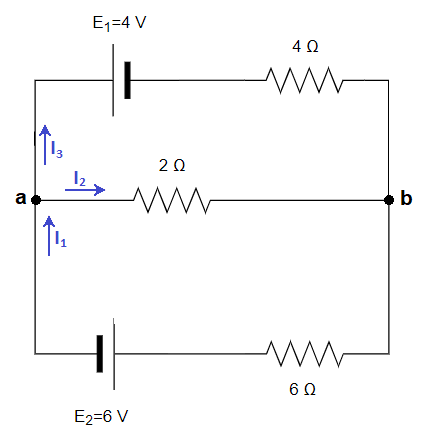
Dibujamos las intensidades de cada rama, asignándoles un sentido al azar:

Aplicamos la primera ley de Kirchhoff a uno de los nudos, por ejemplo al nudo «a»:

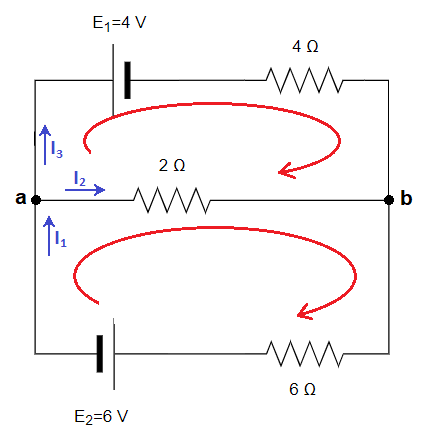
Aplicamos la segunda ley de Kirchhoff a las dos mallas del circuito. El sentido para recorrer cada malla es:

En la malla superior nos queda:

En la malla inferior nos queda:

Tenemos un sistema de tres ecuaciones con las tres intensidades como incógnitas:

En esta ocasión, vamos a aplicar el método de reducción para resolver el sistema.

Pero antes, en la primera ecuación, tenemos despejada I1:

En la segunda ecuación:

Sustituimos I1 por su expresión equivalente en función de I2 e I3:

Operamos para eliminar el paréntesis:

Y reagrupamos términos:

Esta ecuación junto con la tercera ecuación del sistema original forma un sistema de dos ecuaciones con dos incógnitas, que es el que resolveremos por el método de reducción:

Para anular I2, multiplico la primera ecuación por -2 y la segunda ecuación por 8:

Sumo ambas ecuaciones:

Del resultado de la suma, despejo I3:

En la primera ecuación:

Sustituyo I3 por su valor:

Opero y despejo I2:

En la ecuación donde tengo despejada I1:

Sustituyo I2 e I3 por sus valores y opero:

Los resultados obtenidos de cada intensidad son:

I1 e I3 son negativas, lo que quiere decir que tengo que cambiar el sentido asignado de ambas intensidades. I2, al ser nula, no la representamos. El circuito queda:

Los valores reales de las intensidades son:

La tensión entre los bornes de al resistencia de 2 ohmios es igual a la tensión entre los puntos a y b, que la calculamos multiplicando I2 por la resistencia:

Como I2 es igual a 0, tampoco tendremos tensión en esta resistencia:

La potencia en esta resistencia la calculamos con la siguiente fórmula:

Que como la intensidad I2 es igual a 0, no disipa ninguna potencia:

Ejercicio 5

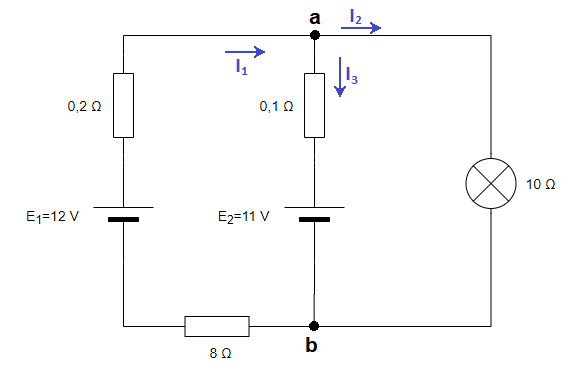
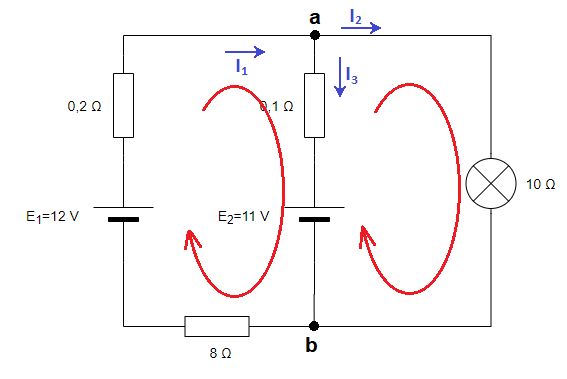
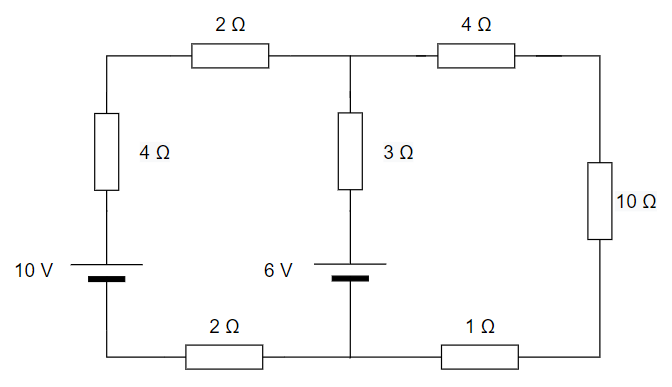
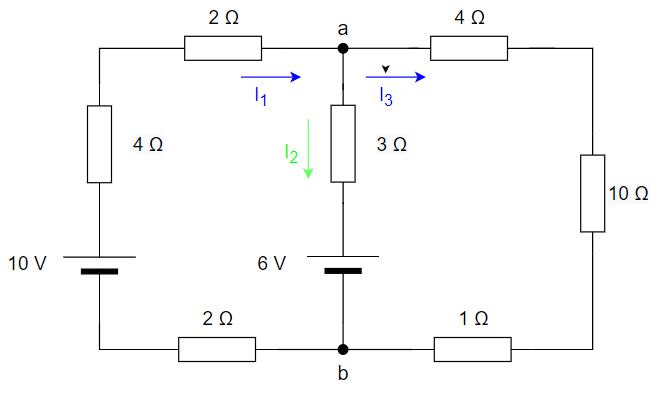
En el siguiente circuito, calcula la intensidad que circula por la resistencia de 10 ohmios y la tensión entre sus bornes:

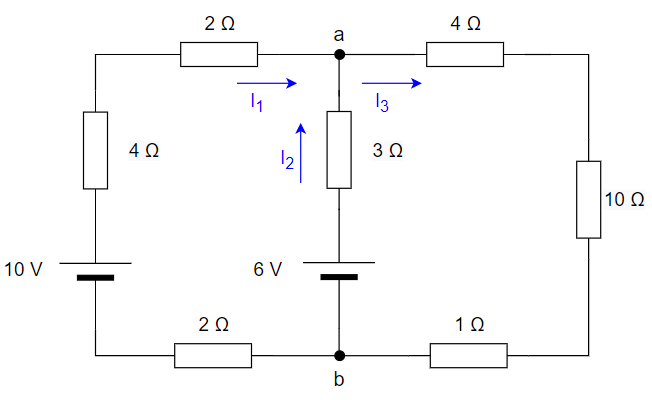
Empezamos nombrando los nudos y dibujando las intensidades por las ramas. Consideramos en un principio que las intensidades salen del polo positivo de los generadores de tensión:

Aplicamos la primera ley de Kirchhoff en el punto «a»:

Seguimos aplicando la segundo ley de Kirchhoff a cada malla. Establecemos el sentido que recorre las mallas:

En la malla izquierda:

Operamos y reagrupamos términos:

En la malla derecha:

Operamos y reagrupamos términos:

Nos queda el siguiente sistema de ecuaciones:

Cuyas soluciones son:

Como I2 nos ha quedado negativa, le cambiamos el sentido para volerla positiva:

Los valores de las intensidades con su sentido correcto son:

La intensidad que circula por la resistencia de 10 Ω es igual a I3:

Y calculamos la tensión de la resistencia de 10 Ω multiplicando el valor de la resistencia por I3 que es la intensidad que circula por ella:

¿Necesitas ayuda en electrotecnia y matemáticas? ¿Quieres que te explique cualquier duda que te surja?

Puedo enseñarte exactamente lo que necesitas aprender para entender electrotecnia y las matemáticas que necesitas aplicar.

He diseñado un método práctico y efectivo que te ayudará a entender la electrotecnia así como las matemáticas que necesitas aplicar, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.

Con mi método:

• Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas de electrotecnia
• Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión

Suena bien ¿no?

¿Por qué tardar 2 horas buscando información por Internet si puedes aprenderlo en menos de 20 minutos?

Te explicaré lo que necesitas aprender para entender electrotecnia y las matemáticas que necesitas aplicar. ¿Quieres informarte de como puedes aprender electrotecnia y matemáticas? Pulsa el botón para saber más:

ENSÉÑAME ELECTROTECNIA