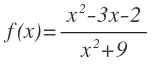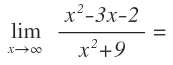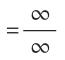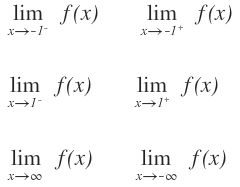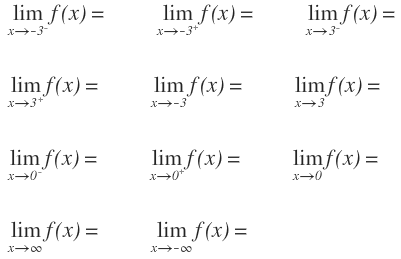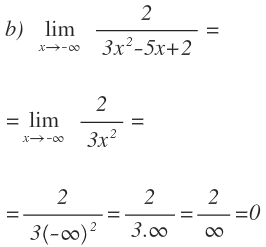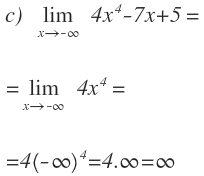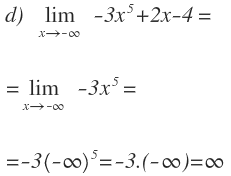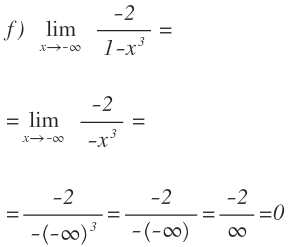A continuación te voy a explicar cómo resolver límites de funciones cuando x tiende a infinito o a menos infinito, con ejercicios resueltos paso por paso.
Veremos también que hay límites de funciones que aún tendiendo la x a un número finito, el resultado es infinito.
¡Vamos allá!
Si has llegado hasta aquí es porque quieres aprender a resolver algún ejercicio. ¿Has pensado en apuntarte a clases de matemáticas online?. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Si quieres seguir aprendiendo cómo resolver límites, en el Curso de Límites, te explico con todo detalle como resolver los límites de todos los tipos de indeterminaciones, con ejercicios resueltos paso a paso.
En este vídeo tienes ejercicios resueltos paso a paso sobre límites al infinito, es decir, límites cuando x tiende a más infinito o a menos infinito:
Y a partir de aquí, lo tienes todo explicado con todo detalle:
Límite de una función cuando x tiende a infinito
Para calcular el límite de una función cuando los valores de x crecen cada vez más, se indica que calculamos el límite de una función cuando x tiende a infinito.
Límite de una función cuando x tiende a infinito cuyo resultado es infinito
Hay funciones, que cuando x es cada vez mayor, el valor de su función también crece. En ese caso, cuando x tiende a infinito, el límite de la función también es infinito:
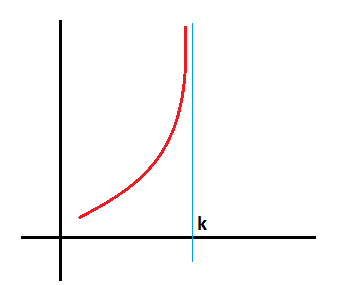
Gráficamente, funciones que se comportan así pueden tener esta forma:
Como vemos, cuando los valores de x son cada vez mayores, los valores de la función también son cada vez mayores y por tanto, la función tiende a irse hacia arriba y el límite de la función cuando x tiende a infinito es infinito.
¿Qué funciones tienen este comportamiento cuando x tiende a infinito?
Las funciones cuyo valor va creciendo conforme lo hacen los valores de x son las funciones polinómicas:
Las funciones exponenciales cuya base sea mayor que 1:
Y las funciones logarítmicas:
Límite de una función cuando x tiende a infinito cuyo resultado es menos infinito
En las funciones cuyo valor decrece conforme van aumentando los valores de x, el límite de la función cuando x tiende a infinito será menos infinito:
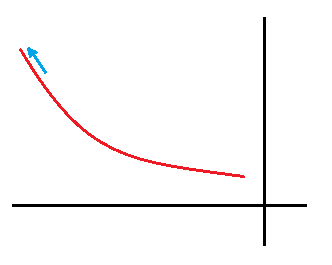
Si representamos una función de este tipo, tiene esta forma:
Donde como vemos, a medida que nos vamos moviendo hacia la derecha en el eje x, es decir, los valores de x van aumentando, los valores de la función son cada vez más pequeños. La función tiende a irse hacia abajo y el límite de la función cuando x tiende a infinito es menos infinito.
Las funciones cuyo valor se va haciendo más pequeño conforme aumentan los valores de x, son las mismas que en el caso anterior pero precedidas por un signo menos:
Límite de una función cuando x tiende a infinito cuyo resultado es un número
Existen funciones, que conforme van aumentando los valores de x, su valor se va aproximando cada vez más a un número:
Si representamos este caso, sería de la siguiente forma:
Conforme van aumentando los valores de x, el valor de la función está cada vez más cerca de valer k. El límite de la función cuando x tiende a infinito es igual a k.
En este caso, se dice que en y=k hay una asíntota horizontal.
Una asíntota es una línea a la que la función se aproxima cada vez más pero que nunca llega a tocar. Te lo explico más en detalle en el Curso de Límites. Ahora sólo quédate con que el límite de una función cuando x tiende a infinito puede dar como resultado un número.
¿Qué tipo de funciones dan como resultado un número en el límite cuando x tiende a infinito?
Las funciones racionales en las que el grado del numerador y el grado del denominador son iguales, como por ejemplo:
Límite de una función cuando x tiende a menos infinito
Para calcular el límite de una función cuando los valores de x cada vez se van haciendo más pequeños, se indica que calculamos el límite de una función cuando x tiende a menos infinito.
Límite de una función cuando x tiende a menos infinito cuyo resultado es infinito
Hay funciones, que cuando x es cada vez menor, el valor de su función es cada vez más grande. En ese caso, cuando x tiende a menos infinito, el límite de la función también es infinito:
Las funciones que se comportan así, tienen esta forma gráficamente:
Conforme nos vamos moviendo hacia la izquierda en el eje x, los valores de x van disminuyendo, los valores de la función son cada vez más grandes. La función tiende a irse hacia arriba y el límite de la función cuando x tiende a menos infinito es infinito.
Límite de una función cuando x tiende a menos infinito cuyo resultado es menos infinito
En las funciones cuyo valor decrece conforme van disminuyendo los valores de x, el límite de la función cuando x tiende a menos infinito será menos infinito:
Gráficamente, las funciones tienen la siguiente forma:
A medida que nos vamos moviendo hacia la izquierda en el eje x, los valores de la función son cada vez más pequeños. La función tiende a irse hacia abajo y el límite de la función cuando x tiende a menos infinito es menos infinito.
Límite de una función cuando x tiende a menos infinito cuyo resultado es un número
Existen funciones, que conforme van disminuyendo los valores de x, su valor se va aproximando cada vez más a un número en concreto:
La representación gráfica de este tipo de funciones sería así:
Conforme van decreciendo los valores de x, el valor de la función está cada vez más cerca de tomar el valor k. El límite de la función cuando x tiende a menos infinito es igual a k.
Al igual que pasaba cuando x tiende a infinito, aquí también se dice que en y=k hay una asíntota horizontal.
En este caso de los límites de funciones cuando x tiende a menos infinito no he comentado nada de las funciones que se comportan de estas maneras, porque son las mismas que para cuando x tiende a infinito, a excepción de la función logarítmica, ya que un logaritmo no existe para valores iguales o menores que cero.
Cómo resolver límites cuando x tiende a infinito
Una vez sabemos qué resultado puede tener el límite de una función cuando x tiende a infinito y qué forma pueden tener sus gráficas, voy a pasar a explicarte cómo calcular este tipo de límites.
A priori, no sabemos que resultado va a tener el límite de una función cuando x tiende a infinito. Lo sabemos cuando sustituimos la x por infinito.
Vamos a ir viendo cómo se resuelven los límites de cada tipo de función.
Límite de funciones polinómicas cuando x tiende a infinito
Por ejemplo:
En primer lugar, sustituimos la x por infinito:
Cuando resolvemos límites de este tipo, al sustituir por infinito, debemos tener en cuenta que el infinito de por sí ya tiene un valor muy grande. Si el infinito lo elevamos a algún exponente, todavía se hace más grande.
Entonces infinito elevado al cubo es muchísimo mayor que infinito elevado al cuadrado, incluso que el resto de operación que queda.
Para que lo entiendas mejor, imagina que estás calculando con un número muy muy grande y lo elevas al cubo. Si le restas el mismo número elevado al cuadrado, quedará todavía un número muy grande.
Pues este mismo concepto pero llevado hasta el extremo es lo que pasa cuando operamos con infinito, como es este caso. El valor de infinito al cubo es mucho mayor que el resto de la operación, de hecho, el resto de la operación ya da igual, porque es es despreciable y apenas le afecta.
Por tanto, el resultado del límite será infinito:
De hecho, el límite de una función polinómica cuando x tiende a infinito, es igual al límite de su término de mayor grado, por lo para calcular su solución es equivalente a calcular el límite del término de mayor grado:
Vamos a ver otro ejemplo:
Como te he comentado antes, calcular el límite de un polinomio cuando x tiende a infinito es equivalente a calcular el límite del término de mayor grado, por lo que lo hacemos así:
Sustituimos la x por infinito:
Por un lado, infinito a elevado a 4 sigue siendo infinito, un infinito mucho más grande que antes, pero como está solo, podemos seguir poniendo infinito.
Por otro lado, las operaciones con infinito responden a las reglas de signos. Por tanto, al multiplicar infinito por un número negativo, el resultado es menos infinito, que es el resultado del límite:
Vamos a ver ahora como resolver el límite de una función, donde el polinomio se encuentra en el denominador:
Siguiendo el mismo razonamiento que para los ejercicios anteriores, nos quedamos con el término de mayor grado en el denominador:
Ahora sustituimos la x por infinito. El resultado en el denominador es infinito y cualquier número entre infinito es igual a cero:
En general, los límites cuando x tiende a infinito de las funciones que tengan un número en el numerador y un polinomio en el denominador, su resultado será 0.
Seguimos con el límite de una función logarítmica:
Sustituimos la x por infinito. El valor de la función logarítmica es mayor cuanto mayor sea el valor de x, por lo que el logaritmo de infinito es infinito:
Si la función logarítmica tiene un signo menos delante, el resultado sería menos infinito:
Por último, vamos a ver qué pasa con las funciones racionales, donde el grado del numerador y el grado del denominador son iguales, cuando x tiende a infinito:
Al sustituir la x por infinito llegamos a una indeterminación:
La forma de resolver este límite te lo explico en el Curso de Límites cuando explico los tipos de indeterminaciones y cómo se resuelven.
Cómo resolver límites cuando x tiende a menos infinito
Te voy a explicar ahora cómo resolver límites de funciones cuando x tiende a menos infinito.
La forma de resolver los límites de funciones cuando x tiende a menos infinito es la misma para cuando x tiende a infinito, es decir, en funciones polinómicas, nos quedaremos con el término de mayor grado, ya que es el término que determinará el resultado de la operación.
Como te he comentado antes, las operaciones con infinito siguen la regla de los signos. Veíamos que si un número negativo multiplica a infinito, se convierte en menos infinito. Ten en cuenta que menos infinito no es más que infinito multiplicado por menos 1:
Cuando sustituimos la x por menos infinito, además de afectar la multiplicación de números negativos, también afecta en gran medida las potencias.
Menos infinito elevado a un número par será más infinito, igual que pasa con los números:
De la misma forma, si menos infinito está elevado a un número impar, su resultado será menos infinito:
Teniendo todo esto en cuenta, vamos a resolver unos cuantos límites de funciones cuando x tiende a menos infinito.
Empezamos con este:
Nos quedamos con el término de mayor grado:
Sustituimos por menos infinito. Como está elevado a un número par, el resultado es infinito:
Veamos otro ejemplo:
Nos quedamos con el término de mayor grado:
Sustituimos la x por menos infinito. Como está elevado a un número impar, el resultado es menos infinito:
Seguimos con otro ejemplo:
Nos quedamos con el término de mayor grado:
Sustituimos la x por menos infinito. En este caso tenemos un signo menos delante de la x. Por tanto, menos infinito elevado a 5, sigue siendo menos infinito, pero como tiene delante un signo menos, el resultado del límite es infinito:
Por último, vamos a ver cómo resolver un límite de una función cuando el polinomio está en el denominador:
Nos quedamos en el denominador con el término de mayor grado:
Y sustituimos la x por menos infinito. Al estar elevado a un número impar, el resultado es menos infinito en el denominador. No obstante, aunque 1 esté dividido entre menos infinito, el resultado sigue siendo cero, porque el cero no tiene signo:
Límites infinitos cuando x tiende a un número finito
Hasta ahora hemos estado viendo límites de funciones cuando x tiende a infinito o menos infinito, cuyo resultado puede ser infinito, menos infinito o un número.
También existen los límites cuando x tiende a un número cuyo resultado puede ser más o menos infinito:
Este tipo de límites se resuelven mediante límites laterales, tanto gráfica como analíticamente.
Vamos a analizar las diferentes situaciones que puedes tener cuando x tienda a un número y el resultado de límite sea infinito.
El límite de una función cuando x tiende a un número por la izquierda y el resultado es infinito:
Vemos que cuando en el eje xnos acercamos por la izquierda a un valor x=k (o x=n), la función tiende a irse hacia arriba y por tanto, cuanto más nos acercamos por la izquierda, su límite es infinito:
Puede darse el caso, de que nos aproximemos a un número por la derecha y el límite de esa función sea infinito:
En ese caso, la gráfica sería de esta manera, donde vemos que la función tiende a irse hacia arriba conforme nos acercamos por la derecha en el eje x a un número determinado:
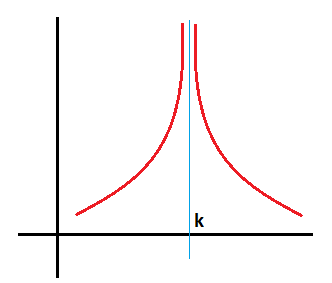
Cuando nos acercamos por la izquierda y por la derecha y en ambos casos el límite es infinito, entonces existe el límite de la función cuando x tiende a n, que es igual a infinito:
Cuya gráfica es de la siguiente forma:
También puede ser que cuando nos acerquemos a un ese número por la izquierda en el eje x, la función tienda a irse hacia abajo, por lo que el límite sería menos infinito:
Y la gráfica sería algo como esto:
O lo mismo cuando nos acerquemos por la derecha:
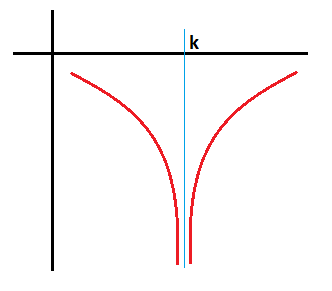
Si el límite por la derecha y el límite por la izquierda coinciden, entonces existe el límite de la función cuando x tiende a un número y su resultado es menos infinito:
La gráfica cuando existe el límite sería de la siguiente forma:
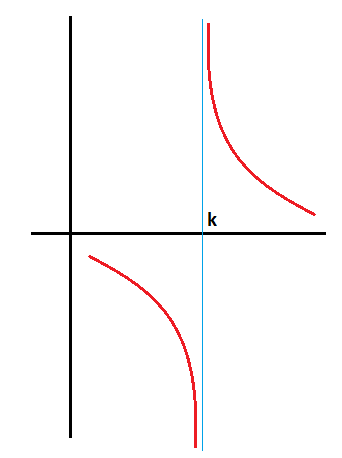
Puede darse el caso de que los límites laterales no coincidan, es decir, que por ejemplo el límite de la función cuando x tiende al número por la izquierda sea menos infinito y el límite por la derecha sea más infinito (o viceversa). En ese caso, existen los límites laterales, pero no existe el límite de la función cuando x tiende a ese número:
La función en este caso podría tener esta forma:
En todos los casos, tenemos una asíntota vertical en x=k (veremos el tema de las asíntotas con más detalle durante el curso, no te preocupes)
Vamos a ver un ejercicio sobre lo que acabamos de ver: Calcula los siguientes límites de la siguiente función:
Vamos a ir resolviendo cada uno de ellos.
Cuando x se aproxima a -1 por la izquierda, el límite es igual a menos infinito, ya que la función tiende a irse hacia abajo:
Cuando x se aproxima a -1 por la derecha, el límite es igual a infinito, ya que la función tiende a irse hacia arriba:
Cuando x se aproxima a 1 por la izquierda, el límite es igual a infinito, ya que la función tiende a irse hacia arriba:
Cuando x se aproxima a 1 por la derecha, el límite es igual a menos infinito, ya que la función tiende a irse hacia abajo:
Cuando x tiende a infinito la función se aproxima al valor -1, luego su límite es -1:
Lo mismo pasa cuando x tiende a menos infinito
En el Curso de Límites te enseño también a resolver analíticamente las funciones donde x tiende a infinito y el resultado es un número.
Ejercicios propuestos
1- Calcula los siguientes límites
2- Calcula los siguientes límites a partir de la siguiente función:
¿Necesitas ayuda con las matemáticas? ¿Quieres que te explique paso a paso cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: