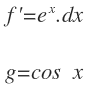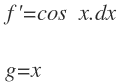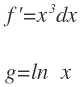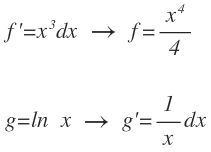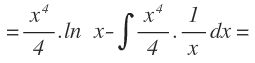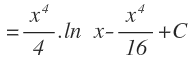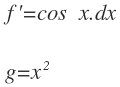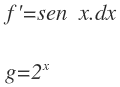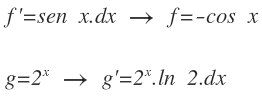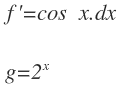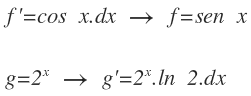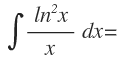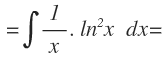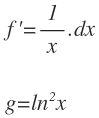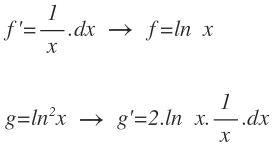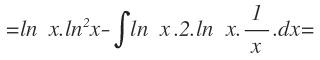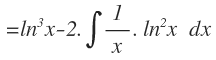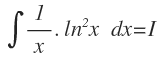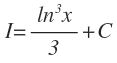Cuando no es posible transformar la integral para poder utilizar las integrales inmediatas, utilizamos el método de integración por partes, que es lo que veremos en esta lección.
Por cierto, el método de integración por integrales inmediatas y el resto de métodos de integración los tienes explicados con detalle en el Curso de Integrales Indefinidas. Además, al acceder a este curso, tienes acceso a todos los curso de la plataforma y puedes preguntarme cualquier duda que te surja.
Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
¡Vamos allá!
Integración por partes
El método de integración por partes se basa en la siguiente fórmula:
Se utiliza cuando no es posible integrar por medio de las integrales inmediatas, ya que no es posible transformar la integral para que se parezca alguna de sus fórmulas.
Date cuenta, que en la solución de la fórmula de integración por partes queda otra integral. Esa integral, podrá resolverse otra vez por partes o por medio de integrales inmediatas. El proceso es iterativo, es decir, hay que repetirlo una y otra vez.
Si se resuelve otra vez por partes, hay que ver si la integral es más sencilla que la original y por tanto vamos por buen camino y hay que seguir iterando el método hasta llegar a una integral que se resuelva por medio de integrales inmediatas y por tanto que lleguemos a una solución sin integrales.
Para integrar por partes debemos identificar dentro de la integral una función f’, que habrá que integrar y una función g que habrá que derivar:
Una vez hemos integrado f y derivado g, tenemos las 4 funciones que necesitamos para aplicar la fórmula de integración por partes y sólo tenemos que sustituirlas.
Todo esto lo verás más fácil cuando empecemos a resolver ejemplos de integración por partes.
Cómo elegir la función a integrar y la función a derivar en el método de integración por partes
Antes de empezar a resolver integrales por partes, te voy a dejar unas indicaciones para que tengas algún criterio a la hora de elegir qué función hay que integrar y cuál hay que derivar.
¿Cómo elegir f’ y g?
Normalmente, se elige f’ la función que es más fácil integrar y dejamos la g para derivar, ya que derivar una función es más fácil que integrarla.
Son buenas candidatas a ser la función a integrar f’:
- Función del número e elevado a x
- Funciones trigonométricas: cos x, sen x…
- Funciones potenciales: x², x³, etc…
- El propio dx
Cuando coinciden varias de estas funciones en la integral, siempre elige la función a integrar en el orden de prioridad en el que están en el anterior listado, es decir, si tenemos esta integral:
La función a integrar será la de e elevado a x y la función cos x será la función a derivar:
El diferencial de x dx, siempre debe estar en la función derivada.
Por otro lado, la función ln x nunca podrá ser f’, ya que para integrar esa función, hay que utilizar el método de integración por partes.
Las funciones trigonométricas inversas (arc sen, arc cos, arc tag) tampoco pueden ser tampoco la función a integrar f’.
¿Qué pasa si no elijo bien f’ y g?
Si no eliges bien la función a integrar y a derivar, cada vez la integral será más complicada, por tanto, debes parar y cambiar tu elección.
Recuerda que tu objetivo es llegar a una integrar que se pueda resolver por integrales inmediatas y que te permita por tanto llegar a la solución de la integral.
Ejercicios resueltos de integración por partes
Hasta ahora, puede que todo lo que te he contado te sea difícil de asimilar, pero no te preocupes. Vamos a asentar conceptos resolviendo unas cuantas integrales por el método de integración por partes, en las que te explicaré cada uno de los pasos y entenderás mejor el funcionamiento de este método.
Te recomiendo que una vez termines de estudiar los ejercicios, vuelvas a leer la teoría anterior para que lo entiendas todo mucho mejor.
Todas estas integrales tienen algo en común y es que no es posible resolverlas con el método de integrales inmediatas, ya que no tienen la misma forma que ninguna de ellas ni tampoco se pueden retocar para que la tengan.
Por tanto, partiremos ya de esa base. Tenlo en cuenta.
Ejercicio resuelto 1
En primer lugar, sacamos fuera la constante:
Tenemos que elegir una función para integrar y otra para derivar. Como función para integrar, elegimos el cos x, ya que está por encima en la lista de prioridad. Dejamos como función para derivar la x:
Integramos f’ y derivamos g:
Date cuenta que siempre dx va con las derivadas.
Ahora ya tenemos todo lo que necesitamos (f, g, f’ y g’) para aplicar la fórmula de la integración por partes:
Por lo que las sustituimos por sus correspondientes funciones:
Nos queda por resolver una integral, que se resuelve por integrales inmediatas:
Finalmente operamos y añadimos la constante:
Ejercicio resuelto 2
Elegimos la función a derivar y la función a integrar:
En este caso, es sencillo, porque ln x nunca puede ser la función a integrar, por lo que no queda más remedio que sea la función a derivar.
Integramos f’ y derivamos g:
Aplicamos la fórmula de integración por partes:
En la integral que nos ha quedado, sacamos fuera la constante y operamos:
Nos queda una integral inmediata que pasamos a resolver:
Finalmente, operamos en el segundo término y añadimos la constante:
Ejercicio resuelto 3
En este caso, tenemos dos funciones candidatas a ser la función a integrar. Elegimos cos x por estar más arriba en el orden de prioridad y dejamos la otra función para derivar:
Integramos f’ y derivamos g:
Aplicamos la fórmula de integración por partes:
En la integral que nos queda, sacamos fuera la constante:
Nos ha vuelto a quedar una integral que no es posible resolverla por medio de integrales inmediatas, por lo que tenemos que volver a resolverla por partes. Seguimos el mismo criterio que antes para elegir la función a integrar y la función a derivar:
Integramos f’ y derivamos g:
Aplicamos nuevamente la fórmula de la integración por partes:
Sacamos fuera de la integral el signo menos, que es equivalente a tener un -1 y por tanto es una constante:
Esta vez la integral que nos queda sí se puede resolver por integrales inmediatas, por lo que pasamos a resolverla:
Operamos para eliminar los corchetes y añadimos la constante C:
Ejercicio resuelto 4
A simple vista, esta integral puede parecer que podría resolverse con una integral inmediata, sin embargo no es así.
Hay que resolverla por partes, pero parece que sólo tiene una función y eso puede causar confusión. No obstante, dx también puede utilizarse como función a integrar o a derivar ya que corresponde a la función derivada de x.
Por tanto, elegimos dx como función a integrar y el ln x como función a derivar. Además, todo cuadra porque ln x no puede elegirse para la función a integrar:
Integramos f’ y derivamos g:
Aplicamos la fórmula de integración por partes:
Operamos dentro de la integral que tenemos y nos queda:
Resolvemos la integral y añadimos la constante:
Ejercicio resuelto 5
Esta integral es un caso similar a la anterior. Elegimos como función a integrar el diferencial de x y el arc sen x como función a derivar:
Integramos f’ y derivamos g:
Aplicamos la fórmula de integración por partes:
La integral que nos queda se resuelve por medio de la integral inmediata de la función potencial compuesta, ya que tenemos una función elevada a un exponente (la raíz) y podríamos tener la derivada de esa función, donde la función es:
Y su derivada:
Le añadimos el 2 que le falta para que aparezca la derivada y dividimos la integral entre 2:
Ahora aplicamos la fórmula de la integral inmediata de la función potencial compuesta:
Operamos en el segundo término y añadimos la constante:
Integrales cíclicas en la integración por partes
Como has visto en los ejercicios anteriores, al ser el método de integración por partes un proceso iterativo, a veces es necesario volver a aplicar el método en las nuevas integrales que van surgiendo.
Puede darse el caso de que la nueva integral que surja, sea igual que la integral original, por lo que si seguimos aplicando el mismo procedimiento, entraríamos en un proceso cíclico infinito y no terminaríamos nunca de resolverla.
Vamos a ver un par de ejemplos de estas integrales al mismo tiempo que te explico el procedimiento para resolverlas:
Elegimos la función a integrar la función trigonométrica y la función exponencial como la función a derivar:
Integramos f’ y derivamos g:
Aplicamos la fórmula de integración por partes:
Sacamos fuera de la nueva integral el ln 2 por ser una constante:
La integral que queda, se vuelve a resolver por partes. Seguimos el mismo criterio para elegir f’ y g:
Integramos f’ y derivamos g:
Volvemos a aplicar la fórmula de integración por partes en la nueva integral:
Sacamos fuera de la integral que nos queda el ln 2:
Y si te das cuenta en este punto del ejercicio, vuelvo a repetir el paso anterior pero resaltando la integral que nos queda:
¿Te suena?
Efectivamente, es la integral original que estamos resolviendo.
¿Qué hacemos ahora?
Si seguimos igual, no terminaremos nunca, pero hay una solución.
A la integral original vamos a llamarle I:
Por tanto, todo el desarrollo que tenemos hasta ahora es igual a I y además, la integral que aparece dentro del desarrollo también es igual a I, por lo que la sustituimos por esta variable:
Ahora lo que tenemos es una ecuación donde la incógnita es I y hay que despejarla.
En primer lugar, multiplicamos ln 2 por los términos que están dentro del corchete para eliminarlo:
Ahora pasamos el término con I sumando al primer miembro:
En el primer miembro, sacamos factor común a la I:
Y finalmente, pasamos dividiendo el contenido del corchete que multiplica a la I y le añadimos la constante:
Ejemplo 2
En primer lugar, el denominador x, lo indicamos como una multiplicación por 1/x, para que se vea más claro que tenemos una multiplicación de dos funciones:
Elegimos la función a integrar la función 1/x y la función logarítmica como la función a derivar:
Integramos f’ y derivamos g:
Aplicamos la fórmula de integración por partes:
Operamos en el primer término multiplicando los logaritmos y en la integral, sacamos fuera el 2 y también multiplicamos los logaritmos:
Nos queda una integral que es igual a la integral original, que le llamamos I:
Por lo que tenemos:
Pasamos -2I al primer término:
Y finalmente despejamos I y le añadimos la constante:
Como ves, para saber cuándo se aplica el método de integración por partes, debes identificar una posible función para integrar y otra para derivar, siempre y cuando no sea posible resolverla con integrales inmediatas.
Si quieres aprender a integrar con todos los métodos, te recomiendo el Curso de Integrales Indefinidas.
¿Necesitas clases de matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más:

Exámenes resueltos de Matemáticas II Selectividad (EAU) País Vasco

Exámenes resueltos de Matemáticas II Selectividad (EBAU) Murcia

Exámenes resueltos de Matemáticas II Selectividad (EBAU) Extremadura

Exámenes resueltos de Matemáticas II Selectividad (EBAU) Castilla y León

Exámenes resueltos de Matemáticas II Selectividad (PAU) Valencia

Exámenes resueltos de Matemáticas II Selectividad (EBAU) Canarias

Exámenes resueltos de Matemáticas II Selectividad (EBAU) Asturias