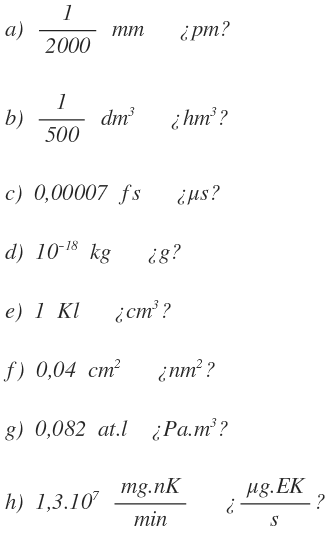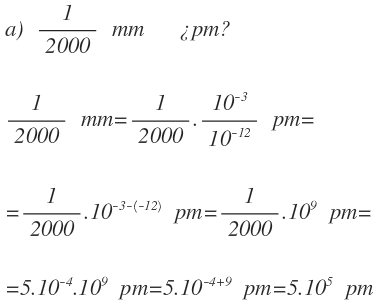A continuación te voy a explicar qué son los múltiplos y submúltiplos de una unidad de medida, para qué se utilizan y como convertir de una unidad a otra. Todo ello, con ejercicios resueltos paso a paso.
Si has llegado hasta aquí es porque buscas ayuda para resolver algún problema de física y necesitas clases de física online y es muy probable que también necesites refuerzo en matemáticas. Si después de leer esto, quieres seguir aprendiendo paso a paso, en una plataforma donde tengas todo explicado, con ejercicios resueltos y alguien que te resuelva tus dudas, solo tienes que apuntarte a los Cursos de Física Online:
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas y física. Puedo explicarte paso a paso cualquier duda que no entiendas.
Sólo tienes que dejarte guiar y verás como vas a aprendiendo poco a poco a resolver tus problemas de física
Múltiplos y submúltiplos
Vamos a empezar explicando qué son los múltiplos y los submúltiplos y para que se utilizan.
Los múltiplos y los submúltiplos son prefijos que se añaden a las unidades de medida para expresar su valor en una cifra que se pueda leer más fácilmente.
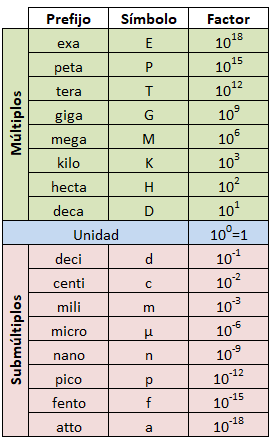
En la siguiente tabla te muestro los múltiplos y los submúltiplos, con el prefijo, el símbolo y el factor de conversión de cada uno:
Los múltiplos que aparecen en la tabla son deca, hecta, kilo, mega, giga, tera, peta y exa. Los submútliplos son deci, centi, mili, micro, nano, pico, fento y atto.
La primera columna corresponde con el prefijo que añadimos a la unidad de medida a la hora de escribirlo o hablarlo y la segunda columna al símbolo que añadimos cuando utilizamos el diminutivo de la unidad.
Además tenemos el factor de conversión, que corresponde con el valor del múltiplo o el submúltiplo con respecto a la unidad, es decir, cuántas veces es más grande o más pequeño ese múltiplo o ese submúltiplo que la unidad. Se expresa en potencias de 10, ya que así es más fácil la representación del valor, así como operar con ellos a la hora de convertir unidades.
Por ejemplo, que kilo sea 10³, significa que es igual a 1000 unidades. Si hablamos en longitud, 1 km es igual a 1000 metros (10³ metros).
De la misma forma, que el factor de micro sea 10 elevado a -6, significa que un micro son 0,000001 unidades. Si lo aplicamos al tiempo 1 microsegundo equivale a 0,000001 segundos.
Para poder trabajar con los factores de los múltiplos y los submúltiplos, es necesario que domines tanto las propiedades de las potencias, así como saber expresar cantidades en notación científica, lo que supone saber modificar el exponente de la potencia de 10, sin variar el resultado.
Cómo expresar las unidades con múltiplos y submúltiplos
Vamos a ver cómo expresar las unidades con el múltiplo o el submúltiplo más adecuando.
En primer lugar, expresamos la cifra en notación científica, si no está expresada en potencia de 10. Si ya está expresada en potencia de 10 (aunque no esté expresado notación científica correctamente), pasamos al siguiente paso.
El siguiente paso es buscar que el exponente de la potencia de 10 coincida con el factor del múltiplo o el submúltiplo más cercano.
Y por último, cambiar a la unidad que corresponda por su factor y eliminar la potencia de 10.
Por ejemplo, tenemos la siguiente medida:
No la tenemos expresada en potencia de 10, por lo que la pasamos a notación científica:
El factor que nos queda está muy cercano a 10^-3, por lo que trasformamos el exponente de -4 a -3 y al hacerlo, como la hemos hecho 10 veces más grande, el número que está delante de la potencia hay que hacerlo 10 veces más pequeño. Nos queda:
Finalmente, eliminamos la potencia de 10 y añadimos el prefijo que corresponde a la unidad de medida. Como en este caso 10^-3 corresponde a mili, lo quitamos y le añadimos la m de mili a la unidad de medida.
Por tanto, 0,00038 s lo expresamos más correctamente como 0,38 ms.
Vamos a ver otro ejemplo:
Ya tenemos la cifra expresada en potencia de 10, por lo que ahora tenemos que buscar a qué factor está más cerca. El factor que más cerca tiene es 10^9, por lo que cambiamos el exponente de 8 a 9 y al hacerlo, como al potencia la hemos hecho 10 veces más grande, el número que tiene delante lo hacemos 10 veces más pequeño para no variar su resultado. Nos queda:
Finalmente, eliminamos la potencia de 10 y lo sustituimos en la unidad de medida por el prefijo que corresponda a ese factor, que en este caso 10^9 corresponde con Giga:
Conversión de unidades con múltiplos y submúltiplos
Vamos a ver ahora cómo convertir de unidades pasando de unos prefijos a otros o incluso a la unidad de medida sin prefijo alguno. Para ello trabajaremos con los factores de conversión de los múltiplos o submúltiplos, por los que tienes que aprendértelos o tenerlos muy a mano.
Cómo pasar de unidades con prefijo a unidades sin prefijo
Empezaré explicando cómo pasar una unidad con prefijo (de múltiplo o de submúltiplo) a la unidad sin prefijo. Por ejemplo, vamos a pasar 4,26 mm a m:
Gracias a su factor de conversión, sabemos que 1 mm corresponde a 10 elevado a -3 m, por lo que podemos hacerlo con una regla de tres:
Despejando la x nos queda:
Si te das cuenta, la cantidad que teníamos inicialmente, queda multiplicada por el factor de conversión de la unidad inicial con prefijo:
Por lo que para pasar de unidades con prefijo a unidades sin prefijo, podemos aplicar la siguiente fórmula:
Es decir, la cantidad con prefijo se multiplica por su factor de conversión para obtener la cantidad en unidad sin prefijo.
Vamos a ver otro ejemplo donde apliquemos directamente lo que te acabo de explicar. Vamos a pasar 8500 kg a g:
Para pasar de kg a g multiplicamos la cifra por el factor de conversión de kilo, es decir, por 10³:
Y por último, lo expresamos en notación científica:
Cómo pasar de unidades sin prefijo a unidades con prefijo
¿Cómo lo hacemos si queremos pasar una unidad sin prefijo a una unidad con prefijo?
Vamos a verlo con el siguiente ejemplo. Vamos a pasar 26 litros a centilitros:
Al igual que antes, por el factor de conversión de centi, sabemos que 1 cl corresponde a 10 elevado a -2 litros, por lo que podemos utilizar una regla de tres:
Despejando la x nos queda:
Como puedes observar, la cantidad sin prefijo, al pasarla a una unidad con prefijo queda dividida por el factor de conversión de la unidad con prefijo:
Por lo que para pasar de unidades sin prefijo a unidades con prefijo, podemos aplicar la siguiente fórmula:
Y ahora ya dejamos el resultado en notación científica
Como la potencia nos queda con exponente negativo, lo pasamos a positivo:
Y finalmente lo expresamos correctamente en notación científica:
Vamos a ver otro ejemplo donde apliquemos directamente la fórmula. Vamos a pasar 3,8 A a μA:
Para pasar de A a μA dividimos la cifra entre el factor de conversión de micro, es decir, por 10 elevado a -6:
Ahora pasamos la potencia de 10 a exponente positivo, subiéndola al numerador
Y la dejamos así, ya que ya está expresada en notación científica.
Cómo pasar de una unidad cualquiera a otra con prefijo
Para pasar de una unidad con prefijo a otra unidad con prefijo, tendríamos que hacer dos reglas de tres, una para pasar a la unidad inicial con prefijo a la unidad sin prefijo y otra para pasarla de la unidad sin prefijo a la unidad final con prefijo.
Afortunadamente podemos aplicar la siguiente fórmula que nos ahorra mucho tiempo al evitar tener que realizar esas dos reglas de tres:
La fórmula consiste en multiplicar la cantidad con la unidad inicial por el factor de la unidad inicial y dividirlo entre el factor de la unidad final. El resultado estará expresado en la unidad final.
Realmente, esta fórmula se obtiene realizando las dos reglas de tres que te comentaba previamente, pero para no tener que realizarlas siempre y como el procedimiento siempre es el mismo, aplicaremos directamente esta fórmula. Aun así, es bueno que sepas cómo se obtiene esta fórmula.
De hecho, también la podemos aplicar cuando tengamos unidades sin prefijo en las cantidades inicial o final, tan sólo con poner 1 en el factor que corresponda.
Vamos a ver un ejemplo. Vamos a pasar 0,047 Ms a ks:
Aplicamos la fórmula multiplicando la cantidad por el factor de la unidad inicial, que en nuestro caso es Mega, por lo que multiplicamos por 10 elevado a 6 y dividimos entre el factor de la unidad final, que en nuestro caso es kilo, por lo que dividimos entre 10³:
Ahora dividimos las potencias, manteniendo la base y restando los exponentes:
Y por último expresamos el resultado en notación científica:
Cómo convertir unidades elevadas al cuadrado o al cubo
¿Cómo realizamos la conversión de unidades cuando están elevadas al cuadrado o al cubo?
Para pasar unidades que estén elevadas al cuadrado o al cubo, el procedimiento es exactamente el mismo, solo que hay que elevar los factores de conversión al cuadrado o al cubo, y luego realizar las operaciones correspondientes con las potencias de 10 para llegar al resultado final.
Por ejemplo vamos a pasar 0,4 m² a mm²:
Para pasar de m² a mm² dividimos los 0,04 entre el factor de mili, elevado al cuadrado:
Eliminamos el paréntesis de la potencia multiplicando los exponentes:
Pasamos el exponente a positivo subiendo la potencia al numerador:
Y expresamos el resultado en notación científica:
Vamos a ver otro ejemplo con unidades cúbicas:
Multiplicamos la cantidad por el factor de mili elevado al cubo:
Eliminamos el paréntesis de la potencia multiplicando los exponentes:
Expresamos la fracción como potencia de 10:
Multiplicamos las potencias de 10 manteniendo la base y sumando los exponentes, quedando el resultado en notación científica:
Cómo convertir unidades si tenemos más de una unidad y en una fracción
Se puede dar el caso que la cantidad se mida con varias unidades y que se exprese en forma de fracción, como por ejemplo la velocidad, que se mide en espacio entre tiempo. ¿Cómo pasar de unas unidades a otras en este caso?
Vamos a verlo con un ejemplo. Vamos a pasar de km/h a m/s:
En estos casos, debemos realizar el cambio de unidades en el numerador por un lado y en el denominador por el otro, es decir, hay que realizar dos cambios de unidades independientes.
En el numerador, debemos pasar de km a m. Sabemos que 1 km son 10³ m, por el factor de conversión, luego en el numerador, multiplicamos por 10³:
Por otro lado, en el denominador, debemos pasar de h a s. Sabemos que 1 hora son 3600 segundos, por lo que para pasar de horas a segundos se multiplica por 3600, pero en el denominador
Por tanto, la cantidad queda multiplicada por 10³ y dividida entre 3600 (aunque en el denominador hayamos multiplicado por 3600, al estar en el denominador, queda dividiendo a 10³):
Finalmente operamos con la calculadora y nos queda:
Vamos a ver otro ejemplo para que queda más claro. Vamos a pasar de MN/km² a mN/m²:
En el numerador, pasamos de MN a mN multiplicando por el factor de Mega, que es 10 elevado a 6 y dividiendo entre el factor de mili, que es 10 elevado a -3:
En el denominador, pasamos de km² a m² multiplicando por el factor de kilo, elevado al cuadrado:
Finalmente, la cantidad queda multiplicada por el factor resultante del numerador y dividida entre el factor resultante del denominador:
Operamos con potencias de 10 manteniendo la base y restando los exponentes:
Y expresamos el resultado en notación científica:
Ejercicios resueltos de conversión de unidades
Vamos a aplicar lo aprendido hasta ahora con resolviendo unos ejercicios de conversión de unidades paso a paso.
Ejercicio 1
Realiza los siguientes cambios de unidad:
Apartado a:
Multiplicamos los 200 fs por el factor de fento, que es 10 elevado a -15 y dividimos entre el factor de la unidad, que es 10 elevado a 0 (o entre 1):
Dividimos potencias manteniendo la base y restando los exponentes:
Y pasamos el resultado a la forma exponencial:
Apartado b:
Multiplicamos los 50 μA por el factor de micro, que es 10 elevado a -6 y dividimos entre el factor de la unidad, que es 10 elevado a 0 (o entre 1):
Dividimos potencias manteniendo la base y restando los exponentes:
Y pasamos el resultado a la forma exponencial:
Apartado c:
Multiplicamos la cantidad por el factor de pico, que es 10 elevado a -12 y dividimos entre el factor de Giga, que es 10 elevado a 9:
Operamos con las potencias de 10, manteniendo la base y sumando o retando exponentes según esté multiplicando o dividiendo la potencia:
El resultado ya queda expresado en notación científica.
Apartado d:
Multiplicamos la cantidad por el factor de Mega, que es 10 elevado a 6 y dividimos entre el factor de atto, que es 10 elevado a -18:
Dividimos potencias manteniendo la base y restando los exponentes:
Finalmente, expresamos la fracción como una potencia de 10 y la multiplicamos por la otra potencia de 10, manteniendo la base y sumando los exponentes:
El resultado ya queda expresado en notación científica.
Apartado e:
Multiplicamos la cantidad por el factor de mili, que es 10 elevado a -3 y dividimos entre el factor de Pico, que es 10 elevado a 15:
Operamos con las potencias de 10, manteniendo la base y sumando o retando exponentes según esté multiplicando o dividiendo la potencia:
El resultado ya queda expresado en notación científica.
Ejercicio 2
Expresa las siguientes cantidades utilizando múltiplos y submúltiplos de la unidad más adecuada:
Apartado a:
Expresamos la cifra en notación científica:
Nos queda directamente el factor de micro, por lo que eliminamos el factor y expresamos el resultado en microNewtons:
Apartado b:
Ya tenemos la cifra expresada en potencias de 10.
El factor más cercano a 10 elevado a 7 es 10 elevado a 6, que es el factor de Mega, por lo que cambiamos el exponente a 6 y como hemos hecho la potencia 10 veces más pequeña, hacemos el número que tiene delante 10 veces mayor:
Eliminamos el factor y expresamos el resultado en Megagramos:
Apartado c:
Ya tenemos la cifra expresada en potencias de 10.
El factor más cercano a 10 elevado a -4 es 10 elevado a -3, que es el factor de mili, por lo que cambiamos el exponente a -3 y como hemos hecho la potencia 10 veces más grande, hacemos el número que tiene delante 10 veces menos:
Finalmente, expresamos el resultado en mA, eliminando el factor:
Ejercicios propuestos
Ejercicio 1
Expresa las siguientes cantidades utilizando múltiplos y submúltiplos de la unidad más adecuada:
Ejercicio 2
Realiza los siguientes cambios de unidad:
¿Necesitas ayuda en física y matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para entender física y las matemáticas que necesitas aplicar.
He diseñado un método práctico y efectivo que te ayudará a entender la física así como las matemáticas que necesitas aplicar, paso a paso, explicándote justo lo que necesitas para saber resolver todos problemas y saber aplicar las fórmulas que correspondan. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus problemas de física
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando información por Internet si puedes aprenderlo en menos de 20 minutos?
Te explicaré lo que necesitas aprender para entender física y las matemáticas que necesitas aplicar. ¿Quieres informarte de como puedes aprender física y matemáticas? Pulsa el botón para saber más: