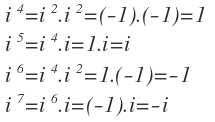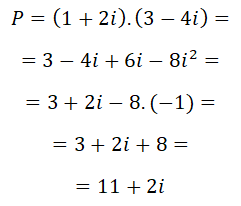A continuación te voy a explicar cómo operar con números complejos cuando están expresados en forma binómica, con ejemplos y ejercicios resueltos paso a paso.
Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Suma y resta de números complejos
La suma o resta de números complejos se realiza sumando o restando las partes reales de los números complejos por un lado y las partes imaginarias por otro.
En general, si tenemos dos números complejos:
El resultado de sumarlos o restarlos será otro número complejo cuya parte real es la suma o resta de la parte real de cada número complejo y su parte imaginaria es la suma o resta de la parte imaginaria de cada número complejo:
Por ejemplo, vamos a realizar la suma y resta de los siguientes números complejos:
En primer lugar eliminamos los paréntesis, teniendo en cuenta el signo que tienen delante:
Ahora sumamos y restamos por un lado las partes reales y por otro las partes imaginarias. El resultado es:
Multiplicación de números complejos en forma binómica
La multiplicación de números complejos en forma binómica se realiza igual que la multiplicación de polinomios, cuando tenemos un polinomio por un polinomio, es decir, se multiplica cada término del número complejo, por los otros dos términos del otro número complejo, ya que realmente estamos multiplicando dos binomios.
Lo único que hay que tener en cuenta que cuando tengamos i², hay que sustituirlo por -1, ya que si por definición, i es igual a la raíz de -1, entonces, i al cuadrado es -1:
Vamos a ver un ejemplo de cómo multiplicar dos números complejos en forma binómica:
Multiplicamos el primer término del primer número complejo, por ambos términos del segundo número complejo y después hacemos lo mismo con el segundo término del primer número complejo, siempre teniendo en cuenta la regla de los signos. Nos queda:
Ahora sustituimos i² por -1:
Realizamos la multiplicación de -1 por el número que teníamos delante, que en este caso es -12:
Finalmente, sumamos los números complejos que nos quedan, por un lado las partes reales y por otro las partes imaginarias:
División de números complejos en forma binómica
Para dividir dos números complejos en forma binómica, hay que multiplicar el numerador y el denominador por el conjugado del denominador.
Después realizamos las multiplicaciones resultantes y finalmente, separamos el resultado en una parte real y en otra imaginaria.
Vamos a verlo más despacio con el siguiente ejemplo:
Multiplicamos el numerador y el denominador por el conjugado del denominador, que lo obtenemos cambiando de signo la parte imaginaria:
Realizamos la multiplicación tanto en el numerador como en el denominador. En el denominador nos queda una suma por diferencia:
Resolvemos los cuadrados del denominador:
Sustituimos i² por -1:
Operamos en los términos donde tengamos que multiplicar por -1:
Sumamos y restamos tanto en el numerador como en el denominador. En el numerador sumamos por un lado la parte real y por otro la parte imaginaria. En el denominador solamente tenemos parte real:
Finlamente, separamos la fracción en dos términos, uno correspondiente a la parte real y otro correspondiente a la parte imaginaria:
Inverso de un número complejo en forma binómica
En general, el inverso de un número cualquiera «n» es igual a 1 partido por ese mismo número:
Por tanto, el inverso de un número complejo se obtiene de la misma forma, sólo que en este caso el número tiene parte real e imaginaria (a+bi):
Para volver a dejar el número complejo en forma binómica (a+bi), hay que realizar la división.
Vamos a verlo con un ejemplo: Vamos a obtener el inverso del siguiente número complejo:
En primer lugar, empezamos dividiendo 1 entre el número complejo:
Ahora tenemos que realizar la división. Como es una división de números complejos, multiplicamos numerador y denominador por el conjugado del denominador:
Operamos en el numerador y en el denominador:
Resolvemos las potencias del denominador:
Sustituimos i² por -1 y operamos:
Por último, separamos el resultado en la parte real y en la parte imaginaria:
Y ahora sí, este es el inverso del número complejo anterior.
Potencia de un número complejo en forma binómica
Vamos a ver cómo realizar la potencia de un número complejo en forma binómica, es decir, un número complejo elevado a un número n:
La potencia de un número complejo en forma binómica se realiza de la misma forma que se resolvería una potencia en un binomio (polinomio de dos términos).
Por ejemplo, para resolver el cuadrado de un número complejo, lo haríamos mediante los productos notables.
Por ejemplo:
En este caso se trata del cuadrado de una diferencia, por lo que aplicamos su fórmula correspondiente:
Operamos:
Sustituimos i² por -1 y operamos:
Finalmente sumamos la parte real y queda:
Si el exponente al que queda elevado el número complejo es mayor a 2, no queda más remedio que multiplicar el número complejo tantas veces como indique el exponente, igual que una multiplicación de polinomios.
Potencias de i
En las potencias de números complejos, hay que tener en cuenta las potencias de i, ya que su valor variará en función de su exponente.
Si i está elevado a 0, 1 o 2, su resultado es sencillo:
El resto de potencias de i, se puede calcular a partir de éstas. Por ejemplo, para calcular i elevado a 3 sería:
De la misma forma, se pueden ir calculando cualquier potencia de i. Si seguimos calculando potencias nos queda:
Observa que desde i elevado a 0, hasta i elevado a 3, los valores son 1, i, -1 y -i. Desde i elevado a 4 hasta i elevado a 7, esos resultados se vuelven a repetir. Es decir, los resultados de las potencias de i se van repitiendo de cuatro en cuatro, siendo 1, i, -1 y -i.
Si seguimos calculando potencias, vemos como efectivamente se siguen repitiendo:
¿Qué pasa si tenemos un exponente más alto?
No podemos ir calculando potencias sucesivas hasta llegar. Lo que hay que hacer es aprovecharnos de que los valores de las potencias se van repitiendo.
Vamos a ver un ejemplo: Calcular el valor de i elevado a 40:
Todos las potencias de i cuyo exponente sea múltiplo de 4, su resultado es 1 (i elevado a 0, i elevado a 4, i elevado a 8…).
En este caso, 40 es múltiplo de 4, por tanto su resultado es 1, ya que lo podemos resolver de la siguiente manera:
Vamos a ver otro ejemplo:
En este caso, 18 lo podemos poner como 16 (que es el múltiplo de 4 más cercano a 18) más 2 y gracias a las propiedades de las potencias, lo podemos resolver como:
Afortunadamente, existe un método mucho más directo, que nos sirve para resolver potencias de i de cualquier exponente, por muy alto que sea. Vamos a verlo con un ejemplo:
Como hemos dicho antes, sabemos que las potencias de i cuyo exponente sea múltiplo de 4, va a tener como resultado 1.
Por tanto, vamos a dividir el exponente entre 4:
El dividendo de una división lo podemos expresar como:
Por tanto, en nuestro caso, 419 será:
Esta expresión la colocamos como exponente:
Separamos la potencia en una multiplicación de potencias, ya que según las propiedades de las potencias, una suma de exponentes equivale a una multiplicación de potencias:
Ahora, la primera potencia, es igual a 1, al ser múltiplo de 4, por lo que sólo tengo que resolver la segunda potencia:
Que se resuelve conociendo los valores de las primeras potencias:
Si necesitas seguir aprendiendo sobre números complejos te recomiendo el Curso de Números Complejos, donde también te explico cómo pasar un número complejo de forma binómica a polar y ha realizar operaciones con números complejos en forma polar. Con ejercicios resueltos paso a paso.
Ejercicios resueltos de operaciones con números complejos en forma binómica
Ejercicio 1
Obtener polinomios cuyas raíces sean:
Este ejercicio se resuelve a partir de las propiedades de una ecuación de segundo grado, explicadas en esta lección, con las que podemos obtener la ecuación de segundo grado a partir de conocer sus soluciones. Te recomiendo que le eches un vistazo a la lección para que entiendas mejor esta resolución.
Conocidas las soluciones o raíces de una ecuación de segundo grado, podemos expresar la ecuación así, en la llamada forma canónica:
Donde S es la suma de las soluciones:
Y P es el producto de las soluciones:
Ahora vamos a resolver el ejercicio aplicando lo que acabamos de ver.
Apartado a:
Las dos soluciones son:
Calculamos la suma:
Calculamos el producto:
Y sustituimos S y P en la forma canónica de la ecuación de segundo grado:
Apartado b:
Las dos raíces son:
Obtenemos el valor de S:
Obtenemos P:
Sustituimos S y P en la ecuación:
Apartado c:
Ahora las soluciones son:
Calculamos S:
Obtenemos P:
Sustituimos S y P:
En este caso, los coeficientes de la ecuación son números complejos.
Ejercicio 2
¿Cuánto debe valer x en el siguiente número complejo para que sea imaginario puro?
En primer lugar desarrollamos el número complejo como el cuadrado de una resta:
Resolvemos el cuadrado del tercer término:
Sustituimos i² por -1:
Operamos en el tercer término:
Agrupamos los términos que corresponden a la parte real:
Para que el número complejo sea imaginario puro, la parte real debe ser igual a 0. Por tanto, igualamos la parte real a 0:
En la ecuación que obtenemos, despejamos x²:
Y finalmente despejamos x:
¿Necesitas ayuda con las matemáticas? ¿Quieres que te explique cualquier duda que te surja paso a paso?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: