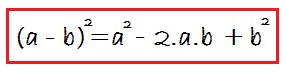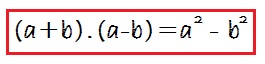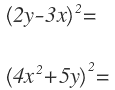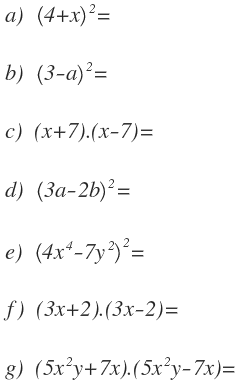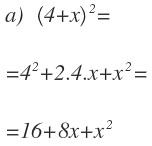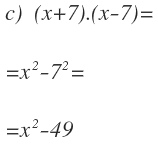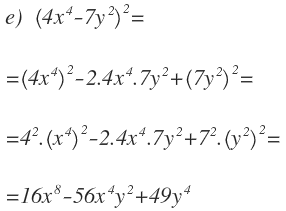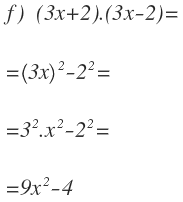Aqui vou explicar-vos o que são produtos notáveis, também conhecidos como identidades notáveis. Veremos as fórmulas de cada uma delas e as aplicaremos por meio de exercícios resolvidos passo a passo.
Vou explicar passo a passo as diferentes fórmulas dos produtos notáveis, com exemplos resolvidos passo a passo, para que você aprenda a aplicá-las.
O que são produtos ou identidades notáveis
O que são produtos notáveis?
Produtos notáveis, também chamados de identidades notáveis, são polinômios de dois termos (binômios) ao quadrado, ou o produto de dois binômios, como veremos abaixo, cujo desenvolvimento sempre segue as mesmas regras.
Multiplicar dois polinômios entre si, se tiverem mais de três termos, pode ser muito entediante e você pode gastar muito tempo fazendo a multiplicação. As fórmulas dos produtos notáveis, que te permitirão realizar a multiplicação diretamente, sem ter que ir de termo a termo.
Quadrado binomial
Para que conste, vamos ver o que é um binómio quadrado.
Como eu mencionei antes, um binômio é um polinômio de dois termos, que pode ser adicionado ou subtraído:
Podemos multiplicar estes binómios um com o outro de três maneiras diferentes:
Uma soma por uma soma:
Uma diferença para uma diferença:
E uma soma por uma diferença:
Os dois primeiros casos podem ser quadrados como binômios, já que o mesmo binômio está sendo multiplicado duas vezes:
Fórmulas de Produtos Notáveis
As fórmulas dos produtos mais notáveis são: o quadrado de uma adição, o quadrado de uma subtracção e a adição por diferença ou diferença de quadrados.
Vamos dar uma olhada em cada um deles:
Sum Square Formula
Começamos com a multiplicação de duas binômios em que seus termos (iguais em ambas as binômios) estão sendo adicionados juntos:
Estamos a multiplicar o mesmo binómio duas vezes, por isso podemos colocá-lo como o quadrado de uma soma:
Por outro lado, se multiplicarmos os dois binómios que temos:
E reagrupamento de termos:
Este produto notável é lido: Quadrado do primeiro, mais o dobro do primeiro pelo segundo, mais o quadrado do segundo: 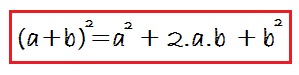
O primeiro é «a» (o primeiro termo do polinômio) e o segundo é «b» (o segundo termo do polinômio):
Para aplicar esta fórmula você só precisa substituir os termos do polinômio por a e b. Por exemplo:
Este é o quadrado de uma soma e vamos aplicar a sua fórmula para não termos de fazer a multiplicação.
O primeiro é x e o segundo é 1:
- Quadrado do primeiro: x²
- O dobro do primeiro pelo segundo: 2.x.1
- Segundo quadrado: 1²
Até agora você aplicou a fórmula. Agora temos que operar dentro de cada termo para simplificar, multiplicando números e poderes de resolução:
Um erro grave é não perceber que a expressão acima é um produto notável e enquadrar cada termo incorretamente:
Fórmula do quadrado de uma subtração ou quadrado de uma diferença
Esta fórmula é muito semelhante à anterior. É por isso que você deve ter muito cuidado para não confundi-los, pois eles só diferem em um sinal.
Neste caso, temos a multiplicação de dois binômios em que seus termos (iguais em ambos os binômios) estão sendo subtraídos:
Esta multiplicação, podemos colocá-la como o quadrado de uma subtracção:
Se fizermos a multiplicação dos binómios, conseguimos:
Chegamos à conclusão de que o quadrado de uma diferença é sempre igual:
É assim que se lê: Quadrado do primeiro, menos o dobro do primeiro para o segundo, mais o quadrado do segundo.
Como no caso anterior, o primeiro é «a» (o primeiro termo do polinômio) e o segundo é «b» (o segundo termo do polinômio):
Para aplicar esta fórmula você só precisa substituir os termos do polinômio por a e b.
Por exemplo:
Aplicamos a fórmula do quadrado de uma subtracção:
- Quadrado do primeiro: 2²
- O dobro do primeiro pelo segundo: 2.2.x
- Segundo quadrado: x²
Tanto o quadrado de uma adição quanto o quadrado de uma subtração podem ser utilizados para fatorar polinômios, aplicados em sentido inverso, ou seja, a partir do desenvolvimento, obtendo-se o produto notável.
Soma por Fórmula da Diferença: Diferença de Praças
A terceira das fórmulas que vamos ver é encontrar diretamente o resultado de uma soma por diferença de binômios:
Se desenvolvermos a multiplicação deles, já a temos:
Portanto, a soma por diferença será igual a:
Esta fórmula é muito útil na fatorização de polinômios e na simplificação de frações algébricas quando temos a subtração de dois termos ao quadrado.
Vejamos um exemplo de como aplicar esta fórmula:
O primeiro é x e o segundo é 1, então:
- O quadrado do primeiro é: x²
- O quadrado do segundo: 1²=1
Portanto, a diferença de quadrados permanece:
Às vezes, como ao calcular o polinômio, esta fórmula é muito útil aplicada na direção oposta. Por exemplo:
O que temos que identificar nos polinômios deste tipo é se é ou não uma diferença de quadrados. À primeira vista, parece que não é porque o primeiro termo não é quadrado, mas sim porque podemos colocá-lo como 5²:
E agora é mais claro que é uma diferença de quadrados. Portanto, podemos colocá-lo como uma soma pela diferença:
Ter em conta com as fórmulas de produtos notáveis
Outra coisa a ter em mente é que o primeiro e segundo termos não precisam ser formados por um único fator. Cada termo pode ser composto de vários fatores, por exemplo:
Nesse caso, tenha muito cuidado e não se esqueça de quadrar todo o termo, com a aplicação da propriedade do poder correspondente.
Cubo de uma soma
O cubo de uma soma se resolve com a seguinte fórmula:
Vamos ver um exemplo:
Neste caso, substituímos 3x³ por «a» e 2x por «b»:
Operamos para resolver os parênteses, aplicando as propriedades dos poderes:
Finalmente, multiplicamos fatores e poderes em cada termo:
Cubo de diferença
Agora vamos ver como resolver o cubo de uma diferença. Neste caso, aplica-se a seguinte fórmula:
É muito semelhante ao cubo de uma soma, mas tem dois sinais a menos no segundo e quarto termos.
Por exemplo:
Neste caso «a» é 4x² e «b» é 7x. Substituímos «a» e «b» pelos seus valores na fórmula:
Primeiro resolvemos os parênteses:
Y por último multiplicamos factores e potências em cada término:
Trinomio al cuadrado
Um trinómio é um polinómio de três términos. A fórmula para resolver o quadrado de um trinômio é:
Por ejemplo:
Sustituimos «a», «b» e «c» por seus valores:
E operamos para simplificar términos:
Ejemplos de produtos notáveis com términos de vários factores
No siempre, el primer y el segundo término de un binomio tienen por qué estar formados por un sólo factor. Cada termo pode ser formado por vários fatores, como por exemplo, por exemplo:
Nestes casos, quando se fala em primeiro lugar e segundo mandato, é preciso ter em conta esta propriedade das potências:
Que dice que la cuando tenemos una multiplicación elevada a un exponente, el resultado es igual a cada factor elevado a ese mismo exponente.
Vamos resolver os produtos notáveis anteriores para que te quede tudo mais claro:
No primeiro lugar, identificamos os términos: o primeiro é 2y e o segundo 3x.
Aplicamos a fórmula do cuadrado de um resta e queda:
Ahora es cuando al elevar al cuadrado varios factores hay que aplicar esta propedad;
Y nos queda:
Por último, simplificamos términos, resolvendo potências e multiplicando números:
Vamos com o segundo ejemplo:
Esta vez é o cuadrado de uma suma. O primer término é 4x² e o segundo 5y.
Aplicamos a fórmula:
Esta vez, a hora de elevar o cuadrado, dentro do primeiro termo, tengo otro cuadrado, por tanto, recuerda que hay que multiplicar los exponentes:
Finalmente simplificamos cada término:
Vamos ver um tercer ejemplo com uma suma por diferença:
Aplicamos sua fórmula:
Resolvemos os problemas e simplificamos:
Ejercicios resueltos de produtos notáveis
1 – Realiza as seguintes identidades notáveis: