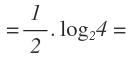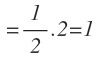¿Quieres aprender a aplicar las propiedades de los logaritmos? ¿Quieres saber cómo funcionan?
A continuación te voy a explicar cada una de las propiedades de los logaritmos. Lo interesante de las propiedades de los logaritmos no es sólo saberlas, sino saber aplicarlas en la resolución de ecuaciones logarítmicas.
Estudiaremos paso a paso, con todo detalle, todas las propiedades de los logaritmos, con ejemplos resueltos para que las comprendas mejor y empieces a saber cómo funcionan.
Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Propiedades de los logaritmos y ejemplos
Propiedad 1
El logaritmo en cualquier base de 1 es igual a 0:
Directamente, cuando veamos el logaritmo de 1, da igual la base que tenga, podemos sustituirla por un 0.
Por ejemplo:
Propiedad 2
Cuando en el logaritmo de un número, la base y el número son iguales, el resultado del logaritmo es 1:
Gracias a esta propiedad, podemos sustituir directamente un logaritmo con igual base e igual número por 1, si nos conviene para resolver ecuaciones:
Por ejemplo:
Propiedad 3
Cuando en el logaritmo de un número, la base y el número son iguales y el número está elevado a un exponente, el logaritmo será igual al exponente del número:
Esta propiedad es muy útil para convertir cualquier número en un logaritmo
Por ejemplo:
Con esta propiedad, también podemos calcular el valor de un logaritmo si es posible expresar el contenido del logaritmo como potencia de la misma base del logaritmo, como por ejemplo:
Escribimos el 81 en forma de potencias de 3:
Y directamente aplicando esta propiedad, vemos que el resultado es igual a 4.
Propiedad 4
El logaritmo en una base cualquiera de la multiplicación de dos números es igual a la suma de los logaritmos en esa misma base:
Por ejemplo para resolver un logaritmo de dos números multiplicándose:
Aplicamos la propiedad de la multiplicación:
Expresamos los números en forma de potencia:
Y aplicamos la propiedad 3 para resolver cada logaritmos y dar el resultado final:
Esta propiedad es una de la más utilizadas en la resolución de ecuaciones logarítmicas, ya que nos permite simplificar varios logaritmos en uno:
Propiedad 5
El logaritmo en una base cualquiera de la división de dos números es igual a la resta de los logaritmos en esa misma base:
Por ejemplo:
Aplicamos la propiedad de la división:
Expresamos los números en forma de potencia:
Y resolvemos los logaritmos aplicando la propiedad 3, ya que la base del logaritmo y la base de la potencia son iguales, llegando al resultado de la operación:
Junto con la propiedad anterior, permite simplificar varios logaritmos en uno sólo cuando estamos resolviendo ecuaciones logarítmicas:
Propiedad 6
Si tenemos un exponente en el logaritmo, ese exponente puede pasar a multiplicar al logaritmo:
Gracias a esta propiedad, podemos poner multiplicando el exponente, o colocar un número que multiplica al logaritmo como exponente según nos convenga.
Por ejemplo:
Aplicamos la propiedad poniendo el 6 multiplicando al logaritmo:
Ahora resolvemos el logaritmo sin el exponente, pasando el 512 a forma de potencia:
Calculamos el logaritmo aplicando la propiedad 3 y al final, multiplicamos los dos números que nos quedan:
Con esta propiedad, también podemos resolver los logaritmos de una raíz, como por ejemplo:
Ponemos la raíz en forma de potencia:
Y ahora el exponente lo colocamos delante del logaritmo multiplicando:
Ahora pasamos a resolver el logaritmo ya sin raíz. Ponemos el 4 en forma de potencia:
Resolvemos el logaritmo y lo multiplicamos por la fracción que teníamos delante:
Para resolver ecuaciones logarítmicas, conviene deshacernos de los números que están multiplicando a los logaritmos. Esta propiedad, nos permite hacerlo, pasando el número como exponente del logaritmo, como por ejemplo:
Ejercicio resuelto aplicando propiedades de los logaritmos
Ahora vamos a simplificar la siguiente expresión aplicando las propiedades:
En primer lugar aplicamos la propiedad de logaritmo de una división:
De esta forma, eliminamos la fracción dentro del logaritmo neperiano. Por tanto, nos queda el logaritmo neperiano del numerador, menos el logaritmo neperiano del denominador:
Nos han quedado dos logaritmos neperianos que se están restando. En cada uno de los logaritmos, aplicamos la propiedad de logaritmos de una multiplicación:
y de esta forma eliminados los productos dentro de los logaritmos neperianos.
Tanto en el primer como en el segundo término, nos queda un logaritmo neperiano por cada uno de los factores.
Date cuenta, que como delante del segundo término tenemos un signo menos, al aplicar la propiedad del logaritmo de una multiplicación, los dos logaritmos resultantes van encerrados entre paréntesis precedidos por ese signo menos:
Eliminamos el paréntesis cambiando el signo a los logaritmos neperianos que tiene dentro:
Y finalmente, en el primer logaritmo, aplicamos la propiedad de logaritmo de una potencia, para eliminar el exponente:
Nos queda:
Por tanto, hemos simplificado la expresión, al no tener dentro de los logaritmos ni potencias, ni productos, ni fracciones. Lo dejamos así ya que no podemos seguir operando ni aplicando ninguna propiedad más.
Aunque las propiedades de los logaritmos sean algo complejas de asimilar de forma aislada, cobran un mayor sentido cuando las apliquemos en la resolución de ecuaciones logarítmicas. Te lo explico más despacio en el Curso de Logaritmos.
¿Necesitas ayuda con las matemáticas? ¿Quieres que te explique cualquier duda que te surja paso a paso?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: