Proyecciones entre elementos del espacio. Ejercicios resueltos

A continuación te voy a explicar cómo obtener las proyecciones entre elementos del espacio, es decir, la proyección de un punto sobre un plano o una recta, así como la proyección de una recta sobre un plano.

Estas proyecciones se denominan proyecciones ortogonales, que consisten en realizar la proyección en la dirección perpendicular al elemento sobre el que se proyecta.

Si has llegado hasta aquí es porque necesitas un profesor de matemáticas online. Si después de leer esto, quieres que te ayude a entenderlas de verdad, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.

Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:

QUIERO APRENDER MATEMÁTICAS

Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.

¡Vamos a ver las más comunes!

Proyección de un punto sobre un plano

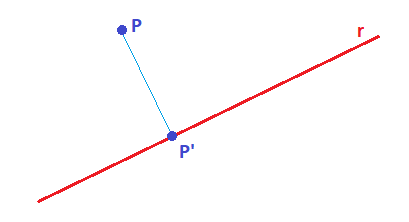
La proyección de un punto P sobre un plano es otro punto P’, que está contenido en el plano y es la intersección del plano con la recta que pasa por el punto P y es perpendicular el plano.

Conocer la proyección de un punto sobre un plano nos va a permitir calcular cosas como la distancia de un punto a un plano, el punto simétrico de un punto dado con respecto de un plano o el punto de un plano con menor distancia a otro.

Para obtener la proyección de un punto sobre un plano, en primer lugar hay que calcular la ecuación de la recta que pasa por el punto P y es perpendicular al plano, para lo cual necesitamos un punto (que es el punto P) y un vector de dirección (que es el vector normal del plano).

La ecuación de la recta debe estar en su forma implícita, para poder resolver el sistema que forman las dos ecuaciones de la recta con la ecuación del plano. La solución de este sistema serán las coordenadas de la proyección de P sobre el plano, es decir, del punto P’.

Vamos a ver un ejemplo:

Ejercicio resuelto sobre cálculo de la proyección de un punto sobre un plano

Calcular la proyección del punto P (1,2,3) sobre el plano 2x-y+3z+5=0:

Tenemos el siguiente punto:

Y queremos calcular su proyección sobre el siguiente plano:

Vamos a calcular la ecuación de la recta PP’, que es perpendicular al plano y pasa por el punto P:

Al ser la recta perpendicular al plano, su vector de dirección es igual al vector normal del plano:

Una vez tenemos el vector de dirección del plano y el punto P por donde pasa, podemos calcular la ecuación de la recta PP’. Obtendremos su ecuación en forma contínua, que es casi directo (tienes explicado cómo hacerlo en la lección de ecuaciones de la recta en el espacio):

Necesitamos las ecuaciones de la recta en su forma implícita, luego tenemos que pasar la ecuación contínua a las ecuaciones implícitas. Para ello, igualamos los términos de la igualdad dos a dos y nos quedan las siguientes dos ecuaciones:

Simplificamos ambas ecuaciones.

La primera ecuación:

Pasamos cada denominador al miembro contrario multiplicando:

Eliminamos paréntesis multiplicando por el número que llevan delante:

Reagrupamos términos y reordenamos:

Con la segunda ecuación hacemos lo mismo:

Pasamos los denominadores el miembro contrario:

Eliminamos paréntesis:

Reagrupamos y reordenamos términos:

Ambas ecuaciones simplificadas formas las ecuaciones implícitas de la recta PP’:

El punto P’ que estamos buscando, que es la proyección del punto P sobre el plano, es el punto de corte de la recta PP’ con el plano:

Para calcular el punto de corte P’, debemos resolver el sistema de ecuaciones formado por las ecuaciones implícitas de la recta y la ecuación del plano:

La solución de este sistema corresponderá con las coordenadas del punto P’.

La matriz de los coeficientes es:

Y la matriz ampliada:

Calculamos el determinante de la matriz de los coeficientes:

El determinante es distinto de cero, luego el rango de A es igual a 3:

Como A está contenida en A*, el rango de A* también es igual a 3:

Y como el rango de ambas matrices es igual a 3, que es igual al número de incógnitas, el sistema es compatible determinado y por tanto tiene solución y se puede resolver mediante la regla de Cramer, que lo tienes explicado paso a paso en el Curso de Determinantes:

La incógnita «x» es igual al determinante asociado a “x” entre el determinante de la matriz de los coeficientes:

La incógnita «y» es igual al determinante asociado a “y” entre el determinante de la matriz de los coeficientes:

La incógnita «z» es igual al determinante asociado a “y” entre el determinante de la matriz de los coeficientes:

Por tanto, las coordenadas del punto P’ son:

Que efectivamente, si sustituimos x, y y z por las coordenadas del punto en la ecuación del plano, vemos que se cumple la igualdad y por tanto el punto pertenece al plano:

Proyección de un punto sobre una recta

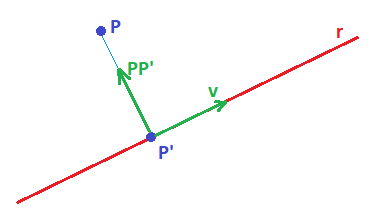
La proyección de un punto sobre una recta es el punto de corte entre esa recta y la recta perpendicular e ella que pasa por el punto P:

Como ambas rectas son perpendiculares, sus vectores de dirección también son perpendiculares:

Y por tanto, su producto escalar es igual a cero:

La proyección de un punto sobre una recta se calcula a partir de la condición de que el producto escalar de los vectores de dirección es igual a cero. Para ello, tomamos un punto genérico que pertenezca a la recta r, definido por las ecuaciones paramétricas de la recta y con ese punto, cuyas coordenadas estarán en función de un parámetro «t», calculamos el vector PP’.

Al realizar el producto escalar del vector PP’  con el vector de dirección de la recta e igualarlos a cero, tendremos una ecuación donde podremos despejar el valor de «t» y finalmente, calcular las coordenadas del punto P’ que estamos buscando.

Vamos a ver un ejemplo:

Ejercicio resuelto sobre cálculo de la proyección de un punto sobre una recta

Calcula la proyección ortogonal del punto P (1,2,3) sobre la la siguiente recta:

Tenemos el siguiente punto:

Y queremos calcular la proyección ortogonal sobre la recta:

Cuyo vector de dirección es:

Ahora vamos calcular el vector PP’. Pala ello, obtenemos las ecuaciones paramétricas de la recta:

Cada una de las ecuaciones paramétricas de la recta, corresponde a una coordenada de un punto genérico de la recta, es decir, un punto que pertenezca a la recta. Por tanto el punto P’ tendría las siguientes coordenadas, que dependen del parámetro «t»:

Con este punto P’, calculamos las coordenadas del vector PP’, restando las coordenadas del extremo menos las coordenadas del origen:

Ya tenemos ambos vectores: PP’ y el vector de dirección v. Como son perpendiculares, su producto escalar es igual a cero:

Sustituimos cada vector por sus coordenadas en la expresión anterior:

En el primer miembro de la ecuación realizamos el producto escalar mediante su expresión analítica, sumando las multiplicaciones de las coordenadas de ambos vectores:

Nos queda una ecuación de primer grado que depende de «t».

Reagrupamos términos semejantes:

Y despejamos t:

El valor de t obtenido, lo sustituimos en las coordenadas del punto P’ que teníamos en función de t:

Y finalmente, operando en cada coordenada, obtenemos las coordenada del punto P’, que es la proyección del punto P sobre la recta r:

Proyección de una recta sobre un plano

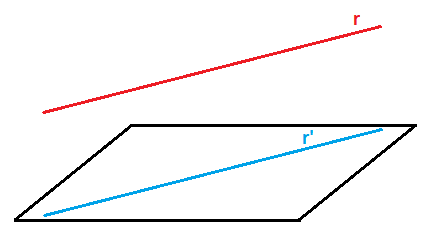
La proyección de una recta sobre un plano es una recta contenida en dicho plano y está determinada por la proyección de los puntos que pertenecen a la recta r sobre el plano:

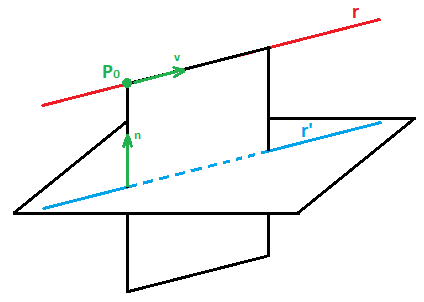
Al mismo tiempo, la recta r es la intersección del plano que contiene a la recta r y es perpendicular al plano dado:

Para calcular la proyección de una recta sobre un plano, debemos empezar calculando el plano que contiene a la recta r y es perpendicular al plano dado. Este plano estará definido por un punto que pertenezca a la recta y dos vectores, que son el vector de dirección de la recta y el vector normal al plano.

Una vez tenemos este plano, tenemos que calcular la recta intersección entre ambos planos, que será la proyección de la recta que estábamos buscando.

Vamos a ver un ejemplo:

Ejercicio resuelto sobre cálculo de la proyección de una recta sobre un plano

Calcular la proyección de la siguiente recta:

Sobre el siguiente plano:

En primer lugar calculamos el plano que contiene a la recta r y es perpendicular al plano. Para ello necesitamos conocer el vector de dirección de la recta, el vector normal al plano y un punto que pertenezca a la recta r:

Empezamos calculando el vector de dirección de la recta. Como la ecuación de la recta está en forma implícita, el vector de dirección se calcula como el producto vectorial de los vectores normales de cada plano que la definen:

Por lo que el vector de dirección de la recta es:

Ahora vamos a calcular un punto P0 que pertenezca a la recta. Para ello, vamos a establecer por ejemplo que el valor de z sea 0. Al ser z=0, las ecuaciones de la recta nos quedan de la siguiente manera:

Es decir, no queda un sistema de 2 ecuaciones con 2 incógnitas, que podemos resolver y obtener los valores de «x» e «y», que son:

Por tanto, las coordenadas del punto P0 que pertenece a la recta son:

El vector normal al plano lo obtenemos directamente del plano dado:

Ya tenemos los dos vectores y el punto que necesitamos para obtener el plano:

Con estos datos, obtenemos las ecuaciones paramétricas del plano, que tienes explicado cómo hacerlo más paso a paso en la lección de las ecuaciones del plano:

Ahora pasamos las ecuaciones paramétricas del plano a las ecuaciones implícitas. Para ello, consideramos t y s como las incógnitas y «x», «y» y «z» pasan a ser términos independientes:

Debemos resolver este sistema.

La matriz de los coeficientes es:

Y la matriz ampliada:

En este caso, tanto el rango de A es igual a 2, ya la mayor submatriz de orden 2 es igual a cero (puedes calcularlo para comprobarlo).

Tenemos que forzar a que el sistema tenga solución, luego el rango de la matriz ampliada también debe ser igual a 2, para que de esta forma el sistema sea compatible determinado y tenga solución:

Para que el rango de la matriz ampliada sea igual a 2:

El determinante debe ser igual a cero:

Desarrollando el determinante, operando y reordenando términos nos queda la siguiente ecuación implícita del plano:

Que junto con la ecuación del plano que ya teníamos forman las ecuaciones implícitas de la recta r’, que es la proyección de la recta r sobre el plano:

Tienes explicado paso a paso en el Curso de Geometría Analítica en el Espacio, como pasar de las ecuaciones paramétricas a las implícitas o cómo desarrollar el determinante mediante la regla de Sarrus.

¿Necesitas ayuda en matemáticas? ¿Quieres que te explique cualquier duda que te surja?

Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.

He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.

Con mi método:

• Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
• Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión

Suena bien ¿no?

¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?

Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más:

ENSÉÑAME MATEMÁTICAS