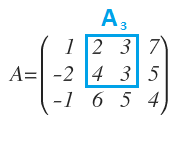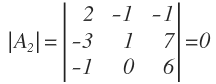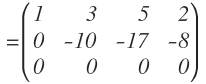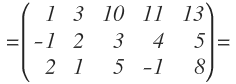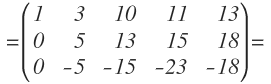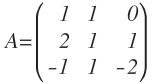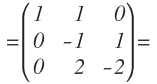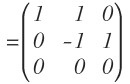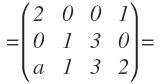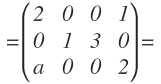Qué es y cómo calcular el Rango de una Matriz por determinantes y por Gauss. Ejercicios resueltos.

En esta lección te voy a explicar qué es el rango de una matriz y cómo calcular el rango de una matriz por determinantes y por el método de Gauss. Aprenderás a calcular el rango de cualquier matriz, tanto cuadrada como no cuadrada.

Si has llegado hasta aquí es porque necesitas un profesor de matemáticas online. Si después de leer esto, quieres que te ayude a entenderlas de verdad, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.

Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:

QUIERO APRENDER MATEMÁTICAS

Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.

Qué es el rango de una matriz

El rango de una matriz se puede definir de dos formas. Vamos con la primera definición y más abajo veremos la segunda:

El rango de A se escribe como Rag A o rg(A).

Vamos a ver esta definición un poco más despacio.

En primer lugar, el orden de una matriz cuadrada es el número de filas o de columnas que tiene esa matriz. Por ejemplo, una matriz de orden 2, es lo mismo que decir una matriz de dimensiones 2×2, que tiene 2 filas y 2 columnas.

Por otro lado, se le llama submatriz, a una matriz que está contenida dentro de otra matriz. Dentro de una matriz, podemos elegir filas y columnas que formen otra matriz independiente.

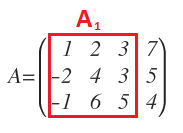
Por ejemplo, en la siguiente matriz de dimensiones 3×4:

Puedo elegir las siguientes filas y columnas dentro de A:

Que forman la siguiente submtariz cuadrada de orden 3:

O incluso puedo elegir columnas que no estén seguidas:

Y tendría otra submatriz cuadrada de orden 3:

O puedo elegir menos filas y columnas:

Que formarían una matriz cuadrada de orden 2:

Para calcular el rango de una matriz, debemos elegir la submatriz de mayor orden posible y calcular su determinante.

El orden de la mayor submatriz cuadrada, cuyo determinante sea distinto de cero, será el rango de la matriz.

Vamos a ver un ejemplo en el siguiente apartado.

Cómo calcular el rango de una matriz no cuadrada por determinantes

Como veremos a continuación, se puede obtener el rango de cualquier matriz, sin necesidad de que sea cuadrada.

¿Cuál es el rango de la siguiente matriz?

Es una matriz de dimensiones 3×4, por lo que no es una matriz cuadrada.

Tenemos que elegir la mayor submatriz cuadrada que esté contenida en A para calcular su determinante, que es de orden 3.

Calcularemos los determinantes de todas las posibles submatrices cuadradas de orden 3, hasta encontrar una cuyo determinante sea distinto de 0. Basta con encontrar al menos una submatriz cuadrada de orden 3, cuyo determinante sea distinto de 0, para que el rango de la matriz A sea 3.

Elegimos esta submatriz cuadrada:

Y calculamos su determinante:

Su resultado es distinto de cero, por tanto, como el orden de esta submatriz es 3, el rango de la matriz A es 3

Si todos los determinantes de las submatrices de orden 3 fueran igual a cero, tendríamos que seguir con las submatrices de orden 2, hasta encontrar un determinante que fuera distinto de 0 y en ese caso, el rango de la matriz sería 2.

Vamos a ver otro ejemplo: Calcular el rango de la siguiente matriz:

Las mayores submatrices cuadradas, contenidas en A, que podemos elegir son de orden 3. Vamos a ir calculando los determinantes de todas las posibles submatrices cuadradas de orden 3, hasta encontrar una cuyo determinante sea distinto de 0.

Empezamos eligiendo la submatriz cuadrada formada por las tres primeras columnas:

Su determinante es cero, por lo que tenemos que seguir buscando.

Probamos con la submatriz cuadrada formada por las columnas 2, 3 y 4:

Su determinante es cero. Tenemos que seguir buscando.

Elegimos la submatriz cuadrada formada por las columnas 1, 2 y 4:

Su determinante también es cero.

Y por último, elegimos la submatriz cuadrada formada por las columnas 1, 3 y 4:

Que su determinante también es cero.

Ya no quedan más combinaciones de columnas para seguir eligiendo submatrices cuadradas de orden 3. Todas las submatrices cuadradas de orden 3, que están contenidas en A son igual a cero, por tanto, el rango de A, va a ser menor que 3:

Al no encontrar ninguna submatriz cuadrada de orden 3, cuyo determinante sea distinto de cero, vamos a probar con con submatrices cuadradas de orden 2.

Basta encontrar una cuyo determinante sea distinto de cero.

Probamos con la submatriz cuadrada de orden 2, formada por las columnas 1 y 2 y por las filas 1 y 2:

Su resultado es distinto de cero, por tanto el rango de la matriz es 2:

Que coincide con el orden de la mayor submatriz cuadrada que hemos encontrado, cuyo determinante es distinto de cero.

Cómo calcular el rango de una matriz cuadrada por determinantes

Calcular el rango de una matriz cuadrada es algo más sencillo, ya que para empezar, no tenemos que estar buscando la mayor submatriz cuadrada, al ser la propia matriz.

Sin embargo, si la matriz es de orden 4 o mayor, si que tenemos varias submatrices de orden 3 o menor para elegir que estén contenidas en la matriz principal.

Por ejemplo: ¿Cuál es el rango de la siguiente matriz cuadrada?

La mayor submatriz cuadrada que podemos elegir es la misma matriz, por lo que empezamos calculando su determinante:

Que es distinto de cero, por lo que el rango de la matriz A, es de rango 4, que coincide con su orden:

Veamos un último ejemplo: Calcular el rango de la siguiente matriz:

Empezamos calculando el determinante de la matriz, ya que es la mayor submatriz cuadrada:

Su determinante es igual a cero. Como no podemos elegir más submatrices de orden 4, el rango de B va a ser menor que 4:

Buscaremos por tanto una submatriz cuadrada de orden 3, que esté contenida en B, cuyo determinante sea distinto de cero. Sólo con que encontremos una, el rango de B, ya será igual a 3.

Elegimos la submatriz cuadrada de orden 3 formada por las columnas 1, 2 y 3 y las filas 1, 2 y 3. Calculamos su determinante:

Su determinante es distinto de cero, luego ya no tenemos que seguir buscando y el rango de B es 3:

Vamos a ver ahora cómo calcular el rango de una matriz por el método de Gauss y para ello, antes debemos saber qué son los vectores linealmente independientes:

Qué son los vectores linealmente independientes

Los vectores linealmente independientes son los vectores cuya formación no depende de ningún otro vector de la matriz, es decir, que no se puede componer a partir de la composición lineal del resto de vectores.

Los vectores linealmente de una matriz es el número de vectores distintos de cero que quedan después de haber triangulado la matriz formada por ellos.

Vamos a ver un ejemplo:

¿Cuántos vectores linealmente independientes tiene la siguiente matriz?

Para empezar, los vectores de una matriz a los que nos referimos son los vectores fila, es decir, que cada fila de la matriz corresponde a un vector:

Para obtener el número de vectores linealmente independientes, vamos a triangular la matriz, es decir, vamos a hacer que los elementos que quedan por debajo de la diagonal principal sean ceros.

El primer elemento de la primera columna ya es 1. Sólo nos falta que los elementos que quedan por debajo de ese 1 sean ceros.

Para conseguirlo, a la fila 2 le restamos 4 veces al fila 1 y dejamos el resultado en la fila 2:

Y a la fila 3 le restamos 3 veces la fila 1, dejando el resultado en la fila 3:

La matriz queda:

Sólo nos queda que el último elemento de la segunda columna sea cero. Por tanto, a la fila 3 le restamos la fila 2 y dejamos el resultado en la fila 3:

Nos queda:

Nos ha quedado una fila llena de ceros. Por tanto, esta matriz tiene dos vectores linealmente independientes y como consecuencia, el otro vector es dependiente de los otros dos.

Los vectores V1 y V2 son independientes:

El vector V3, que es el que nos ha quedado con ceros, depende de V1 y V2. De hecho, podemos formar el V3 restando V2 menos V1, o lo que es lo mismo, la fila 3 es igual a la fila 2 menos la fila 1:

Rango de una matriz por el método de Gauss

¿Qué es el rango de una matriz?

Al principio vimos una de las definiciones. Vamos ahora con la segunda definición:

Por tanto, calcular el número de vectores linealmente independientes y calcular el rango de la matriz es exactamente lo mismo. Así que, el rango de la matriz anterior es 2, ya que es el número de vectores linealmente que tiene:

También se puede calcular el rango de una matriz por determinantes como hemos visto anteriormente.

Vamos a ver otro ejemplo de cómo calcular el rango de una matriz por Gauss:

¿Cuál es el rango de la siguiente matriz?

Vamos a empezar a triangula la matriz, para ello, en el primer elemento de la primer columna, tenemos que hacer que haya un 1. Lo conseguimos si intercambiamos al fila 3 por la fila 1:

La matriz queda:

Ahora tenemos que que hacer que los elementos que quedan por debajo de 1 en la primera columna sean ceros. Para ello a la fila 2 le sumamos la fila 1 y el resultado lo dejamos en la fila 2:

Y a la fila 3 le restamos dos veces la fila 1, dejando el resultado en la fila 3:

La matriz nos queda de la siguiente manera:

Lo siguiente que tenemos que conseguir es que el último elemento de la segunda columna sea un cero. Para ello, a la fila 3 le sumamos la fila 2, dejando el resultado en la fila 3:

La matriz queda:

Ya hemos triangulado la matriz y no nos ha quedado ninguna fila con ceros, luego los 3 vectores de la matriz son linealmente independientes. Por tanto, como la matriz tiene 3 vectores linealmente independientes, su rango es 3:

Si quieres seguir aprendiendo cómo operar con matrices, cómo calcular la inversa de una matriz o cómo resolver ecuaciones matriciales, te aconsejo mi Curso de Matrices, donde lo tienes explicado al detalle, con ejercicios resueltos paso a paso.

Ejercicios resueltos sobre calcular el rango de una matriz por el método de Gauss

Vamos a realizar un par de ejercicios sobre cómo calcular el rango de una matriz.

Ejercicio 1

Calcular el rango de la siguiente matriz:

Como ya sabes, debemos triangular la matriz.

Ya tenemos un 1 en el primer elemento de la primera columna, por lo que debemos hacer que el resto de elementos de esa columna sean ceros.

Lo conseguimos restando a la fila 2 dos veces la fila 1 y dejando el resultado en la fila 2:

Y sumando la fila 1 a la fila 3 y el resultado lo dejamos en la fila 3:

La matriz queda:

Nos queda hacer cero el último elemento de la segunda columna y para conseguirlo, a la fila 3 le sumamos dos veces la fila 2, dejando el resultado en la fila 3:

La matriz nos queda:

Tenemos  una fila con ceros, luego quiere decir que tenemos 2 vectores linealmente independientes. Por tanto, el rango de la matriz es 2:

En los casos que hemos resuelto aquí, al triangular la matriz nos quedan 2 ceros en la primera columna y 1 cero en la segunda columna, ya que las matrices tenían 3 filas. Recuerda que triangular la matriz es hacer ceros debajo de la diagonal principal y que en cada caso será distinto, en función del número de filas de la matriz.

Como ves, el procedimiento para calcular el rango de una matriz es siempre el mismo. El siguiente ejercicio es un poco distinto, lo cual te permitirá entender también un poco más este concepto.

Ejercicio 2

Calcula el rango de la siguiente matriz según el valor de «a»:

En este ejercicio debemos decir cuál es el rango de la matriz, en función de los valores que pueda tomar «a». Pero no hay que calcular el rango de la matriz para los infinitos valores que puede tomar «a». Tan sólo nos interesa cuando el lugar que ocupa «a» sea cero o distinto de cero.

Vamos a verlo más despacio.

Para empezar, triangulamos la matriz como siempre. Para ello, hacemos cero el segundo elemento de la primera columna, restando la fila 1 a la fila 2 y dejando el resultado en la fila 2:

El tercer elemento de la primera columna, como tenemos el parámetro «a», lo dejamos como está. La matriz queda:

Seguimos triangulando la matriz haciendo cero el último elemento de la segunda columna. Para ello, a la fila 3 le restamos la fila 2 y dejamos el resultado en la fila 3:

La matriz queda:

En teoría, la matriz ya está triangulada. Digo en teoría, porque no tenemos un cero en el tercer elemento de la primera columna, sino que tenemos el parámetro «a».

Conforme está la matriz, no podemos llegar a ninguna conclusión, ya que el rango de la matriz sería 3 independientemente del valor de «a», ya que en el último elemento de la tercera fila tenemos un 2. Luego el valor de «a» no influye en el resultado.

Sin embargo, si el resto de elementos de la tercera fila fueran todo ceros, el valor de «a» sí que sería determinante. Antes de decirte por qué, vamos a hacer cero ese elemento.

A la fila 3 le restamos dos veces la fila 1. El resultado lo dejamos en la fila 3:

La matriz queda:

Ahora se ve más claro.

Si el elemento a-4 es igual a cero, de donde se obtiene a=4, la matriz tendría dos vectores linealmente independeintes, luego su rango sería 2:

Para cualquier otro valor de a que no fuera 4, es decir, que el elemento a-4 fuera distinto de cero, entonces la matriz tiene 3 vectores linealmente independientes y por tanto su ranto es 3:

¿Necesitas ayuda en matemáticas? ¿Quieres que te explique cualquier duda que te surja?

Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.

He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.

Con mi método:

• Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
• Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión

Suena bien ¿no?

¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?

Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más:

ENSÉÑAME MATEMÁTICAS