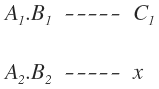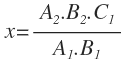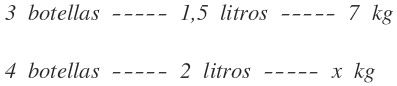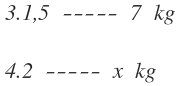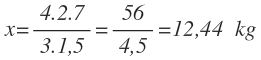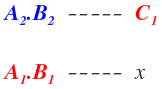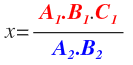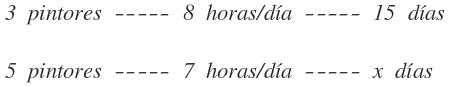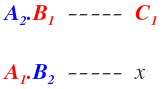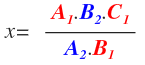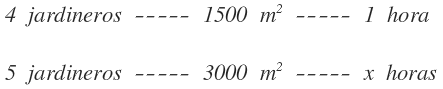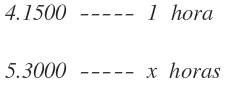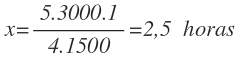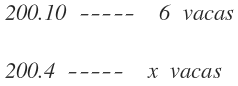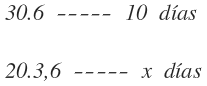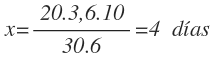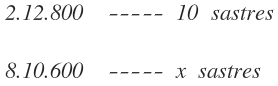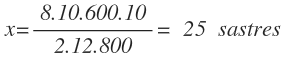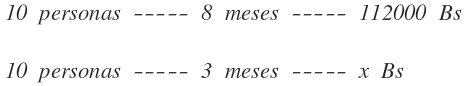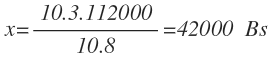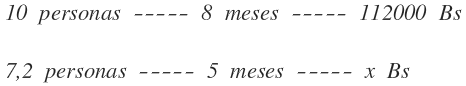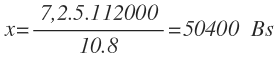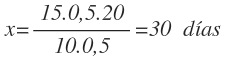En esta lección te voy a explicar cómo se hace una regla de tres compuesta directa e inversa y cuándo debes utilizarla, con ejercicios resueltos paso a paso.
Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Regla de tres compuesta
¿Qué es una regla de tres compuesta y cuándo se utiliza?
En primer lugar, vamos a ver qué es una regla de tres compuesta, a partir de lo que conocemos de una regla de tres simple.
En una regla de tres simple, están relacionadas dos magnitudes y calculamos una cantidad desconocida a partir de otras tres cantidades conocidas.
Una regla de tres compuesta se utiliza cuando hay implicadas más de dos magnitudes, y queremos calcular una cantidad desconocida de una de esas magnitudes, como por ejemplo en este problema:
Para cortar el césped de una parcela de 1500 m², se necesitan 5 jardineros trabajando durante 1 hora. ¿Cuánto tardarán 4 jardineros en cortar el césped de otra parcela de 3000 m²?
En este problema están implicadas tres magnitudes, como son:
- El área de la parcela
- El número de jardineros
- El tiempo
Por tanto, para resolver este problema, tenemos que utilizar una regla de tres compuesta.
Entre las magnitudes pueden existir relaciones de proporcionalidad directa o inversa, por lo que las reglas de tres pueden ser: regla de tres compuesta directa, regla de tres compuesta inversa y regla de tres compuesta mixta.
Vamos a ir viendo cada una de ellas.
Regla de tres compuesta directa
La regla de tres compuesta directa es aquella en la que las magnitudes tienen una relación directamente proporcional con la magnitud de la que desconocemos uno de sus valores.
Recordamos que dos magnitudes son directamente proporcionales cuando al aumentar una, aumenta la otra o cuando al disminuir una, disminuye la otra.
Por ejemplo, si tenemos 3 magnitudes implicadas A, B y C, donde desconocemos uno de los valores de la magnitud C, para que la regla de tres compuesta sea directa A y C deben ser directamente proporcionales y por otro lado, B y C también deben ser directamente proporcionales.
Cómo resolver una regla de tres compuesta directa
Para resolver la regla de tres compuesta directa, colocamos en la primera columna de la regla de tres los valores de una de las dos magnitudes que conozcamos todas sus valores, por ejemplo de la magnitud A, en la segunda columna, los valores de la otra magnitud que conocemos, por ejemplo de la magnitud B y en la última columna, el valor que conocemos de C y el valor que no conocemos de C al que llamaremos x:
En las dos primeras columnas da igual si colocamos A o B en cualquiera de ellas. Lo que sí es obligatorio es colocar la magnitud sobre la que desconocemos uno de sus valores en la última columna.
Ahora multiplicamos en línea los valores de las magnitudes que si conocemos y dejamos el resultado en una sola columna, quedando:
Tenemos ahora una regla de tres simple directa, donde x será igual a la fracción cuyo numerador estará formado por la multiplicación de las cantidades que están en la diagonal opuesta a la x y cuyo denominador la formará la cantidad que está en al misma diagonal que la x:
Ejemplo resuelto de regla de tres compuesta directa
Vamos a ver un ejemplo de cómo hacer una regla de tres compuesta directa:
Para una manualidad, hemos llenado de arena 3 botellas de plástico de 1,5 litros y entre todas pesan 7 kg. ¿Cuánto pesarán 4 botellas de 2 litros?
El primer paso es identificar las magnitudes implicadas en el problema, que son:
- Número de botellas
- Capacidad de las botellas (litros)
- Peso de todas las botellas (kg)
Ahora tenemos que identificar la relación de proporcionalidad de la magnitud de la que desconocemos uno de sus valores con las otras dos, es decir, entre el peso de las botellas con el número de botellas y entre el peso de las botellas con la capacidad de las botellas.
Relación de proporcionalidad entre el peso de las botellas y el número de botellas
Si aumento el número de botellas, el peso de las botellas también aumenta y si disminuyo el número de botellas, el peso disminuye, por lo que estas dos magnitudes son directamente proporcionales.
Relación de proporcionalidad entre el peso de las botellas y la capacidad de las botellas
Si aumento la capacidad de botellas, el peso de las botellas también aumenta y si disminuyo la capacidad de las botellas, el peso disminuye, por lo que estas dos magnitudes también son directamente proporcionales.
En la primera columna colocamos las botellas, en la segunda columna los litros y en la última columna los kilos, que es la magnitud donde me falta por saber uno de sus valores:
Ahora multiplico en línea los valores de las dos primeras columnas, dejando el resultado en una sola columna:
Finalmente, calculo la x, como la multiplicación de los valores que están en la diagonal opuesta a la x, entre el valor que está en su misma diagonal:
Por tanto, 4 botellas de 2 litros pesarán 12,44 kg
Regla de tres compuesta inversa
La regla de tres compuesta inversa es aquella en la que las magnitudes tienen una relación inversamente proporcional con la magnitud de la que desconocemos uno de sus valores.
Dos magnitudes son inversamente proporcionales cuando al aumentar una, disminuye la otra o cuando al disminuir una, aumenta la otra.
Por ejemplo, si tenemos 3 magnitudes implicadas A, B y C, donde desconocemos uno de los valores de la magnitud C, para que la regla de tres compuesta sea inversa A y C deben ser inversamente proporcionales y por otro lado, B y C también deben ser inversamente proporcionales.
Cómo resolver una regla de tres compuesta inversa
Para resolver la regla de tres compuesta inversa, colocamos en la primera columna los valores de una de las dos magnitudes que conozcamos todas sus valores, por ejemplo de la magnitud A, en la segunda columna, los valores de la otra magnitud que conocemos, por ejemplo de la magnitud B y en la última columna, el valor que conocemos de C y el valor que no conocemos de C al que llamaremos x:
Al igual que pasaba con la regla de tres compuesta directa, en las dos primeras columnas da igual si colocamos la magnitud A o la magnitud B en cualquiera de ellas. Lo que sí es obligatorio es colocar la magnitud de la que desconocemos uno de sus valores en la última columna.
Ahora invertimos el orden a los valores de las magnitudes, es decir, los valores que están abajo los ponemos arriba y viceversa: A2 lo ponemos arriba y A1 abajo y con B2 y B1 hacemos lo mismo. La regla de tres queda de la siguiente forma:
Ahora multiplicamos en línea los valores de las magnitudes que si conocemos, tal y como los tenemos ahora y dejamos el resultado en una sola columna, quedando:
Calculamos x igual que siempre, que será igual a la fracción cuyo numerador estará formado por la multiplicación de las cantidades que están en la diagonal opuesta a la x y cuyo denominador la formará la cantidad que está en al misma diagonal que la x:
La diferencia de la regla de tres compuesta inversa con la regla de tres compuesta directa es que en la primera hemos invertido el orden de los valores de las magnitudes.
Ejemplo resuelto de regla de tres compuesta inversa
Vamos a ver un ejemplo de cómo hacer una regla de tres compuesta inversa:
3 pintores tardan 15 días en pintar una nave industrial, trabajando 8 horas diarias. ¿Cuántos días tardarán 5 pintores trabajando 7 horas diarias?
Identificamos las magnitudes implicadas en el problema:
- Número de pintores
- Número de días
- Número de horas diarias
Ahora tenemos que identificar la relación de proporcionalidad de la magnitud de la que desconocemos uno de sus valores con las otras dos, es decir, entre el número de días con el número de pintores y entre el número de días con el número de horas diarias.
Relación de proporcionalidad entre el número de días y el número de pintores
Si aumento el número de pintores, el número de días que tardan en pintar disminuye y si disminuyo el número de pintores, el número de días aumenta, por lo que estas dos magnitudes son inversamente proporcionales.
Relación de proporcionalidad entre el número de días y el número de horas diarias
Si aumento el número de horas diarias, el número de días que tardan en pintar disminuye y si disminuyo el número de horas diaria, el número de días aumenta, por lo que estas dos magnitudes también son inversamente proporcionales.
En la primera columna colocamos el número de pintores, en la segunda columna el número de horas diarias y en la última columna el número de días, que es la magnitud donde me falta por saber uno de sus valores:
Invertimos los valores de las magnitudes, es decir, el 5 de los pintores pasa arriba y el 3 abajo y el 7 de las horas/día pasa arriba y el 8 abajo:
Multiplico en línea los valores que me quedan en las dos primeras columnas:
Y por último calculo la x, como la multiplicación de los valores que están en la diagonal opuesta a la x, entre el valor que está en su misma diagonal:
5 pintores trabajando 7 horas diarias tardarán 10,28 días.
Regla de tres compuesta mixta
La regla de tres compuesta mixta es aquella donde se combina que las magnitudes implicadas tienen una relación directamente proporcional e inversamente proporcional con la magnitud de la que desconocemos uno de sus valores.
Por ejemplo, si tenemos 3 magnitudes implicadas A, B y C, donde desconocemos uno de los valores de la magnitud C, para que la regla de tres compuesta sea mixta, por ejemplo A y C deben ser inversamente proporcionales y por otro lado, B y C deben ser directamente proporcionales. (Puede ser también al contrario)
Cómo resolver una regla de tres compuesta mixta
Para resolver la regla de tres compuesta mixta, colocamos en la primera columna los valores de una de las dos magnitudes que conozcamos todas sus valores, por ejemplo de la magnitud A, en la segunda columna, los valores de la otra magnitud que conocemos, por ejemplo de la magnitud B y en la última columna, el valor que conocemos de C y el valor que no conocemos de C al que llamaremos x:
Ahora invertimos el orden a los valores de las magnitudes inversamente proporcionales, es decir, en este caso A y C son inversamente proporcionales, por lo que el valor A2 lo ponemos arriba y el valor A1 abajo. La regla de tres queda de la siguiente forma:
Ahora multiplicamos en línea los valores que nos quedan de las magnitudes que si conocemos y dejamos el resultado en una sola columna, quedando:
Finalmente calculamos x igual que siempre, que será igual a la fracción cuyo numerador estará formado por la multiplicación de las cantidades que están en la diagonal opuesta a la x y cuyo denominador la formará la cantidad que está en al misma diagonal que la x:
Date cuenta que este valor de x es así porque las magnitudes A y C son inversamente proporcionales. El valor de x dependerá en cada caso de las magnitudes directa e inversamente proporcionales que existan.
Ejemplo resuelto de regla de tres compuesta mixta
Vamos a ver un ejemplo de cómo hacer una regla de tres compuesta mixta y para ello utilizaremos el problema que utilizamos en el primer ejemplo:
Para cortar el césped de una parcela de 1500 m², se necesitan 5 jardineros trabajando durante 1 hora. ¿Cuánto tardarán 4 jardineros en cortar el césped de otra parcela de 3000 m²?
Como sabemos, en este problema están implicadas tres magnitudes:
- El área de la parcela
- El número de jardineros
- El tiempo
Queremos calcular el tiempo, luego el primer paso es identificar qué relación de proporcionalidad existe entre las otras dos magnitudes y el tiempo, es decir, entre el tiempo con el área de la parcela y el tiempo con el número de jardineros.
Relación de proporcionalidad entre el tiempo y el área de la parcela
Si el área de la parcela aumenta, el tiempo en cortar el césped también aumenta y si el área de la parcela disminuye, el tiempo que se necesita también disminuye, luego estas dos magnitudes son directamente proporcionales.
Relación de proporcionalidad entre el tiempo y el número de jardineros
Si aumento el numero de jardineros, el tiempo que se necesita en cortar el césped disminuye y si disminuyo el número de jardineros, se necesita más tiempo, por lo que estas dos magnitudes también son inversamente proporcionales.
En la primera columna colocamos el número de jardineros, en la segunda columna el tamaño de la parcela y en la última columna el tiempo, que es la magnitud donde me falta por saber uno de sus valores:
Invertimos el orden los valores de las magnitudes inversamente proporcionales, es decir, los valores del número de jardineros, el 4 pasa arriba y el 5 abajo:
Multiplico en línea los valores que me quedan en las dos primeras columnas:
Y por último calculo la x, como la multiplicación de los valores que están en la diagonal opuesta a la x, entre el valor que está en su misma diagonal:
Ejercicios resueltos de regla de tres compuesta
Ejercicio 1
Un grupo de 20 trabajadores debe ordeñar seis vacas en 10 días. Luego de 4 días, se les unen 5 personas doblemente eficientes. ¿Cuántos días tardarán en ordeñar todas las vacas?
En primer lugar, vamos a calcular el número de vacas que ordeñan 20 trabajadores en 4 días. Sabemos que 20 trabajadores tardan 10 días en ordeñar 6 vacas. En la primera columna colocamos a los trabajadores, en la segunda los días y en la tercera el número de vacas, que es la magnitud que desconocemos:
Comparamos los trabajadores y los días con las vacas, para saber si son directa o inversamente proporcionales:
Trabajadores VS Vacas: Directamente proporcionales ya que con más trabajadores se pueden ordeñar más vacas y con menos trabajadores menos vacas.
Días VS Vacas: Directamente proporcionales ya que con más días se pueden ordeñar más vacas y con menos días menos vacas.
No es necesario invertir el orden de ninguna magnitud, por lo que multiplicamos en línea las magnitudes de las dos primeras columnas:
Y despejamos y resolvemos la x:
Por tanto, los primeros 4 días, ordeñaron 2,4 vacas y por tanto, les quedan 3,6 vacas por ordeñar:
En ese momento se unen a ellos 5 trabajadores el doble de eficientes, es decir, que cada uno de esos trabajadores vale por 2, por lo que en total es equivalente a tener 30 trabajadores:
Ahora vamos a calcular cuántos días tardan en ordeñar 3,6 vacas esos 30 trabajadores, partiendo que sabemos que 20 trabajadores ordeñan 6 vacas en 10 días.
En la primera columna colocamos los trabajadores, en la segunda las vacas y en la tercera los días, que es donde tenemos la incógnita:
Comparamos los trabajadores y las vacas con los días, para saber si son directa o inversamente proporcionales:
Trabajadores VS Días: Inversamente proporcionales ya que con más trabajadores se necesitan menos días y con menos trabajadores se necesitan más días
Vacas VS Días: Directamente proporcionales ya que para ordeñar más vacas se necesitan más días y si tenemos menos vacas necesitamos menos días.
Por tanto, invertimos el orden de los trabajadores:
Multiplicamos en línea las magnitudes de las dos primeras columnas:
Y despejamos y resolvemos la x:
Por tanto, el equivalente a 30 trabajadores, tardan 4 días en ordeñas 3,6 vacas, que sumados a los 4 días que ya llevaban, hacen un total de 8 días:
Ejercicio 2
10 sastres trabajando 8 horas diarias durante 10 días, confeccionan 800 trajes. ¿Cuántos sastres de igual rendimiento lograrán confeccionar 600 trajes trabajando 2 horas diarias durante 12 días?
Colocamos en la primer columna las horas diarias, en la segunda los días, en la tercera los trajes y en la cuarta los sastres:
Ahora comparamos cada una de las magnitudes con los sastres para saber su razón de proporcionalidad:
Horas diarias VS Sastres: Inversamente proporcional, ya que si trabajan más horas al día, harán falta menos sastres y si trabajan menos horas, se necesitarán más sastres.
Días VS Sastres: Inversamente proporcional, ya que cuantos más días se tengan, se necesitan menos sastres para confeccionar el mismo número de trajes y viceversa.
Trajes VS Sastres: Directamente proporcional, porque para hacer más trajes hacen falta más sastres y para hacer menos trajes hacen falta menos sastres .
Invertimos el orden de las horas diarias y de los días, que son las magnitudes inversamente proporcionales:
Y multiplicamos en línea las magnitudes de las tres primeras columnas:
Finalmente despejamos y calculamos la x:
Ejercicio 3
Una familia de 10 personas cuenta con Bs 112 000 para vivir 8 meses en una ciudad. A los 3 meses, mueren 4 de sus integrantes y el costo de vida aumenta en 1/5. ¿Cuánto dinero sobrará después de los 8 meses?
Primero vamos a calcular cuánto dinero gastan 10 personas en 3 meses.
Para ello, colocamos las personas en la primera columna, los meses en la segunda y los Bs en la tercera, por ser la magnitud que desconocemos:
Ahora comparamos las personas y los meses con los Bs para saber su razón de proporcionalidad:
Peronsas VS Bs: Directamente proporcional, ya que a más personas, necesitan más Bs y viceversa
Meses VS Bs: Directamente proporcional, ya que a más meses, se necesitan más Bs y viceversa
Por tanto, no invertimos ninguna magnitud y multiplicamos en línea las dos primeras columnas:
Ahora despejamos y calculamos x:
Por tanto, en 3 meses, 10 personas gastan 42000 Bs.
A partir de aquí, tenemos 4 personas menos (quedan 6) y de las que quedan, el nivel de vida aumenta 1/5, es decir hay que sumar 6 veces 1/5. Operamos y nos queda:
Ahora vamos a calcular el dinero que gastan el equivalente a esas 7,2 personas en los 5 meses que quedan:
Multiplicamos en línea las dos primeras columnas:
Y despejamos y calculamos la x:
7,2 personas gastan 50400 Bs en 5 meses.
Por tanto, a los 112000 que tenía en un principio, le resto 42000 que gastaron en los primeros 3 meses y los 50400 de los otros 5 meses y me quedan 19600 Bs:
Ejercicio 4
15 obreros han hecho la mitad de un trabajo en 20 días. En ese momento abandonan el trabajo 5 obreros. ¿Cuántos días tardarán en terminar el trabajo los obreros que quedan?
Coloco los obreros en la primera columna, el trabajo en la segunda columna y los días en la tercera columna:
Comparamos los obreros y el trabajo con los días:
Obreros VS Días: Inversamente proporcional, ya que a más trabajadores, se necesitan menos días y viceversa
Trabajo VS Días: Directamente proporcional, ya que a más trabajo se necesitan más días y viceversa.
Invertimos el orden de los obreros por ser inversamente proporcional:
Multiplicamos en línea las dos primeras columnas:
Y despejamos y calculamos la x:
Por tanto, los 10 obreros que quedan tardan en terminar el trabajo otros 30 días.
¿Necesitas ayuda con las matemáticas? ¿Quieres que te explique cualquier duda que te surja paso a paso?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: