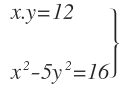A continuación vamos a ver cómo resolver sistemas de ecuaciones de segundo grado, es decir, cuando al menos una de las incógnitas está elevada al cuadrado. Con ejercicios resueltos paso a paso.
¡Empezamos!
Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Cómo resolver sistemas de ecuaciones de segundo grado
En este tipo de sistemas, se utiliza el método de sustitución.
Estos sistemas de ecuaciones no son lineales, ya que las ecuaciones pueden aparecer elevadas al cuadrado, o bien las incógnitas pueden estar multiplicándose entre sí.
Debemos empezar despejando una incógnita que no esté elevada a ningún exponente, ya que de no hacerlo así, complicaríamos mucho los cálculos a realizar. Si no hubiera ninguna, no tenemos más remedio que despejar una incógnita elevada al cuadrado.
La expresión obtenida, la sustituimos en la ecuación que no hayamos utilizado y operamos. Dependiendo de cada caso, nos quedará una ecuación de segundo grado o mayor, que debemos resolver por con su método correspondiente.
En función del grado de la ecuación, se obtendrán dos o más soluciones para una de las incógnitas, las cuales debemos sustituir en la expresión donde despejamos la otra incógnita.
De esta forma, obtendremos varios pares de soluciones (x,y) del sistema de ecuaciones de segundo grado, que si lo representamos gráficamente, correspondería con el número de cortes entre ambas ecuaciones.
Puede que leyendo el método te haya resultado un poco confuso. Por eso, vamos a resolver algunos sistemas de ecuaciones de segundo grado paso a paso para que te quede más claro.
Ejercicios resueltos de sistemas de ecuaciones de segundo grado
Ejercicio resuelto 1
Vamos a resolver un sistema de ecuaciones de segundo grado, donde en la primera ecuación tenemos las incógnitas multiplicándose entre sí y en la segunda ecuación tenemos ambas incógnitas elevadas al cuadrado:
Empezamos despejando x de la primera ecuación ya que no está elevada a ningún exponente. Por tanto, en la primera ecuación:
Despejamos x:
En la segunda ecuación:
Sustituimos la x por la expresión que acabamos de obtener:
Y operamos para eliminar el paréntesis al cuadrado:
Reducimos todos los términos a común denominador:
Y finalmente eliminamos el denominador:
Pasamos todos los términos ordenados por grado a uno de los miembros, procurando que el primer término quede positivo dejando el otro miembro igual a cero:
Nos ha quedado una ecuación bicuadrada, o de cuarto grado. Para resolverla, debemos realizar el siguiente cambio de variable:
Realizamos el cambio de variable y nos queda:
Ahora calculamos t, como si se tratara de una ecuación de segundo grado completa:
Separamos el signo positivo del negativo para obtener las dos soluciones de t:
Una vez calculado el valor de t, deshacemos el cambio de variable para calcular el valor de «y»:
Para el primer valor de t, obtenemos dos valores de «y»:
Para el segundo valor de t, no obtenemos ningún valor de «y», ya que no tiene solución real:
Ahora volvemos a la expresión donde despejamos x:
Y sustituimos cada valor de «y» obtenido en esta expresión para calcular su correspondiente valor de x.
Para y=2 obtenemos el siguiente valor de x:
Para y=-2 obtenemos el siguiente valor de x:
Por tanto, el resultado de este sistema de ecuaciones de segundo grado son dos pares de soluciones:
Que también las podemos expresar de la siguiente forma:
Ejercicio resuelto 2
En este caso, tan solo la primera ecuación es no lineal, ya que tiene ambas incógnitas de segundo grado:
De segunda ecuación:
Despejamos «y» ya que no está multiplicada por ningún coeficiente y de esta forma no nos queda ningún denominador:
Ahora en la primera ecuación:
Sustituimos la «y» por la expresión obtenida anteriormente:
Desarrollamos el producto notable que nos queda:
Operamos y reordenamos términos:
Nos ha quedado una ecuación de segundo grado incompleta. Para resolverla, primero factorizamos:
De donde obtenemos que la primera solución es:
Y la segunda solución:
Cada uno de estos valores de x, los debemos sustituir en la expresión donde despejamos «y», para obtener su correspondiente valor de «y»:
Para x=0 tenemos:
Para x=4, obtenemos el siguiente valor de «y»:
Finalmente, estos son los dos pares de resultados que obtenemos del sistema de ecuaciones de segundo grado:
Que también las podemos expresar como:
Para saber resolver los sistemas de ecuaciones de segundo grado, además de dominar el método de sustitución, debes saber resolver tanto ecuaciones de segundo grado, como ecuaciones de tercer grado, como ecuaciones bicuadradas, además de saber aplicar los productos notables cuando sea necesario.
¿Necesitas ayuda en matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: